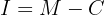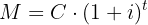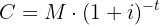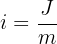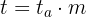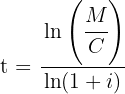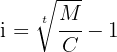Kapitel
Was sind Zinsen und wie werden sie berechnet?
Bei einigen Banken, Sparkonten oder auch bei Krediten und Pfandleihen wird ein monatlicher Zins erhoben. Das bedeutet nicht, dass dies bei allen Arten von Zinsen so ist.
Der Zeitraum, über den die Zinsen berechnet werden, kann jährlich, monatlich, wöchentlich oder sogar täglich sein.
Bei den in diesem Abschnitt vorgeschlagenen Übungen werden wir mit jährlichen Zinsen rechnen.
Darüber hinaus gibt es den einfachen Zins und den Zinseszins. In den Übungen, die wir uns ansehen werden, geht es um Zinseszinsen.
Formeln zur Berechnung von Zinseszinsen
Für die folgenden Formeln gilt die folgende Notation:
: Zins
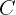: Startkapital
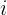: Zinssatz
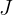: Nominalzinssatz
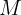: Endbetrag (oder zukünftiger Wert)
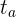: Zeitpunkt des Darlehens oder der Investition
: Laufzeit des Darlehens oder der Investition
: Häufigkeit der Kapitalisierung
So lauten die Formeln für die Berechnung von Zinseszinsen, wenn für den Zinssatz und die Zeit die gleiche Zeiteinheit verwendet wird, wie folgt:
Wenn Zeit und Zinsen in unterschiedlichen Einheiten angegeben werden, müssen wir vor der Anwendung der Formeln entsprechende Umrechnungen vornehmen.
Aufgaben zur Zinsrechnung
Wie lange muss ein Kapital von 25.000 € mit 5 % pro Quartal angelegt werden, damit es mit Zinseszins 30.387,66 € wird?
Wir stellen fest, dass wir das Sie, dass wir den Endbetrag, das Anfangskapital und den Zinssatz haben
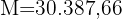
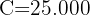
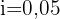vierteljährlich
Wir wenden die Formel direkt an, um die Zeit zu berechnen. Diese wird in Quartalen angegeben, wie der Zinssatz:
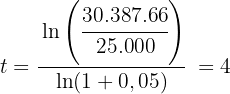
Daher beträgt die erforderliche Zeit vier Quartale.
Es werden 45.000 € mit Zinseszins geliehen, und nach 2 Jahren erhält man 52.488 €.
Berechne den Zinssatz.
Wir haben das Kapital, den Endbetrag und die Laufzeit der Investition
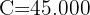
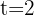Jahre
Wir wenden direkt die Formel zur Berechnung des Zinssatzes an
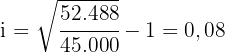
Der Zinssatz liegt bei 8 % pro Jahr.
Berechne den Zinseszinssatz (in Prozent), zu dem ein Kapitalbetrag geliehen werden muss, damit nach 20 Jahren die Zinsen dem geliehenen Kapitalbetrag entsprechen.
Wir möchten, dass die Zinsen dem Kapital entsprechen, also ist der Endbetrag doppelt so hoch wie das Kapital
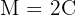
Wir stellen fest, dass wir den Endbetrag, das Kapital und die Laufzeit der Investition haben
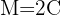
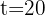
Da das Kapital nicht 0 ist, streichen wir 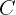von beiden Seiten der Gleichung für den Zinssatz und setzen den Investitionszeitraum ein:
Der Zinssatz liegt also bei 3,53 % jährlich.
Wie lange dauert es, bis der Zinseszins das Dreifache des Anfangskapitals bei einem Zinssatz von 6 % erreicht?
Wir wollen, dass die Zinsen das Dreifache des Kapitals betragen, also ist der Endbetrag gleich dem Vierfachen des Kapitals
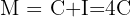
Wir stellen fest, dass wir den Endbetrag, das Kapital und den Zinssatz haben
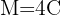
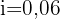
Da das Kapital ungleich 0 ist, streichen wir 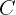in der Gleichung, um die Zeit zu berechnen
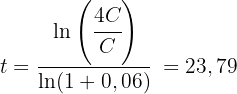
Die benötigte Zeit liegt also bei 23,79 Jahren.
Berechne den Zinseszins, der sich über fünf Jahre auf ein Kapital von 30.000 € zu 6 % ergibt.
Wir stellen fest, dass wir den Zeitraum der Investition, das Kapital und den Zinssatz haben
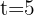
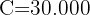
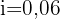
Hier müssen wir den Wert von 
ermitteln. Da wir bereits über alle erforderlichen Angaben verfügen, brauchen wir nur noch die Formel anwenden:
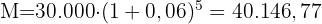
Der Zinseszins wäre also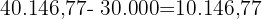 
€ nach fünf Jahren.
Berechne das Endkapital nach sechs Monaten, ausgehend von einem Anfangskapital von 10.000 € und einem Zinseszinssatz von 3,5 % pro Monat
Wir stellen fest, dass wir die Laufzeit der Investition, das Kapital und den Zinssatz haben
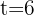
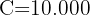
Um diese Aufgabe zu lösen, setzen wir direkt in die Formel zur Berechung des Endbetrags ein
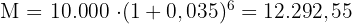
Das Kapital beträgt nach 6 Monaten 12.292,55 €.
Berechne den nominalen Zinssatz einer Investition von 30.000 €, die nach fünf Jahren mit vierteljährlicher Verzinsung zu 50.000 € wird.
Wir stellen fest, dass wir den Zeitpunkt der Investition, das Kapital und den Endbetrag haben
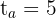
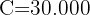
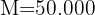
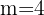
Wir berechnen die Laufzeit der Investition
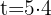
Hier müssen wir den Wert 
finden. Da wir bereits über alle erforderlichen Angaben verfügen, brauchen wir nur die Formel für die Berechnung des Wertes:
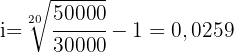
Wir setzen die Werte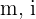 
in die Formel für den Nominalzinssatz ein und erhalten
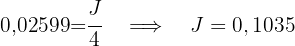
Der Nominalzinssatz beträt somit 10,35 %.
Wie lange dauert es, bis ein Kapital von 30.000 € bei einem Zinseszins von 4 % einen Betrag von 40.000 € ergibt?
Wir stellen fest, dass wir den Endbetrag, das Kapital und den Zinssatz haben
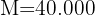
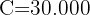
Wir setzen die Werte in die Gleichung zur Berechnung der Zeit ein
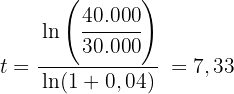
Die benötigte Zeit beträgt also 7,33 Jahre.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
