Kapitel

Definition von Brüchen
Ein Bruch ist der Quotient zweier ganzer Zahlen  und
und  und wird wie folgt dargestellt:
und wird wie folgt dargestellt:
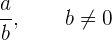
Arten von Brüchen
Echte Brüche
Es handelt sich um Brüche, deren Zähler kleiner ist als der Nenner. Ihr Wert liegt zwischen null und eins. Beispiele sind
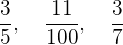
Unechte Brüche
Unechte Brüche sind solche, bei denen der Zähler größer ist als der Nenner. Ihr Wert ist größer als  . Beispiele sind
. Beispiele sind
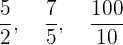
Bestimme die folgenden Brüche als echte oder unechte Brüche

 - Echt
- Echt

 - Echt
- Echt

 - Unecht
- Unecht
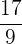
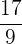 - Unecht
- Unecht

 - Unecht
- Unecht
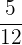
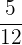 - Echt
- Echt

 - Echt
- Echt

 - Unecht
- Unecht
Gemischte Zahlen
Eine gemischte Zahl ist eine Zahl, die sich aus einer ganzen und einer gebrochenen Zahl zusammensetzt.
Um eine gemischte Zahl in einen Bruch umzuwandeln, bleibt der Nenner gleich und der Zähler ist die Summe aus dem Produkt der ganzen Zahl und dem Nenner plus dem Zähler der gemischten Zahl.
Um einen unechter Bruch in eine gemischte Zahl umzuwandeln, wird der Zähler durch den Nenner dividiert. Der Quotient ist die ganze Zahl der gemischten Zahl und der Rest ist der Zähler des Bruchs, wobei der Nenner gleich bleibt.
Wenn wir zum Beispiel die gemischte Zahl  haben, wandeln wir folgt in einen Bruch um
haben, wandeln wir folgt in einen Bruch um
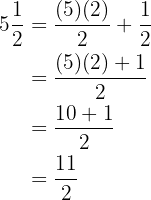
Und um den unechten Bruch  umzuwandeln gehen wir wie folgt vor:
umzuwandeln gehen wir wie folgt vor:
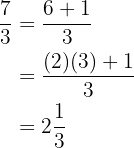
Uneigentliche Brüche und Stammbrüche
Bei uneigentlichen Brüchen ist der Zähler genauso groß wie der Nenner. Der numerische Wert ist  . Beispiele für uneigentliche Brüche sind
. Beispiele für uneigentliche Brüche sind
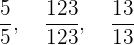
Stammbrüche haben die Einheit als Zähler. Zum Beispiel

Dezimalbrüche
Bei Dezimalbrüchen ist der Nenner eine Potenz  .
.
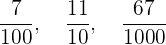
Gleiche Brüche
Zwei Brüche sind gleich, wenn Folgendes gilt

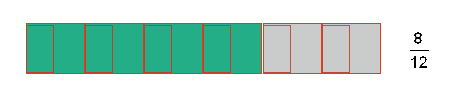
Ein Beispiel für zwei gleiche Brüche ist
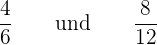
Dies ist auch in der folgenden Abbildung zu sehen

Überprüfe, ob die folgenden Brüche gleich sind oder nicht
 und
und 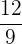
Wir überprüfen nun, ob die Brüche gleich sind oder nicht.
Wir multiplizieren den entsprechenden Zähler mit dem entsprechenden Nenner
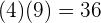
und
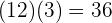
Wir erhalten folgendes Ergebnis
 ,
,
weshalb die Brüche gleich sind.
 und
und 
Wir überprüfen nun, ob die Brüche gleich sind oder nicht.
Wir multiplizieren den entsprechenden Zähler mit dem entsprechenden Nenner

und
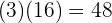
Wir erhalten folgendes Ergebnis
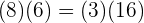 ,
,
weshalb die Brüche gleich sind.
 und
und 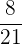
Wir überprüfen nun, ob die Brüche gleich sind oder nicht.
Wir multiplizieren den entsprechenden Zähler mit dem entsprechenden Nenner
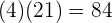
und
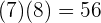
Wir erhalten folgendes Ergebnis
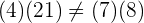 ,
,
weshalb die Brüche nicht gleich sind.
 und
und 
Wir überprüfen nun, ob die Brüche gleich sind oder nicht.
Wir multiplizieren den entsprechenden Zähler mit dem entsprechenden Nenner
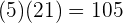
und

Wir erhalten folgendes Ergebnis
 ,
,
weshalb die Brüche gleich sind.
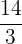 und
und 
Wir überprüfen nun, ob die Brüche gleich sind oder nicht.
Wir multiplizieren den entsprechenden Zähler mit dem entsprechenden Nenner
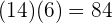
und
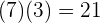
Wir erhalten folgendes Ergebnis
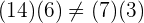 ,
,
weshalb die Brüche nicht gleich sind.
Wenn wir den Zähler und den Nenner eines Bruchs mit einer ganzen Zahl außer 0 multiplizieren oder dividieren, erhalten wir einen anderen Bruch, der dem gegebenen Bruch entspricht. Zum Beispiel
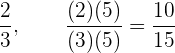
dieser letzte Bruch ist ein gleicher Bruch. Dieser Fall wird als Erweiterung bezeichnet, da wir multiplizieren.
Ein weiteres Beispiel wäre
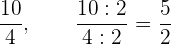
dieser letzte Bruch ist ein gleicher Bruch. Dieser Fall wird Vereinfachung genannt, da wir dividieren.
Unkürzbare Brüche
Unkürzbare Brüche sind Brüche, die nicht vereinfacht werden können. Dies ist der Fall, wenn der Zähler und der Nenner keinen gemeinsamen Faktor haben. Die folgenden Brüche sind zum Beispiel unkürzbar

Der Bruch 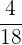 ist jedoch kürzbar
ist jedoch kürzbar
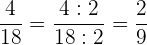
Brüche auf einen gemeinsamen Nenner bringen
Mehrer Brüche auf einen gemeinsamen Nenner zu bringen bedeutet, sie in gleichnamige Brüche mit gleichem Nenner umzuwandeln. Um dies zu tun:
1 Es wird der gemeinsame Nenner bestimmt, der das kleinste gemeinsame Vielfache der Nenner ist.
2 Dieser gemeinsame Nenner wird durch jeden der Nenner geteilt und der erhaltene Quotient mit dem entsprechenden Zähler multipliziert.
Die Brüche  und
und  zum Beispiel. Ihr gemeinsamer Nenner ist
zum Beispiel. Ihr gemeinsamer Nenner ist
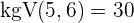
Daher können wir beide Brüche wie folgt ausdrücken
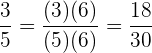
y
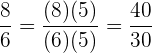
Vergleich von Brüchen
Wir können zwei Brüche anhand ihres Nenners und ihres Zählers vergleichen. Im Allgemeinen gibt es diese drei Fälle:
Brüche mit gleichem Nenner
Von zwei Brüchen mit gleichem Nenner ist derjenige mit dem kleineren Zähler kleiner.
Zum Beispiel die Brüche

Beide haben den gleichen Nenner. Da aber 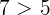 , gilt
, gilt
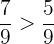
Brüche mit gleichem Zähler
Von zwei Brüchen mit gleichem Zähler ist derjenige mit dem größeren Nenner kleiner.
Zum Beispiel die Brüche

Beide haben den gleichen Zähler. Da aber 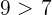 , gilt
, gilt
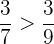
Mit unterschiedlichen Zählern und Nennern
In diesem Fall ist es nicht kompliziert. Zunächst einmal müssen wir sie auf einen gemeinsamen Nenner bringen. Sobald dies geschehen ist, können wir die Zähler direkt vergleichen, da sie nun denselben gemeinsamen Nenner haben.
Zum Beispiel die Brüche

Der gemeinsame Nenner ist 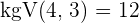 . Somit:
. Somit:

Und da 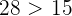 , gilt
, gilt
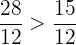
oder auch
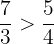
Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die als Quotient zweier ganzer Zahlen dargestellt werden kann, deren Nenner ungleich Null ist. Wir bezeichnen die Menge aller rationalen Zahlen als 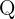 .
.
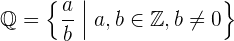
Rechnen mit rationalen Zahlen
Addition und Subtraktion von rationalen Zahlen
Bei gleichem Nenner addiert (oder subtrahiert) man einfach die Zähler und behält den Nenner bei. Zum Beispiel die Addition
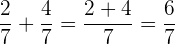
oder auch die Subtraktion
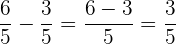
Wenn die Nenner verschieden sind, werden sie auf einen gemeinsamen Nenner gebracht und die Zähler der erhaltenen gleichen Brüche werden addiert (oder subtrahiert). Betrachten wir zum Beispiel die folgende Addition
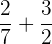
Hauptnenner 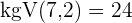 und somit
und somit
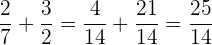
Subtraktion
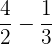
Hauptnenner: 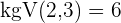 und somit
und somit
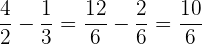
Für die Addition von rationalen Zahlen gilt Folgendes:
1 Abgeschlossenheit. Eine Rechenoperation gilt als abgeschlossen, wenn die Verknüpfung von zwei Elementen einer Menge dazu führt, dass auch die Ergebnisse zu dieser Menge gehören. Kurz gesagt: Wenn
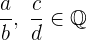 ,
,
haben wir
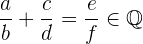
2 Assoziativ. Hierbei gilt
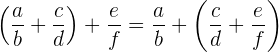
3 Kommutativ. Dieses Gesetz besagt, dass
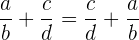
4 Neutrales Element. Hierbei ist  das neutrale Element. Es gilt:
das neutrale Element. Es gilt:
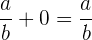
5 Invers. Dies besagt:
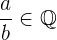
somit existiert auch
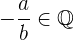
und es gilt, dass

Produkt aus rationalen Zahlen
Das Produkt von zwei rationalen Zahlen ist eine weitere rationale Zahl, deren Zähler das Produkt der Zähler und deren Nenner das Produkt der Nenner ist. Dies ist

Für das Produkt rationaler Zahlen gelten die folgenden Eigenschaften:
1 Abgeschlossenheit. Eine Rechenoperation gilt als abgeschlossen, wenn die Verknüpfung von zwei Elementen einer Menge dazu führt, dass auch die Ergebnisse zu dieser Menge gehören. Kurz gesagt: Wenn
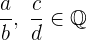 ,
,
gilt, dass
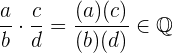
2 Assoziativ. Hierfür gilt immer, dass
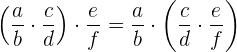
3 Kommutativ. Dieses Gesetz besagt, dass
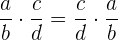
4 Neutrales Element. Hierbei ist  das neutrale Element. Es gilt:
das neutrale Element. Es gilt:

5 Invers. Dies besagt:
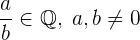
somit existiert auch

und es gilt, dass
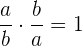
6 Distributiv:
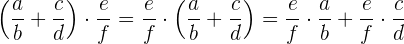
Quotient rationaler Zahlen
Für den Quotient rationaler Zahlen gilt:
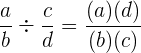
Potenzen rationaler Zahlen
Daraus folgt, dass eine rationale Zahl, die auf die n-te Potenz erhöht wird, gleich der Erhöhung von Zähler und Nenner auf die n-te Potenz ist. Kurz gesagt:

Für die Potenzen rationaler Zahlen gelten die folgenden Eigenschaften
1 
2 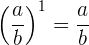
3 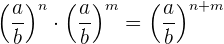
4 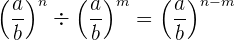
5 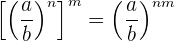
6 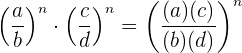
7 
Reihenfolge der Rechenoperationen
Da die rationalen Zahlen eine Teilmenge der reellen Zahlen sind, gilt auch für sie die Reihenfolge der Rechenoperationen, d. h. die Operationen werden in der folgenden Reihenfolge ausgeführt
1 Rechenoperationen innerhalb von Klammern.
2 Potenzen und Wurzeln.
3 Multiplikation und Division.
4 Addition und Subtraktion.
Mit KI zusammenfassen:












