Kapitel
Natürliche Zahlen werden verwendet, um die Elemente einer Menge zu zählen (Kardinalzahl). Oder um die Position oder Reihenfolge auszudrücken, die ein Element in einer Menge einnimmt (Ordinalzahl).
Wir erinnern uns an die Eigenschaften der natürlichen Zahlen.
Eigenschaften der Addition
Wenn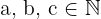 
, gelten für die Addition folgende Regeln
1 Intern: Die Summe zweier natürlicher Zahlen ergibt ebenfalls eine natürliche Zahl
2 Assoziativ:
3 Kommutativ: Die Reihenfolge der Summanden ändert das Ergebnis nicht, d. h.
4 Existenz eines neutralen Elements: Es gibt ein Element, das als neutrales Element bezeichnet wird und mit 
bezeichnet wird, so dass jede natürliche Zahl, die mit diesem Element addiert wird, die natürliche Zahl ergibt, d. h.
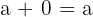
Eigenschaften der Subtraktion
1 Es handelt sich nicht um eine interne Operation: Die Subtraktion zweier natürlicher Zahlen ergibt nicht unbedingt eine natürliche Zahl, z. B.
2 Nicht kommutativ: Die Reihenfolge der Subtraktion ändert das Ergebnis, z. B.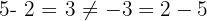
Eigenschaften der Multiplikation
1 Intern: Die Multiplikation zweier natürlicher Zahlen ergibt eine natürliche Zahl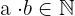 
2 Assoziativ: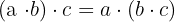
3 Kommtutativ: Die Reihenfolge der Multiplikation ändert das Ergebnis nicht,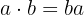 
4 Neutrales Element: Es gibt ein Element, das als neutrales Element bezeichnet wird und mit 
gekennzeichnet ist, so dass jede natürliche Zahl, die mit diesem Element multipliziert wird, die gleiche natürliche Zahl ergibt, 
5 Distribution in Bezug auf die Addition: 
6 Gemeinsamen Faktor ausklammern:
Eigenschaften der Addition
1 Exakte Division: Eine Division ohne Rest ist eine Division, bei der der Rest 0 ist. Das heißt, 
, wobei 
der Dividend, 
der Divisor und 
der Quotient ist.
2 Division mit Rest: Bei einer Division mit Rest bleibt ein Rest, der ungleich 0 ist,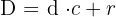 
, wobei 
den Rest darstellt.
3 Nicht intern: Die Division zweier natürlicher Zahlen, ergibt nicht unbedingt eine natürliche Zahl, z. B.
4 No es Conmutativo: al dividir, sí importa el orden, no es lo mismo 
que 
, por ejemplo
5 Null geteilt durch eine beliebige Zahl ergibt null: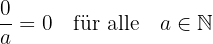
6 Es kann nicht durch 0 dividiert werden.
Eigenschaften von Potenzen
Gegeben ist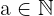 
:
1 Jede natürliche Zahl hoch 0 ist 1 
22 Jede natürliche Zahl zur Potenz 1, ergibt dieselbe natürliche Zahl
3 Produkt von Potenzen mit gleicher Basis:
4 Quotient von Potenzen mit gleicher Basis: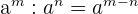
5 Potenz einer Potenz:
6 Produkt aus Potenzen mit gleichem Exponenten: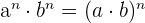
7 Quotient von Potenzen mit gleichem Exponenten: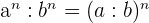
Eigenschaften von Wurzeln
1 Quadratwurzel: Die Quadratwurzel hat den Rest , das heißt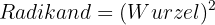
Zum Beispiel:
2 Ungerade Wurzel: Bei einer ungeraden Wurzel bleibt immer ein Rest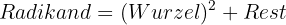
Zum Beispiel:
Reihenfolge der Rechenoperationen
Bei Rechenoperationen mit natürlichen Zahlen muss folgende Reihenfolge eingehalten werden:
1. Rechenoperationen, die in Klammern stehen.
2. Potenzen und Wurzeln.
3. Multiplikation und Division.
4. Addition und Subtraktion.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
