Kapitel

Definition einer arithmetischen Folgen
Eine arithmetische Folge ist eine Folge von Zahlen, bei der jede Zahl (mit Ausnahme der ersten) gleich der vorhergehenden plus einer festen Zahl, der Differenz, ist, die mit  angegeben wird.
angegeben wird.
Somit 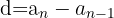
Beispiel:
Arithmetische Folge 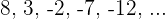
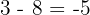



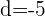
Es handelt sich um eine arithmetische Folge, die durch Addition von  zum vorherigen Term gebildet wird. Die darauffolgenden Terme wären also:
zum vorherigen Term gebildet wird. Die darauffolgenden Terme wären also:

Wir stellen fest, dass der Ausdruck 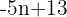 den n-ten Term der Folge ergibt.
den n-ten Term der Folge ergibt.
Um zum Beispiel den vierten Term der Folge zu erhalten, substituieren wir mit  ,
,
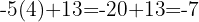
Dieser Ausdruck ist das allgemeine Glied.
Das allgemeine Glied berechnen
Um das allgemeine Glied in einer arithmetischen Folge zu berechnen, betrachten wir die beiden folgenden Fälle:
1 Wenn das 1. Glied bekannt ist.
Das allgemeine Glied ist durch folgende Formel gegeben: 
Beispiel:
Arithmetische Folge 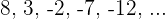
1. Glied 
Allgemeines Glied 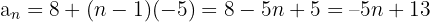
2 Wenn wir den Wert kennen, den ein beliebiger anderes Glied der Folge einnimmt.
Das allgemeine Glied ist durch folgende Formel gegeben: 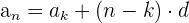
Beispiel:
Arithmetische Folge 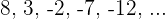
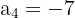
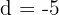
Allgemeines Glied 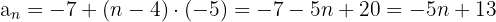
Interpolation von Gliedern einer arithmetischen Folge
Bei der Interpolation von Mittelwerten zwischen zwei Zahlen handelt es sich um die Konstruktion einer arithmetischen Folge mit den gegebenen Zahlen als Extremwerten.
Gegeben sind die Extremwerte  und
und  sowie die Anzahl der zu interpolierenden Mittelwerte
sowie die Anzahl der zu interpolierenden Mittelwerte  . Die Differenz ist gegeben durch:
. Die Differenz ist gegeben durch:
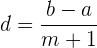
Beispiel:
Interpoliere drei arithmetische Mittel zwischen  und
und  .
.
Wir haben die Werte
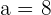

Unter Verwendung der Formel
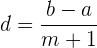
erhalten wir den Wert von 
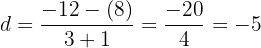
Schließlich
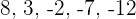
Summe äquidistanter Glieder einer arithmetischen Folge
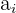 und
und 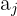 sind zwei Glieder, die von den Extremwerten gleich weit entfernt sind. Es gilt, dass die Summe gleich weit entfernter Glieder gleich der Summe der Extremwerte ist.
sind zwei Glieder, die von den Extremwerten gleich weit entfernt sind. Es gilt, dass die Summe gleich weit entfernter Glieder gleich der Summe der Extremwerte ist.
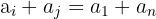
Somit gilt, dass
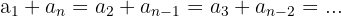
Beispiel:
Arithmetische Folge 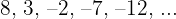

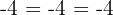
Summe aus n aufeinanderfolgenden Gliedern einer arithmetischen Folge
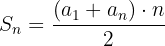
Beispiel:
Berechne die Summe der ersten  Glieder der Folge:
Glieder der Folge: 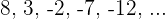
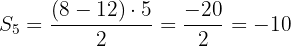
Mit KI zusammenfassen:












