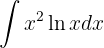
Dieses Integral lösen wir mit der Methode der partiellen Integration, das heißt  .
.
Also wählen wir 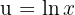 und
und 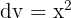 . Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten:
. Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten: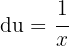
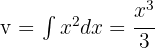 .
.
Wir verwenden die Formel der partiellen Integration und erhalten: 
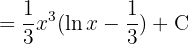
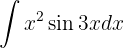
Dieses Integral lösen wir mit der Methode der partiellen Integration, das heißt .
.
Also wählen wir 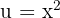 und
und 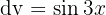 . Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten:
. Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten: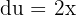
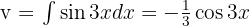 .
.
Wir verwenden die Formel der partiellen Integration und erhalten: 
Wir stellen fest, dass wir die Methode der partiellen Integration erneut anwenden müssen und nehmen  und
und 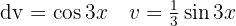
Wir kehren zur Aufgabe zurück und setzen die Werte ein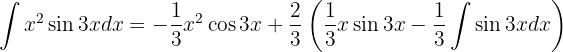

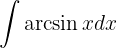
Dieses Integral lösen wir mit der Methode der partiellen Integration, das heißt .
.
Also wählen wir 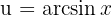 y
y 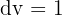 . Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten:
. Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten: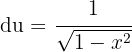
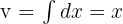 .
.
Wir verwenden die Formel der partiellen Integration und erhalten: 
Für das Integral substituieren wir 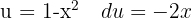 und wandeln so um
und wandeln so um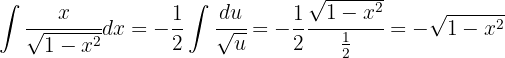
Wenn wir schließlich den Wert dieses Integrals einsetzen, können wir die Aufgabe lösen: 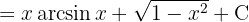
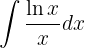
Dieses Integral lösen wir mit der Methode der partiellen Integration, das heißt .
.
Also wählen wir 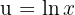 und
und  . Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten:
. Das Erste leiten wir ab und das Zweite integrieren wir. Wir erhalten: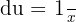
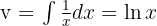 .
.
Wir verwenden die Formel der partiellen Integration und erhalten: 
Wir stellen fest, dass es sich um ein sich wiederholendes Integral handelt, d.h. wir sind zum ursprünglichen Integral zurückgekehrt. Somit ist 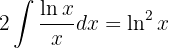 Schließlich ermitteln wir das Integral.
Schließlich ermitteln wir das Integral. 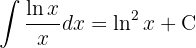
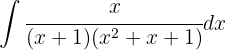
Dieses Integral lösen wir mit der Methode der partiellen Integration. Wir beginnen und trennen den Bruch wie folgt: 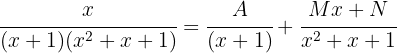
Wir addieren auf der rechten Seite und erhalten: 
Wir eliminieren gleiche Nennen und fassen zusammen: 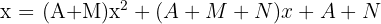 Wir stellen das folgende Gleichungssystem auf.
Wir stellen das folgende Gleichungssystem auf.
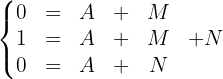
Aus der 1. und letzten Gleichung erhalten wir 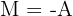 y
y 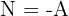
Wir setzen in die zweite Gleichung ein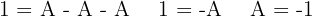
Somit ist  und
und 
Das erste Integral kann wie folgt aufgeteilt werden:
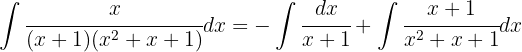
Das erste Integral ist logarithmisch und das zweite Integral muss in zwei Integrale zerlegt werden, die logarithmisch und vom Typ Arkustangens sind.
Wir beginnen damit, das zweite Integral mit 2 zu multiplizieren und dann so zu trennen, dass wir die beiden oben genannten Arten von Integralen erhalten.
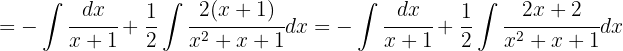
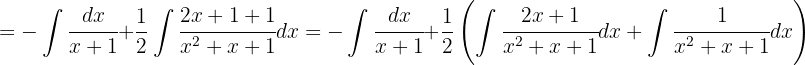
Schließlich können wir die Integrale vom Typ Logarithmus und für das letzte Integral vom Typ Arkustangens anwenden.
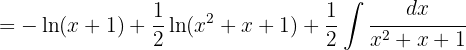
Wir wandeln den Nenner so um, dass wir die Formel für das Integral des Arkustangens anwenden können.
TWir wandeln den Nenner in ein Binom zum Quadrat um.
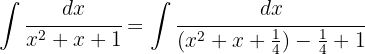

Wir multiplizieren Zähler und Nenner mit 4/3, um im Nenner 1 zu erhalten.
Innerhalb des Binoms zum Quadrat multiplizieren wir mit der Quadratwurzel aus 4/3.
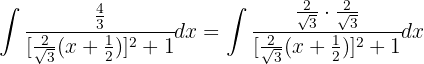
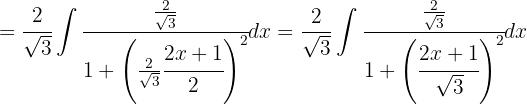
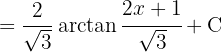
Fügt man schließlich alle Teile zusammen, so lautet das ursprüngliche Integral:

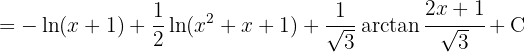
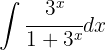
Bei diesem Integral führen wir eine Substitution durch: 
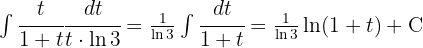
Wir kehren zur ursprünglichen Variablen zurück und erhalten das Ergebnis. 

Wir beginnen mit folgender Substitution: 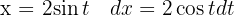
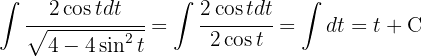
Nach der Substitution bestimmen wir t, um zu unserer ursprünglichen Variablen zurückzukehren: 
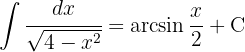
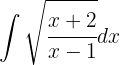
Wir beginnen mit folgender Substitution: 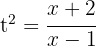 , bestimmen den Wert von x,
, bestimmen den Wert von x,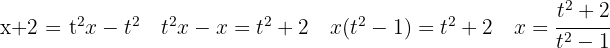

Wir wenden die partielle Integration an .
. 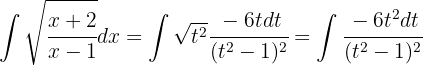
Also wählen wir 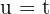 und
und 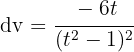 . Wir leiten das Erste ab und integrieren das Zweite:
. Wir leiten das Erste ab und integrieren das Zweite: 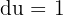
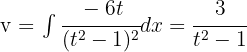 . Wir wenden die partielle Integration an und erhalten:
. Wir wenden die partielle Integration an und erhalten: 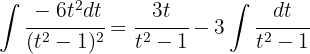
Das letzte Integral lösen wir als partielles Integral:
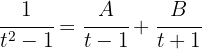
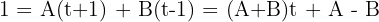
Wir erhalten das folgende System: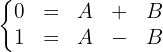
Aus der 1. Gleichung erhalten wir 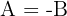 . Wir setzen in die 2. Gleichung ein:
. Wir setzen in die 2. Gleichung ein: , somit ist
, somit ist 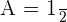
Wir kehren zum Integral zurück und erhalten: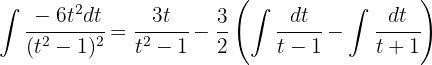
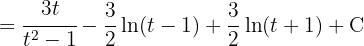
Wir kehren zur ursprünglichen Variablen zurück 
Wir setzen ein und erhalten
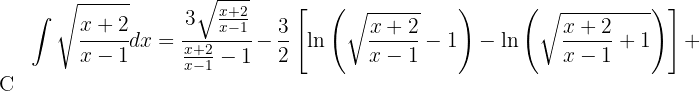
Wir wenden die Regeln für den Logarithmus an.
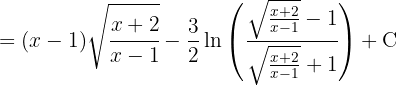
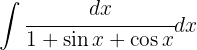
Wir beginnen mit folgender Substitution: 
Wir setzen ein und erhalten
Wir vereinfachen und kehren zur ursprünglichen Variablen zurück: 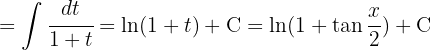
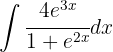
Wir substituieren: 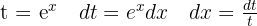 ,
,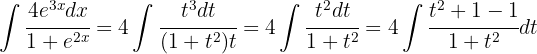
Wir vereinfachen und kehren zur ursprünglichen Variablen zurück: 
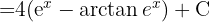
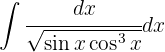
Wir beginnen mit folgender Substitution:  ,
,
Wir vereinfachen schließlich und kehren zur ursprünglichen Variablen zurück: 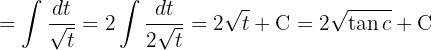
Mit KI zusammenfassen:


