Willkommen auf unserer Seite, die sich mit Übungen und Anwendungen der Binomialverteilung beschäftigt. Die Binomialverteilung ist ein grundlegendes Instrument in der Wahrscheinlichkeitstheorie und wird verwendet, um Ereignisse zu beschreiben, die zwei mögliche Ergebnisse haben können, z. B. Erfolg oder Misserfolg, ja oder nein. In diesem Leitfaden führen wir dich durch eine Reihe von Übungen und Anwendungen, die diese Verteilung und ihre Bedeutung in verschiedenen Kontexten untersuchen.
Die Binomialverteilung ist gekennzeichnet durch die Erfolgswahrscheinlichkeit in jedem Versuch, die Gesamtzahl der Versuche und das Interesse daran, zu zählen, wie viele Erfolge in einer Reihe von unabhängigen Versuchen auftreten. Im Laufe dieses Leitfadens lernen wir, wie man die Binomialverteilung anwendet, um Wahrscheinlichkeiten von Ereignissen zu berechnen, wie z. B. die Anzahl der Erfolge in einer bestimmten Anzahl von Versuchen oder die Wahrscheinlichkeit, dass ein bestimmtes Ereignis in einer bestimmten Anzahl von Wiederholungen auftritt.
Eine Münze wird viermal geworfen. Berechne die Wahrscheinlichkeit, dass es mehr Kopf als Zahl geworfen wird.
Beim Werfen einer Münze liegt die Wahrscheinlichkeit, dass Kopf geworfen wird, bei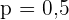 
und dass Zahl geworfen wird, bei 
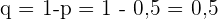. In diesem Fall wird das Wurfexperiment viermal durchgeführt und somit ist 
. Daher haben wir die Binomialverteilung 
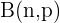mit folgenden Parametern:
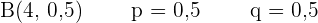
Da wir nun wissen wollen, wie hoch die Wahrscheinlichkeit ist, dass mehr Kopf als Zahl geworfen wird, sind die Ereignisse, bei denen dies der Fall ist, entweder dreimal Kopf und einmal Zahl oder viermal Kopf und keine Zahl, so dass,
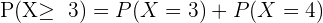
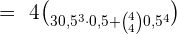
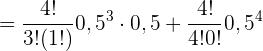
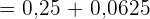
Ein Versicherungsvertreter verkauft Versicherungspolicen an 5 Personen im gleichen Alter und bei guter Gesundheit. Nach den aktuellen Statistiken beträgt die Wahrscheinlichkeit, dass eine Person in diesem Zustand 
Jahre oder länger leben wird, 
. Berechne die Wahrscheinlichkeit, dass sie nach noch leben:
a Alle 5 Personen.
b Mindestens 3 Personen.
c Genau 2 Personen.
Betrachten wir die Binomialverteilung 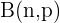mit den folgenden Parametern:
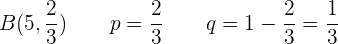
a Alle 5 Personen.
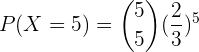
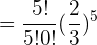
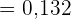
b Mindestens 3 Personen.
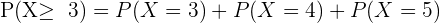
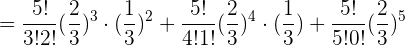
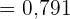
c Genau 2 Personen.
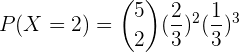
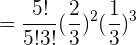
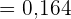
Wenn von 6 bis 7 Uhr abends jede fünfte Telefonnummer besetzt ist, wie groß ist dann die Wahrscheinlichkeit, dass bei der Wahl von 
zufällig ausgewählten Telefonnummern nur zwei besetzt sind?
Betrachten wir die Binomialverteilung 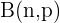mit den folgenden Parametern:
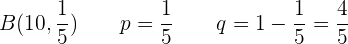
Wir berechnen die Wahrscheinlichkeit, dass bei der Wahl von Telefonnummern nur zwei besetzt sind.
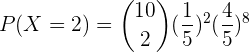
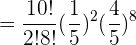
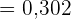
Die Wahrscheinlichkeit, dass ein Mann das Ziel trifft, ist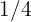 
. Wenn er Mal schießt.
a Wie hoch ist die Wahrscheinlichkeit, dass er genau dreimal trifft?
b Wie hoch ist die Wahrscheinlichkeit, dass er mindestens einmal trifft?
Betrachten wir die Binomialverteilung 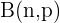mit den folgenden Parametern:
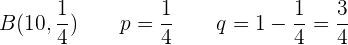
a Wie hoch ist die Wahrscheinlichkeit, dass er genau dreimal trifft?
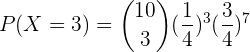
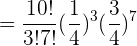
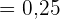
b Wie hoch ist die Wahrscheinlichkeit, dass er mindestens einmal trifft?
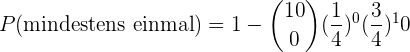
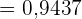
In einer Urne befinden sich Kugeln, rote und der Rest sind weiße Kugeln. Eine Kugel wird nach dem Zufallsprinzip gezogen und es wird notiert, ob sie rot ist; der Vorgang wird unter Zurücklegen der Kugel Mal wiederholt. Berechne den Mittelwert und die Standardabweichung
Betrachten wir die Binomialverteilung 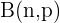mit den folgenden Parametern:
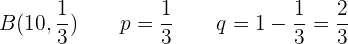
Mittelwert:
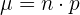
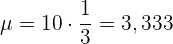
Standardabweichung:
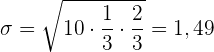
Bei Alkoholtests wurde festgestellt, dass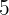 
der kontrollierten Fahrer positiv waren und dass 
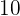der kontrollierten Fahrer den Sicherheitsgurt nicht angelegt hatten. Es wurde auch festgestellt, dass die beiden Verstöße unabhängig voneinander auftreten.
a Berechne die Wahrscheinlichkeit, dass genau 3 Fahrer einen der beiden Verstöße begangen haben.
b Berechne die Wahrscheinlichkeit, dass mindestens einer der kontrollierten Fahrer einen der beiden Verstöße begangen hat.
Wir definieren die folgenden Ereignisse:
A: Fahrer testen positiv auf Alkohol.
B: Fahrer sind nicht angeschnallt.
Die Wahrscheinlichkeit, dass der Fahrer positiv getestet wird oder den Sicherheitsgurt nicht anlegt oder dass beide Ereignisse eintreten, wenn man weiß, dass die Verstöße unabhängig voneinander sind, beträgt dann: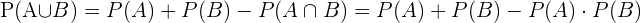
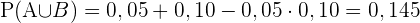
Nun betrachten wir die Binomialverteilung B(n,p) mit den folgenden Parametern:
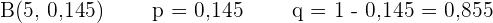
a Berechne die Wahrscheinlichkeit, dass genau drei Fahrer einen der beiden Verstöße begangen haben.
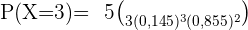
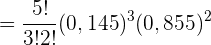
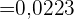
b Berechne die Wahrscheinlichkeit, dass mindestens einer der kontrollierten Fahrer einen der beiden Verstöße begangen hat.
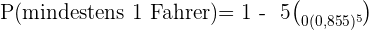
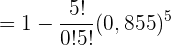
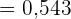
Ein Labor gibt an, dass ein Medikament bei 
von 
Patienten Nebenwirkungen verursacht. Um diese Behauptung zu überprüfen, wählt ein anderes Labor zufällig 
Patienten aus, denen das Medikament verabreicht wird. Wie hoch ist die Wahrscheinlichkeit der folgenden Ereignisse?
a Bei keinem Patienten treten Nebenwirkungen auf.
b Bei mindestens 2 Patienten treten Nebenwirkungen auf.
c Wie hoch ist die durchschnittliche Zahl der Patienten, bei denen das Labor Nebenwirkungen erwartet, wenn Patienten zufällig ausgewählt werden?
Betrachten wir die Binomialverteilung 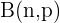mit den folgenden Parametern:
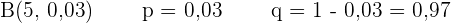
a Bei keinem Patienten treten Nebenwirkungen auf.
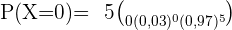
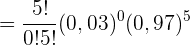
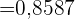
b Bei mindestens 2 Patienten treten Nebenwirkungen auf.
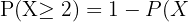
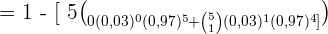
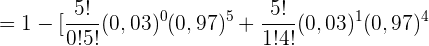
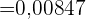
c Wie hoch ist die durchschnittliche Zahl der Patienten, bei denen das Labor Nebenwirkungen erwartet, wenn 100 Patienten zufällig ausgewählt werden?
Media:
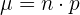
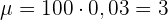
Eine Baseballmannschaft mit einem Schlagdurchschnitt von 0,300 (30 % Erfolgsquote) führt 10 unabhängige Versuche durch. Wie groß ist die Wahrscheinlichkeit, dass sie bei jedem dieser Versuche mindestens 5 Runs erzielt?
Die Wahrscheinlichkeit des mindestens 5-maligen Auftretens ist gegeben durch
Wir berechnen daher jede dieser Wahrscheinlichkeiten mithilfe der Binomialverteilung mit 
und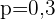 
.
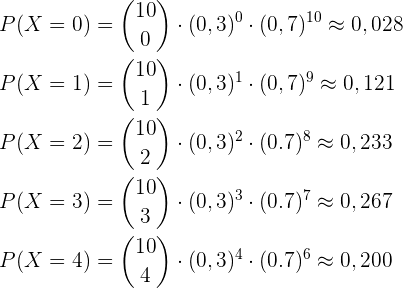
Das heißt: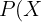 
Angenommen, du hast eine Münze und möchtest berechnen, wie viele Würfe du brauchst, damit die Wahrscheinlichkeit, mindestens 3 Mal Kopf zu erhalten, gleich oder größer als 90 % ist. Du weißt, dass die Wahrscheinlichkeit, bei einem einzigen Wurf Kopf zu erhalten, 50 % (0,5) beträgt.
a Wie viele Münzwürfe sind nötig, um mit einer Wahrscheinlichkeit von mindestens 90 % mindestens 3 Mal Kopf zu erhalten?
b Wie hoch ist die Wahrscheinlichkeit, bei dieser Anzahl von Würfen mindestens 3 Mal Kopf zu werfen?
a
Wir möchten eine Zahl 
finden, mit der wir 
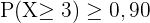erhalten. Um eine solche Zahl zu erhalten, müssen wir die Wahrscheinlichkeit für jedes dieser Ereignisse mit mindestens 3 Würfen berechnen, bis wir eines finden, das die Bedingung erfüllt. Zunächst können wir die Verteilungsfunktion mit dem gesuchten schreiben:
Ersetzt man (die Anzahl der Versuche) durch ganzzahlige Werte größer als 3 und berechnet das Ergebnis, so erhält man die folgenden Werte:
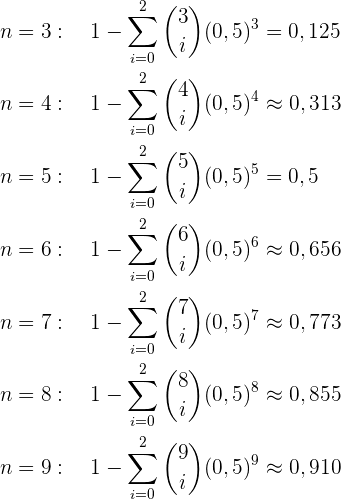
Wir brauchen also mindestens 9 Versuche, damit 3 Mal Kopf geworfen wird.
b
Berechnet man auf die gleiche Weise wie oben, so ergibt sich für die Wahrscheinlichkeit, 3 Mal Kopf bei 9 Versuchen zu erhalten, eine Wahrscheinlichkeit von
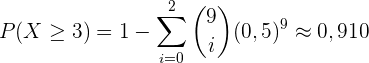
Bei einem Multiple-Choice-Test hat jede Frage 5 Antwortmöglichkeiten, von denen nur eine richtig ist. Ein Schüler entscheidet sich, alle Fragen des Tests, der aus 20 Fragen besteht, zufällig zu beantworten.
a Wie hoch ist die Wahrscheinlichkeit, dass der Schüler genau 9 Fragen richtig beantwortet?
b Berechne den Mittelwert und die Varianz.
a
Bei 5 Auswahlmöglichkeiten pro Frage ist die Wahrscheinlichkeit, eine richtige Antwort zu geben, 0,2, wenn wir zufällig wählen. Die Wahrscheinlichkeit, genau 9 richtige Antworten zu erhalten, ist also gegeben durch
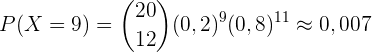
b
Beachte, dass der Mittelwert gegeben ist durch
,
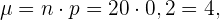wobei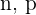 
die Anzahl der Versuche bzw. die Wahrscheinlichkeit des Ereignisses sind. Die Varianz ist gegeben durch
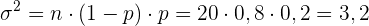
Das heißt, dass ein Schüler, der 20 Fragen nach dem Zufallsprinzip beantwortet, im Durchschnitt 4 richtige Antworten erzielt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
