Bei einem Zufallsexperiment wird ein Würfel geworfen, bei dem die erreichten Punktzahlen notiert werden sollen. Berechne:
a Die Funktion der Verteilung und ihre Darstellung
b Die Funktion der Verteilung und ihre Darstellung
c Den Erwartungswert, die Varianz und die Standardabweichung
Bei einem Zufallsexperiment wird ein Würfel geworfen, bei dem die erreichten Punktzahlen notiert werden sollen. Berechne:
a Die Funktion der Wahrscheinlichkeit und ihre Darstellung
 | 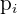 |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
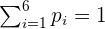 | |
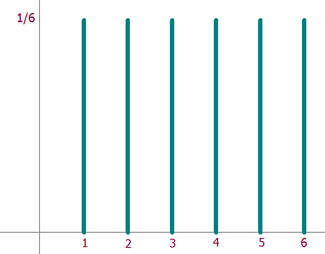
b Die Funktion der Verteilung und ihre Darstellung
 | 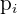 |
|---|---|
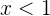 |  |
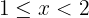 |  |
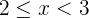 |  |
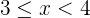 |  |
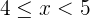 |  |
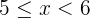 |  |
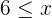 |  |
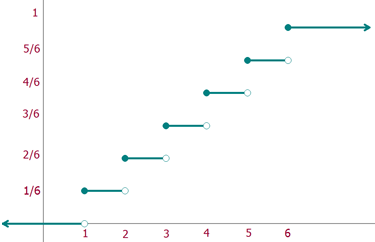
c Den Erwartungswert, die Varianz und die Standardabweichung
 | 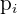 |  | 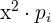 |
|---|---|---|---|
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  | 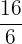 |
 |  |  | 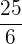 |
 |  |  |  |
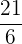 | 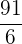 |
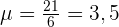
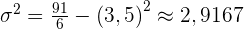
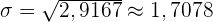
Gegeben ist eine diskrete Zufallsvariable  , deren Wahrscheinlichkeitsfunktion wie folgt ist:
, deren Wahrscheinlichkeitsfunktion wie folgt ist:
 | 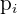 |
|---|---|
 |  |
 | 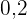 |
 |  |
 |  |
 |  |
 |  |
a Berechne die Verteilungsfunktion und stelle sie grafisch dar.
b Berechne die folgenden Wahrscheinlichkeiten:
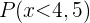
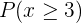
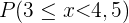
Gegeben ist eine diskrete Zufallsvariable  , deren Wahrscheinlichkeitsfunktion wie folgt ist:
, deren Wahrscheinlichkeitsfunktion wie folgt ist:
 | 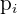 |
|---|---|
 |  |
 | 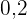 |
 |  |
 |  |
 |  |
 |  |
1 Berechne die Verteilungsfunktion und stelle sie grafisch dar
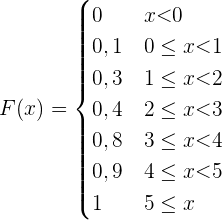
2 Berechne die folgenden Wahrscheinlichkeiten:
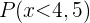
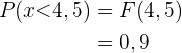
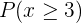
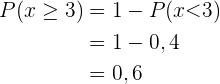
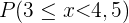
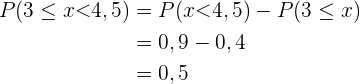
Gegeben ist die folgende Funktion der Verteilung
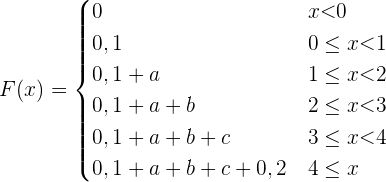 ,
,
wobei 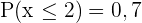 und
und 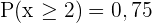 . Berechne den Erwartungswert, die Varianz und die Standardabweichung.
. Berechne den Erwartungswert, die Varianz und die Standardabweichung.
Gegeben ist die folgende Funktion der Verteilung
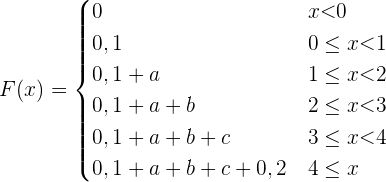 ,
,
wobei 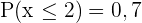 und
und 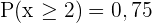 . Berechne den Erwartungswert, die Varianz und die Standardabweichung.
. Berechne den Erwartungswert, die Varianz und die Standardabweichung.
Da 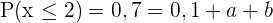 und
und 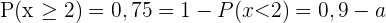 , haben wir das folgende Gleichungssystem
, haben wir das folgende Gleichungssystem
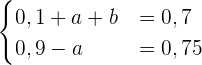
Die Lösung ist 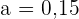 und
und 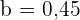 .Schließlich ergibt sich für die Verteilungsfunktion, dass
.Schließlich ergibt sich für die Verteilungsfunktion, dass
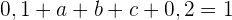
Wir setzen die Werte von 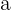 und
und 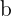 ein und lösen nach
ein und lösen nach  auf. Wir erhalten
auf. Wir erhalten 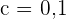 . Daraus folgt:
. Daraus folgt:
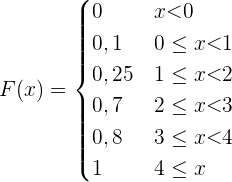
Aus der obigen Verteilungsfunktion lässt sich die Wahrscheinlichkeitsfunktion ableiten, die wie folgt gegeben ist
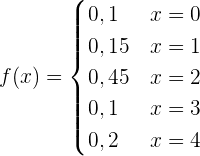
 | 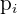 | 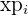 |  |
|---|---|---|---|
 |  |  |  |
 | 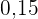 | 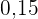 | 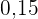 |
 | 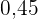 |  | 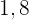 |
 |  | 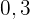 |  |
 | 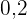 | 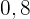 | 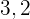 |
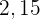 | 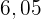 |

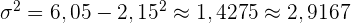
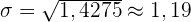
Ein Spieler wirft zwei Münzen. Er gewinnt  oder
oder  €, wenn einmal oder zweimal Kopf erscheint. Andererseits verliert er
€, wenn einmal oder zweimal Kopf erscheint. Andererseits verliert er  €, wenn Kopf nicht erscheint. Ermittle den Erwartungswert und ob dieser günstig ist.
€, wenn Kopf nicht erscheint. Ermittle den Erwartungswert und ob dieser günstig ist.
Ein Spieler wirft zwei Münzen. Er gewinnt  oder
oder  €, wenn einmal oder zweimal Kopf erscheint. Andererseits verliert er
€, wenn einmal oder zweimal Kopf erscheint. Andererseits verliert er  €, wenn Kopf nicht erscheint. Ermittle den Erwartungswert und ob dieser günstig ist.
€, wenn Kopf nicht erscheint. Ermittle den Erwartungswert und ob dieser günstig ist.
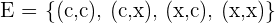



Der Erwartungswert ist durch 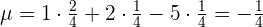 gegeben. Er ist somit nicht günstig.
gegeben. Er ist somit nicht günstig.
Es wird ein Paar Würfel geworfen. Bestimme die Zufallsvariable 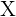 als die Summe der erhaltenen Punktzahlen. Ermittle die Wahrscheinlichkeitsfunktion, den Erwartungswert und die Varianz
als die Summe der erhaltenen Punktzahlen. Ermittle die Wahrscheinlichkeitsfunktion, den Erwartungswert und die Varianz
Es wird ein Paar Würfel geworfen. Bestimme die Zufallsvariable 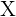 als die Summe der erhaltenen Punktzahlen. Ermittle die Wahrscheinlichkeitsfunktion, den Erwartungswert und die Varianz
als die Summe der erhaltenen Punktzahlen. Ermittle die Wahrscheinlichkeitsfunktion, den Erwartungswert und die Varianz
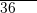
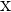 | 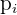 | 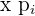 | 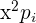 |
|---|---|---|---|
 | 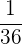 | 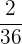 | 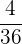 |
 | 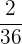 | 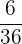 | 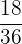 |
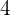 | 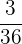 | 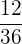 | 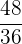 |
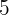 | 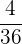 | 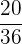 | 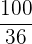 |
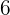 | 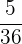 | 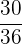 | 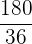 |
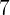 | 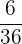 | 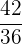 | 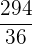 |
 | 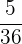 | 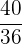 | 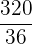 |
 | 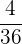 | 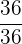 | 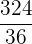 |
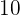 | 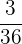 | 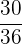 | 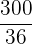 |
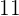 | 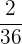 | 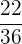 | 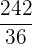 |
 | 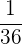 | 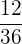 | 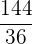 |
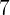 | 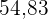 |
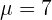
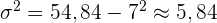
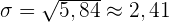
Ein Spieler würfelt mit einem gewöhnlichen Würfel. Wenn  oder eine Primzahl gewürfelt wird, gewinnt er so viele Hundert Euro, wie der Würfel Punkte zeigt. Wenn aber keine Primzahl gewürfelt wird, verliert er so viele Hundert Euro, wie der Würfel Punkte zeigt. Ermittle die Wahrscheinlichkeitsfunktion und den Erwartungswert des Spiels.
oder eine Primzahl gewürfelt wird, gewinnt er so viele Hundert Euro, wie der Würfel Punkte zeigt. Wenn aber keine Primzahl gewürfelt wird, verliert er so viele Hundert Euro, wie der Würfel Punkte zeigt. Ermittle die Wahrscheinlichkeitsfunktion und den Erwartungswert des Spiels.
Ein Spieler würfelt mit einem gewöhnlichen Würfel. Wenn  oder eine Primzahl gewürfelt wird, gewinnt er so viele Hundert Euro, wie der Würfel Punkte zeigt. Wenn aber keine Primzahl gewürfelt wird, verliert er so viele Hundert Euro, wie der Würfel Punkte zeigt. Ermittle die Wahrscheinlichkeitsfunktion und den Erwartungswert des Spiels.
oder eine Primzahl gewürfelt wird, gewinnt er so viele Hundert Euro, wie der Würfel Punkte zeigt. Wenn aber keine Primzahl gewürfelt wird, verliert er so viele Hundert Euro, wie der Würfel Punkte zeigt. Ermittle die Wahrscheinlichkeitsfunktion und den Erwartungswert des Spiels.
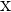 | 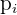 | 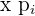 |
|---|---|---|
 |  | 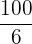 |
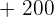 |  | 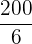 |
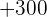 |  | 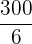 |
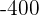 |  | 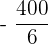 |
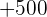 |  | 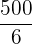 |
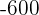 |  | 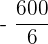 |
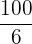 |
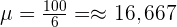
Wenn eine Person ein Lotterielos kauft, bei dem sie entweder 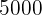 € oder einen zweiten Preis von
€ oder einen zweiten Preis von 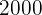 € gewinnen kann, mit Wahrscheinlichkeiten von:
€ gewinnen kann, mit Wahrscheinlichkeiten von: 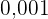 und
und 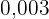 . Was wäre ein angemessener Preis für das Los?
. Was wäre ein angemessener Preis für das Los?
Wenn eine Person ein Lotterielos kauft, bei dem sie entweder 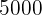 € oder einen zweiten Preis von
€ oder einen zweiten Preis von 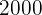 € gewinnen kann, mit Wahrscheinlichkeiten von:
€ gewinnen kann, mit Wahrscheinlichkeiten von: 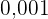 und
und 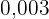 . Was wäre ein angemessener Preis für das Los?
. Was wäre ein angemessener Preis für das Los?
Der Preis ist durch den Erwartungswert gegeben
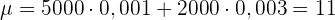 €
€
Mit KI zusammenfassen:


