Zwei Wurzeln sind äquivalent, wenn ihre gebrochenen Exponenten es ebenfalls sind.
Beispiel: 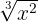 und
und 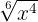 sind äquivalente Wurzeln. radicales equivalentes. Um dies zu beweisen, schreiben wir die beiden Wurzeln mit gebrochenen Exponenten
sind äquivalente Wurzeln. radicales equivalentes. Um dies zu beweisen, schreiben wir die beiden Wurzeln mit gebrochenen Exponenten
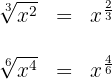
Die gebrochenen Exponenten  und
und  sind äquivalent, da das Produkt ihrer Extremwerte gleich dem Produkt ihrer Mittelwerte ist
sind äquivalent, da das Produkt ihrer Extremwerte gleich dem Produkt ihrer Mittelwerte ist

Bildung von äquivalenten Wurzeln
Um äquivalente Wurzeln zu bilden, reicht es aus, äquivalente gebrochene Exponenten zu bilden, die auf zwei Arten erhalten werden können: durch Erweiterung und Vereinfachung.
Erweiterung von Wurzeln
Dies erhält man, indem man den Zähler und den Nenner des gebrochenen Exponeten mit einer gleichen Zahl ungleich 0 multipliziert
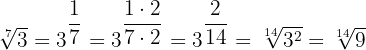
Vereinfachung von Wurzeln
Dies erhält man, indem man den Zähler und den Nenner des gebrochenen Exponenten durch eine gleiche Zahl ungleich 0 dividiert
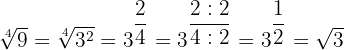
Zur Erweiterung und Vereinfachung einer Wurzel ist es nicht notwendig, sie als Bruch auszudrücken; es genügt, den Exponenten des Radikanden und den Wurzelexponenten mit der gleichen Zahl zu multiplizieren oder zu dividieren.
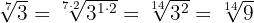
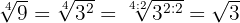
Wenn der Bruch der Potenz nicht weiter kürzbar ist, ist auch die Wurzeln nicht kürzbar.
Aufgaben mit Lösungen
Untersuche, ob die folgenden Wurzeln äquivalent sind
1 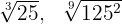
2 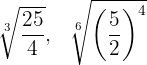
3 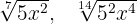
4 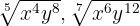
5 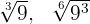
1
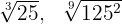
Zunächst drücken wir die beiden Wurzeln in Bruchschreibweise aus-
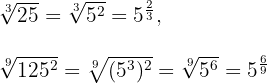
Wir untersuchen, ob die gebrochenen Exponenten 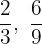 äquivalent sind
äquivalent sind 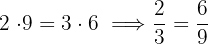 sind äquivalent und somit sind auch die Wurzeln äquivalent.
sind äquivalent und somit sind auch die Wurzeln äquivalent.
2
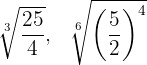
Wir drücken beide Wurzeln in Bruchschreibweise aus 
Wir untersuchen, ob die gebrochenen Exponenten 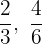 äquivalent sind
äquivalent sind 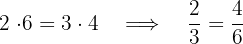 sind äquivalent und somit sind auch die Wurzeln äquivalent.
sind äquivalent und somit sind auch die Wurzeln äquivalent.
3
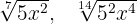
Wir drücken beide Wurzeln in Bruchschreibweise aus 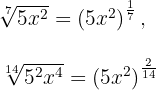
Wir untersuchen, ob die gebrochenen Exponenten 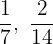 äquivalent sind
äquivalent sind 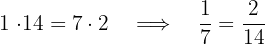 sind äquivalent und somit sind auch die Wurzeln äquivalent.
sind äquivalent und somit sind auch die Wurzeln äquivalent.
4
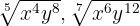
Wir untersuchen, ob die gebrochenen Exponenten 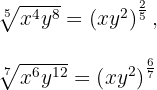
Wir untersuchen, ob die gebrochenen Exponenten 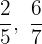 äquivalent sind
äquivalent sind 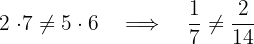 sind nicht äquivalent und somit sind auch die Wurzeln nicht äquivalent.
sind nicht äquivalent und somit sind auch die Wurzeln nicht äquivalent.
5
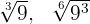
Wir drücken beide Wurzeln in Bruchschreibweise aus 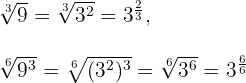
Wir untersuchen, ob die gebrochenen Exponenten 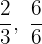 äquivalent sind
äquivalent sind 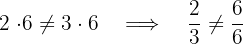 sind nicht äquivalent und somit sind auch die Wurzeln nicht äquivalent.
sind nicht äquivalent und somit sind auch die Wurzeln nicht äquivalent.
Ermittle mithilfe der Erweiterung äquivalente Wurzeln für die folgenden Wurzeln.
1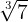
2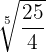
3 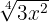
1 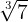
Wir multiplizieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel mit der gleichen Zahl
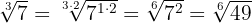
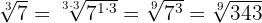
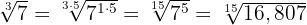
2 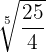
Wir multiplizieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel mit der gleichen Zahl 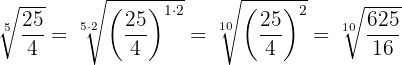
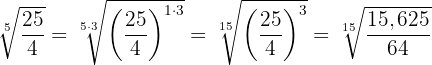
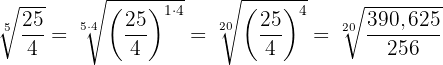
3 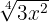
Wir multiplizieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel mit der gleichen Zahl 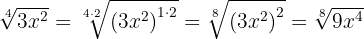
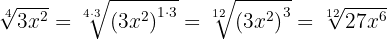
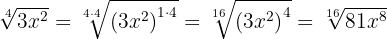
Ermittle mithilfe der Vereinfachung äquivalente Wurzeln für die folgenden Wurzeln.
1 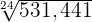
2 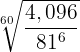
3 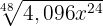
1 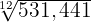
Wir dividieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel durch die gleiche Zahl
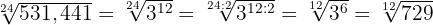
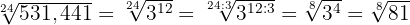
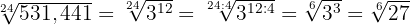
2 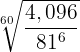
Wir dividieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel durch die gleiche Zahl 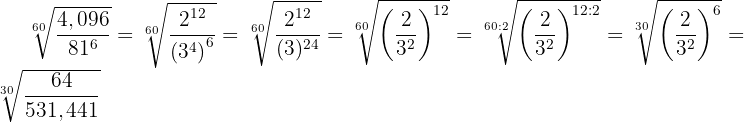
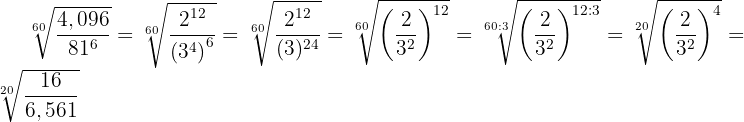
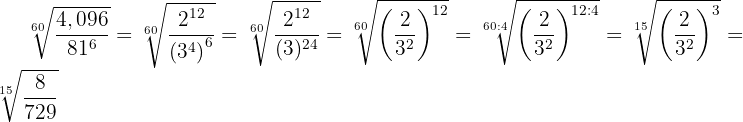
3 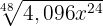
Wir dividieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel durch die gleiche Zahl 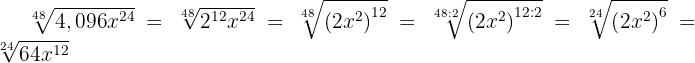
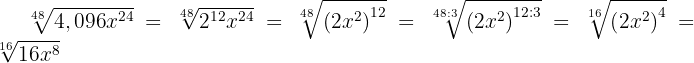
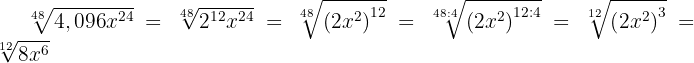
Untersuche, ob die Wurzeln 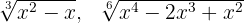 äquivalent sind.
äquivalent sind.
Wir drücken die erste Wurzel in Bruchschreibweise aus und faktorisieren hierzu den Radikanden
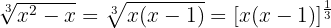
Wir drücken die zweite Wurzel in Bruchschreibweise aus und faktorisieren hierzu den Radikanden
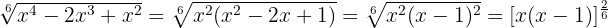
Wir untersuche, ob die gebrochenen Exponenten 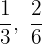 äquivalent sind
äquivalent sind
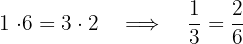 sind äquivalent
sind äquivalent
Somit sind auch die Wurzeln äquivalent.
Ermittle mithilfe der Vereinfachung eine Wurzel äquivalent zu 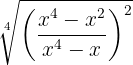 .
.
Wir müssen eine Wurzel äquivalent zu 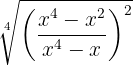 finden
finden
Wir faktorisieren den Zähler des Radikanden ohne zu quadrieren
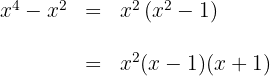
Wir faktorisieren den Nenner des Radikanden ohne zu quadrieren
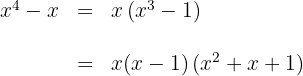
Wir vereinfachen den Radikanden ohne zu quadrieren
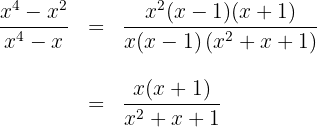
Wir schreiben die Wurzel mit ihrem vereinfachten Radikanden

Somit sind die Wurzeln äquivalent.
Ermittle mithilfe der Vereinfachung eine Wurzel äquivalent zu 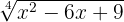 .
.
Wir möchten eine äquivalente Wurzel zu 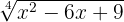 finden
finden
Wir faktorisieren den Radikanden
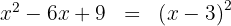
Wir schreiben die Wurzel mit ihrem vereinfachten Radikanden
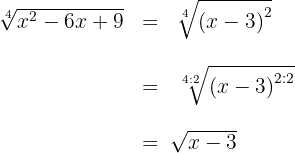
Somit sind die Wurzel äquivalent.
Gib an, ob die Wurzel 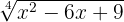 nicht kürzbar ist.
nicht kürzbar ist.
Wir faktorisieren den Radikanden
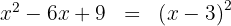
Wir schreiben die Wurzel als Bruch
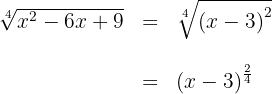
Der Bruch der Potenz ist nicht kürzbar und somit ist die Wurzel ebenfalls nicht kürzbar
Gib an, ob die Wurzel 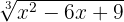 nicht kürzbar ist.
nicht kürzbar ist.
Wir faktorisieren den Radikanden
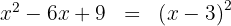
Wir schreiben die Wurzel als Bruch
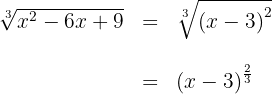
Der Bruch der Potenz ist nicht kürzbar und somit ist die Wurzel ebenfalls nicht kürzbar
Ermittle mithilfe der Erweiterung von Wurzeln eine Wurzel äquivalent zu 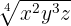 .
.
Wir müssen eine Wurzel äquivalent zu 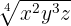 finden, indem wir die Erweiterung von Wurzeln anwenden
finden, indem wir die Erweiterung von Wurzeln anwenden
Wir multiplizieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel mit der gleichen Zahl
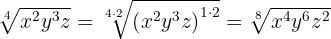
Ermittle mithilfe der Vereinfachung von Wurzeln eine Wurzel äquivalent zu 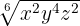 .
.
Wir müssen eine Wurzel äquivalent zu 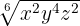 finden, indem wir die Vereinfachung von Wurzeln anwenden
finden, indem wir die Vereinfachung von Wurzeln anwenden
Wir dividieren den Exponenten des Radikanden und den Wurzelexponenten der Wurzel durch eine gleiche Zahl
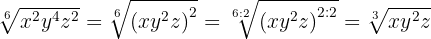
Mit KI zusammenfassen:












