Löse folgende Probleme:
1 Berechne das Volumen des Toilettenpapiers auf der folgenden Rolle. Runde auf zwei Dezimalstellen.

V = 
Dieses Feld ist erforderlich.
Zunächst ist festzustellen, dass wir zwei Volumina berechnen müssen. Das Volumen des Zylinders, der durch das Papier gebildet wird, und das Volumen des Hohlzylinders, der sich im Inneren befindet.
Anschließend subtrahieren wir den zweiten Wert vom ersten, um die genaue Menge des verfügbaren Toilettenpapiers zu berechnen.
Vollständiger Zylinder
Da der Durchmesser  cm beträgt, ist der Radius
cm beträgt, ist der Radius  cm.
cm.
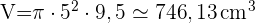
Hohlkörper
Da der Durchmesser  cm beträgt, ist der Radius
cm beträgt, ist der Radius  cm.
cm.
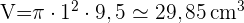
Volumen des Papiers:
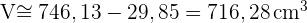
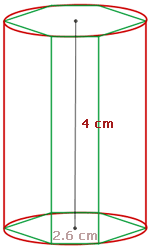
2 Berechne Volumen und Fläche eines Zylinders in einem sechseckigen Prisma mit der Basis eines regelmäßigen Sechsecks, dessen Apothema 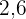 cm und dessen Höhe
cm und dessen Höhe  cm beträgt. Runde auf zwei Dezimalstellen.
cm beträgt. Runde auf zwei Dezimalstellen.
A = 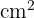
Dieses Feld ist erforderlich.
V = 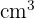
Dieses Feld ist erforderlich.
Um die Fläche und das Volumen des Zylinders zu berechnen, benötigen wir die Höhe (die wir bereits haben) und den Radius, den wir durch Anwendung des Satzes des Pythagoras erhalten.
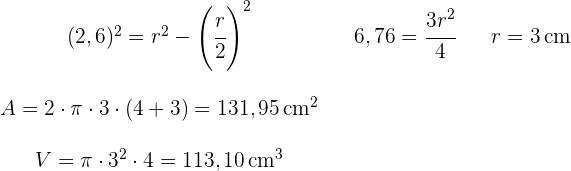
3 Berechne die Höhe einer Eistüte mit einem Durchmesser von  cm und einem Volumen von
cm und einem Volumen von 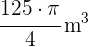 . Runde auf zwei Dezimalstellen.
. Runde auf zwei Dezimalstellen.
h = 
Dieses Feld ist erforderlich.
Wie viel Eis bräuchte man, wenn man nicht nur eine Kugel Eis in die Waffel geben, sondern die ganze Waffel füllen möchte?
V = 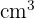
Dieses Feld ist erforderlich.
Um zu vermeiden, dass wir uns bekleckern, wird die Tüte in Papier mit der gleichen Form, aber mit 3 cm weniger Höhe eingewickelt. Wie viel Papier wird hierfür verwendet?
A = 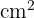
Dieses Feld ist erforderlich.
1 Wir berechnen die Höhe des Kegels anhand des Volumens:
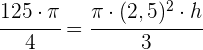
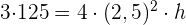
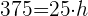

2 Das benötigte Volumen des Eises ist das oben berechnete Volumen des Kegels plus das Volumen der Halbkugel, die aus dem Kegel herausragt
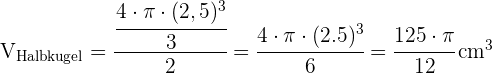
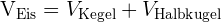
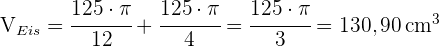
3 Die Fläche des Papiers entspricht der Fläche des Kegels, aber mit einer Höhe von 15 - 3 = 12 cm und einem Radius von 2 cm. Wir berechnen die Mantellinie des Kegels mit dem Satz des Pythagoras
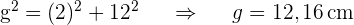
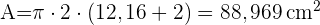
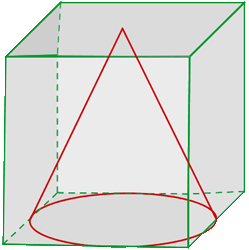
4 In einen Würfel mit einem Volumen von einem Kubikmeter führen wir einen Kegel ein, dessen Basis durch den in die Basis des Würfels eingeschriebenen Kreises markiert ist. Wenn wir den freien Raum im Würfel mit Wasser füllen, wie viel Wasser brauchen wir dann? Runde auf zwei Dezimalstellen.
V = 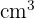
Dieses Feld ist erforderlich.
Um das benötigte Wasservolumen zu ermitteln, berechnen wir einfach das Volumen des Kegels und subtrahieren es vom Volumen des Würfels. Die Höhe des Kegels ist  m und der Radius ist
m und der Radius ist  m, da die Basis des Kegels der Kreis ist, der in die Basis des Würfels eingeschrieben ist. Die Mantellinie ergibt sich nach dem Satz des Pythagoras aus dem Radius und der Höhe.
m, da die Basis des Kegels der Kreis ist, der in die Basis des Würfels eingeschrieben ist. Die Mantellinie ergibt sich nach dem Satz des Pythagoras aus dem Radius und der Höhe.

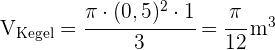
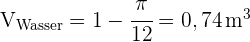
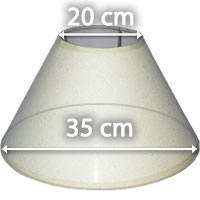
5 Wie viel Kunststoff wurde benötigt, um den Lampenschirm für die folgende Lampe herzustellen, deren Höhe  cm beträgt? Runde auf zwei Dezimalstellen.
cm beträgt? Runde auf zwei Dezimalstellen.
A = 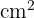
Dieses Feld ist erforderlich.
V = 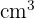
Dieses Feld ist erforderlich.
Um die benötigte Menge an Kunststoff zu berechnen, wird die Seitenfläche des Schirms berechnet, der einen Kegelstumpf darstellt. Zunächst berechnen wir die Mantellinie des Kegels mit dem Satz des Pythagoras: 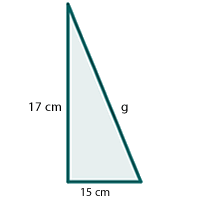
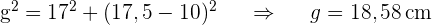
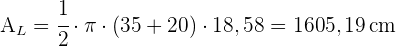
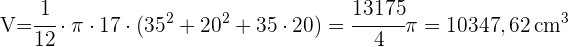
Mit KI zusammenfassen:


