Klassifiziere die Zahlen:
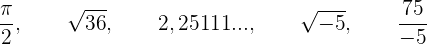
Klassifiziere die Zahlen: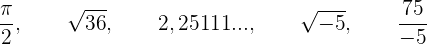
Lösungen
1. 
Wir beachten, dass  eine irrationale Zahl ist. Das heißt,
eine irrationale Zahl ist. Das heißt, 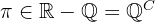 , wobei
, wobei 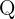 die rationalen Zahlen sind. Die Multiplikation, die Division, die Addition oder die Subtraktion einer irrationalen Zahl und einer rationalen Zahl ergibt bekanntlich eine irrationale Zahl. Somit ist
die rationalen Zahlen sind. Die Multiplikation, die Division, die Addition oder die Subtraktion einer irrationalen Zahl und einer rationalen Zahl ergibt bekanntlich eine irrationale Zahl. Somit ist  irrational
irrational

2. 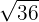
Wir sehen, dass es sich hierbei um eine vollständig ziehbare Wurzel handelt, also 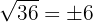 .
.  und
und  sind ganze Zahlen, weshalb
sind ganze Zahlen, weshalb
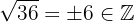
3. 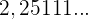
Jede Zahl, die eine periodische Dezimalstelle hat, kann als Bruch ausgedrückt werden. Das bedeutet, dass jede Zahl mit einer periodischen Dezimalstelle eine rationale Zahl ist. Tatsächlich ist 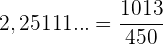 , was beweist, dass es sich um eine rationale Zahl handelt
, was beweist, dass es sich um eine rationale Zahl handelt
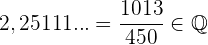
4. 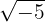
Die Wurzeln negativer Zahlen gehören nicht zu den reellen Zahlen, sondern zu einer Erweiterung der reellen Zahlen, den komplexen Zahlen 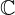 . Das heißt, diese Zahl ist eine komplexe Zahl.
. Das heißt, diese Zahl ist eine komplexe Zahl.
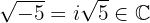
5. 
Da wir hier einen Bruch mit ganzen Zahlen haben, ist klar, dass es sich um eine rationale Zahl handelt. Wenn wir jedoch die Division durchführen, ergibt sich, dass dieser Bruch der ganzen Zahl 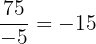 entspricht. Wir erhalten also
entspricht. Wir erhalten also
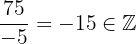
Zahlengerade
Stelle auf der Geraden dar: 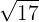
Stelle auf der Geraden dar: 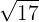
Lösung
Hierfür ziehen wir zunächst die Wurzel und erhalten
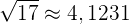
Wir zeichnen diesen Punkt auf der Geraden ein
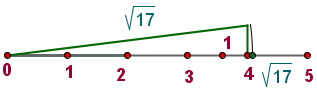
Absolutwert
Stelle auf der Zahlengeraden die Zahlen dar, die folgende Beziehungen verifizieren:

Stelle auf der Zahlengeraden die Zahlen dar, die folgende Beziehungen verifizieren:

Stelle auf der Zahlengeraden die Zahlen dar, die folgende Beziehungen verifizieren:

Lösungen:
1. 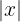 .
.


Beachte, dass durch die Definition des Absolutwerts die folgenden Gleichungen äquivalent sind

2. Die letzte Ungleichung besagt, dass  .
.

3. 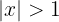
Beachte, dass durch die Definition des Absolutwerts die folgenden Gleichungen äquivalent sind
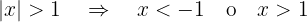 .
.
Die letzte Ungleichung besagt, dass  oder
oder 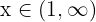 , die wir in Form der Vereinigung von Mengen ausdrücken können als
, die wir in Form der Vereinigung von Mengen ausdrücken können als 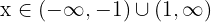 .
.
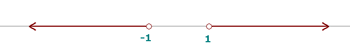
4.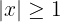
Beachte, dass durch die Definition des Absolutwerts die folgenden Gleichungen äquivalent sind
 .
.
Die letzte Ungleichung besagt, dass  oder
oder  , die wir in Form der Vereinigung von Mengen ausdrücken können als
, die wir in Form der Vereinigung von Mengen ausdrücken können als  .
.

Potenzen
Berechne die Werte der folgenden Potenzen:
a) 
b) 
c) 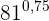
d) 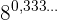
Berechne die Werte der folgenden Potenzen:
Lösungen:
a) 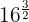
Eine Potenz mit rationalem Exponenten ist gleich einer Wurzel, deren Wurzelexponent der Nenner des Bruchs  ist und der Exponent des Radikanden ist der Zähler
ist und der Exponent des Radikanden ist der Zähler 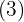 .
.
Wir zerlegen die Zahl 16 in Faktoren, führen die entsprechenden Rechenschritte im Radikanden durch und klammern Faktoren aus
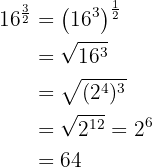
b) 
Eine Potenz mit Bruch als Exponent ist gleich einer Wurzel, deren Wurzelexponent der Nenner des Bruchs 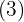 ist und der Exponent des Radikanden ist der Zähler
ist und der Exponent des Radikanden ist der Zähler  .
.
Wir zerlegen die Zahl 8 in Faktoren, führen die entsprechenden Rechenschritte im Radikanden durch und klammern Faktoren aus:

c) 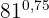
In diesem Fall wandeln wir den Exponenten, der eine exakte Dezimalzahl ist, in einen Bruch um:
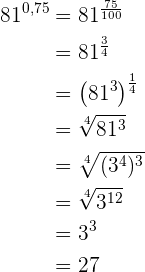
d) 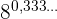
Der Exponent ist eine rein periodische Zahl. Wir können ihn also als Bruch ausdrücken: 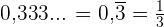 . Somit
. Somit
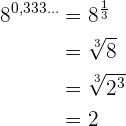
Summe von Wurzeln
Ermittle die Summen:
a) 
b) 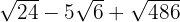
c) 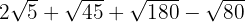
d) 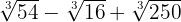
Ermittle die Summen: Wir lösen die Aufgaben, indem wir den Radikanden einfach in Potenzen von Primzahlen zerlegen. Dann werden wir mit einfacher Algebra, Addition und Subtraktion die Aufgaben lösen.
a) 
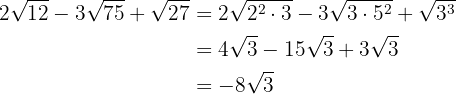
b) 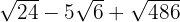
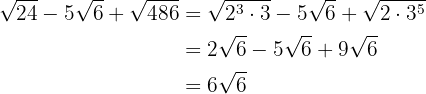
c) 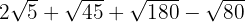
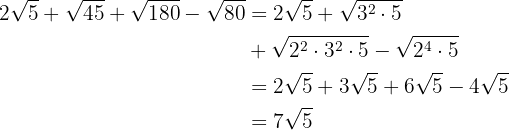
d) 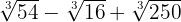
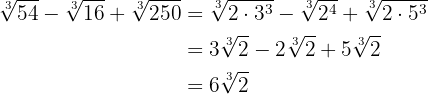
Rechnen mit Wurzeln
Berechne:
a) 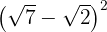
b) 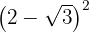
c) 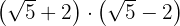
d) 
Lösungen:
Um diese Aufgabe zu lösen, wenden wir einfach die Theorie an, die wir zu Potenzen und Multiplikation von Binomen kennen.
a) 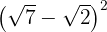
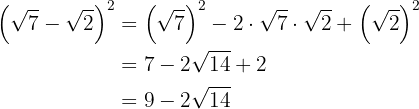
b)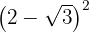
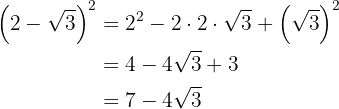
c) 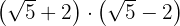
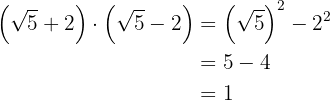
d) 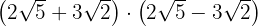
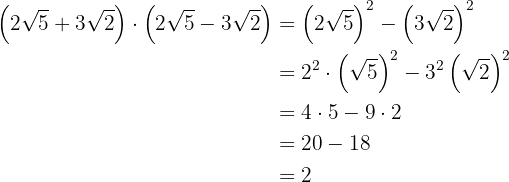
Wurzeln und Potenzen
Berechne: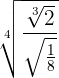
Berechne:
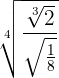
Lösung:
Um diese Aufgabe zu lösen, werden wir einen Großteil der uns bekannten Theorie zu Exponenten anwenden. Wir werden die Brüche in den Exponenten solange umformen, bis wir unseren Ausdruck entsprechend vereinfacht haben.
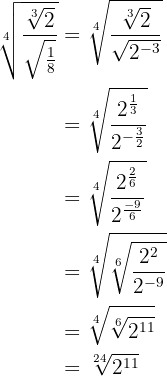
Berechne:
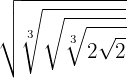
Berechne:
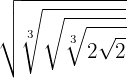
Lösung:
Um diese Aufgabe zu lösen, wenden wir die Äquivalenz von Potenzen mit rationalem Exponenten und Wurzeln an, um vereinfachen zu können:
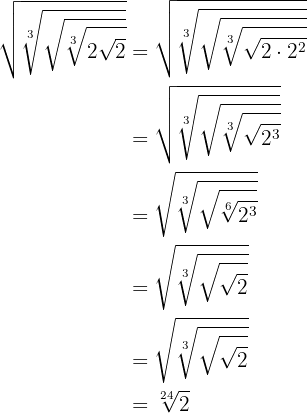
Berechne:
a) 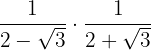
b) 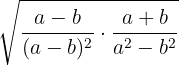
Lösungen:Wir nutzen unser algebraisches Wissen, um diese Berechnungen durchzuführen:
a) 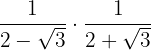
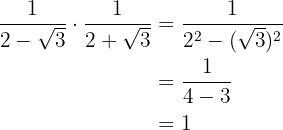
b) 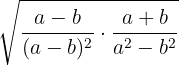
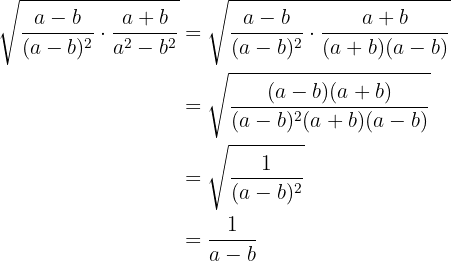
Rationalisieren
Rationalisieren
a) 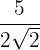
b) 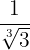
c) 
d) 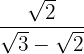
Rationalisieren:
Lösungen:
Wir beachten, dass das Rationalisieren darin besteht, die Wurzeln aus dem Nenner eines Bruchs zu eliminieren. Hierfür multiplizieren wir den Bruch mit einem geeigneten Faktor.
a) 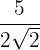
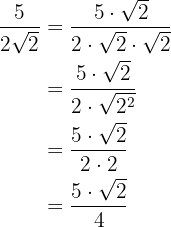
b) 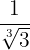
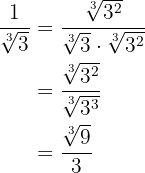
c) 
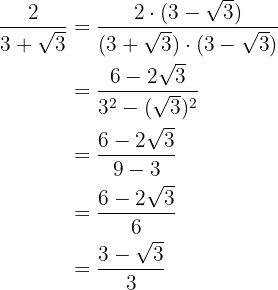
d)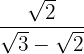
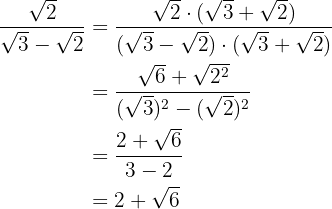
Mit KI zusammenfassen:


