Kapitel

Löse folgende Integrale
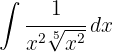
Um das Integral zu lösen, bringen wir den Nenner nach oben und vereinfachen die Potenzen. Schließlich wenden wir die Potenzregel an.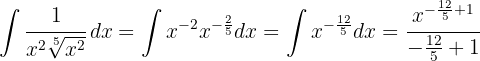
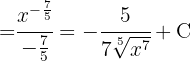
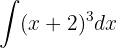
Um das Integral zu lösen, substituieren wir  und wenden die Potenzregel an.
und wenden die Potenzregel an.

Um das Integral zu lösen, substituieren wir 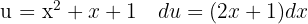 und wenden die Potenzregel an.
und wenden die Potenzregel an. 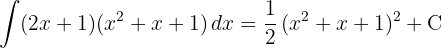

Um das Integral zu lösen, substituieren wir 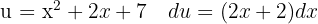 und wenden die Potenzregel an.
und wenden die Potenzregel an.
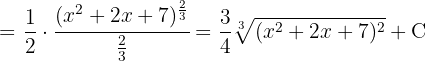
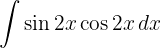
Um das Integral zu lösen, substituieren wir  und wenden die Potenzregel an.
und wenden die Potenzregel an.
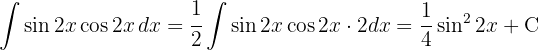
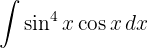
Um das Integral zu lösen, substituieren wir  und wenden die Potenzregel an.
und wenden die Potenzregel an.
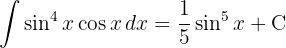
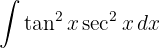
Um das Integral zu lösen, substituieren wir 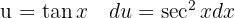 und wenden die Potenzregel an.
und wenden die Potenzregel an.
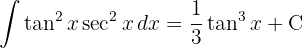
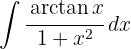
Um das Integral zu lösen, substituieren wir 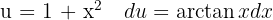 und wenden die Potenzregel an.
und wenden die Potenzregel an.
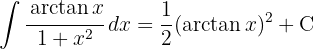
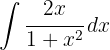
Um das Integral zu lösen, substituieren wir  und integrieren
und integrieren  .
.
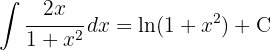
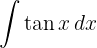
Um das Integral zu lösen, wenden wir die Tangensfunktion in Bezug auf den Sinus und den Kosinus an und integrieren schließlich  .
.


Um das Integral zu lösen, substituieren wir  und integrieren
und integrieren  .
.

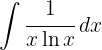
Um das Integral zu lösen, substituieren wir 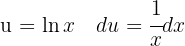 und integrieren
und integrieren  .
.
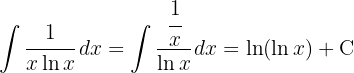

Um das Integral zu lösen, substituieren wir  und integrieren
und integrieren  .
.

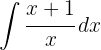
Um das Integral zu lösen, separieren wir das Integral und integrieren schließlich  .
.
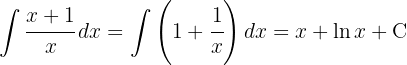
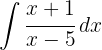
Um das Integral zu lösen, fügen wir eine Null hinzu, damit wir es in zwei Integrale aufteilen können und integrieren schließlich  .
.


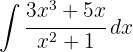
Um das Integral zu lösen, beginnen wir zunächst mit einer vereinfachten Polynomdivision, um es in zwei Integrale aufteilen zu können. Und schließlich integrieren wir  mit einer Substitution
mit einer Substitution  .
.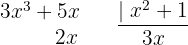
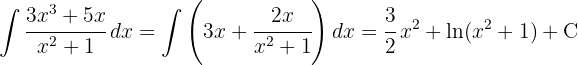
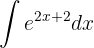
Um das Integral zu lösen, substituieren wir  und integrieren schließlich
und integrieren schließlich  .
.
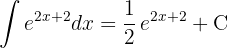

Um das Integral zu lösen, integrieren wir 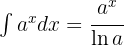 .
.

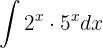
Um das Integral zu lösen, integrieren wir 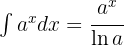 .
.
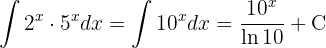
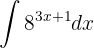
Um das Integral zu lösen, substituieren wir 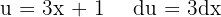 und integrieren schließlich
und integrieren schließlich 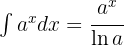 .
.
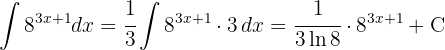
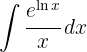
Um das Integral zu lösen, substituieren wir 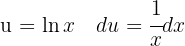 und integrieren schließlich
und integrieren schließlich  .
.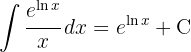 .
.

Um das Integral zu lösen, substituieren wir  und integrieren schließlich
und integrieren schließlich  .
.

Um das Integral zu lösen, substituieren wir 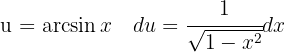 und integrieren schließlich
und integrieren schließlich  .
.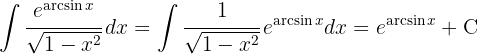
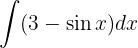
Wir beginnen, indem wir das Integral aufteilen und integrieren jeweils 


Wir beginnen, indem wir substituieren 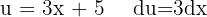 und integrieren schließlich
und integrieren schließlich 


Wir beginnen, indem wir substituieren 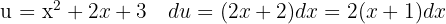 und integrieren schließlich
und integrieren schließlich 
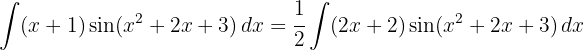
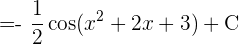
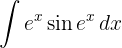
Wir beginnen, indem wir substituieren 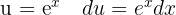 und integrieren schließlich
und integrieren schließlich 


Wir beginnen, indem wir substituieren  und integrieren schließlich
und integrieren schließlich 


Wir beginnen, indem wir  anwenden, teilen das Integral auf und integrieren schließlich
anwenden, teilen das Integral auf und integrieren schließlich  . Wir substituieren
. Wir substituieren  .
.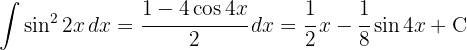
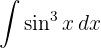
Wir beginnen, indem wir den Sinus aufteilen und wenden die trigonometrische Funktion 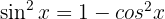 an. Schließlich integrieren wir
an. Schließlich integrieren wir  und substituieren
und substituieren 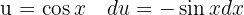
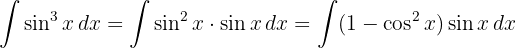
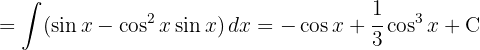
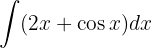
Wir teilen das Integral auf und integrieren schließlich 

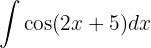
Wir beginnen, indem wir substituieren 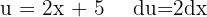 und integrieren schließlich
und integrieren schließlich 
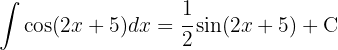
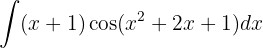
Wir beginnen, indem wir substituieren 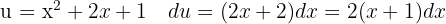 und integrieren schließlich
und integrieren schließlich
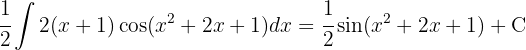

Wir beginnen, indem wir substituieren  und integrieren schließlich
und integrieren schließlich 


Wir wenden die trigonometrische Funktion 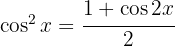 an, teilen das Integral auf und integrieren schließlich
an, teilen das Integral auf und integrieren schließlich  . Wir substituieren
. Wir substituieren 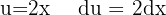

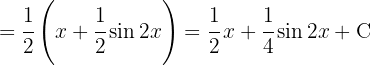

Wir wenden die trigonometrische Funktion 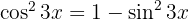 an, teilen das Integral auf und integrieren
an, teilen das Integral auf und integrieren  . Wir substituieren
. Wir substituieren 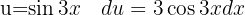


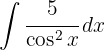
Wir wenden die trigonometrische Funktion 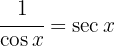 an und integrieren schließlich
an und integrieren schließlich 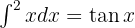 }
}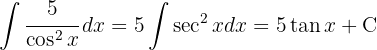
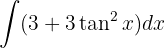
Wir wenden die trigonometrische Funktion  an und integrieren schließlich
an und integrieren schließlich 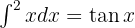 }
} 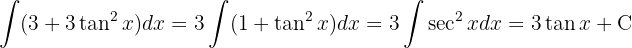

Wir beginnen, indem wir substituieren  und integrieren schließlich
und integrieren schließlich 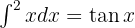 }
} 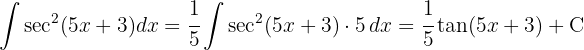

Wir teilen den Sekans auf und wenden die trigonometrische Funktion  an, integrieren
an, integrieren 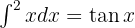 und substituieren
und substituieren 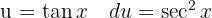
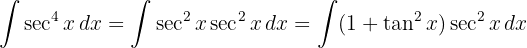

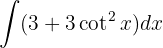
Um das Integral zu lösen, wenden wir die trigonometrische Funktion 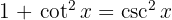 an und integrieren schließlich
an und integrieren schließlich 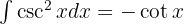
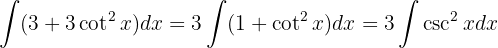
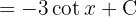

Wir beginnen mit dem Hinzufügen einer Null, wenden die trigonometrische Funktion  an, teilen das Integral auf und integrieren schließlich
an, teilen das Integral auf und integrieren schließlich 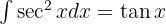
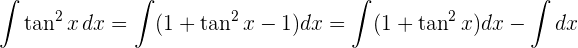
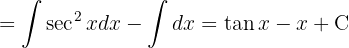
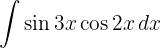
Um das Integral zu lösen, bestimmen wir die Werte für A und B, die folgende Gleichung erfüllen

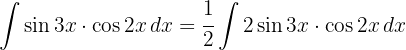
Wir substituieren 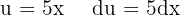 und integrieren schließlich
und integrieren schließlich 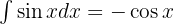
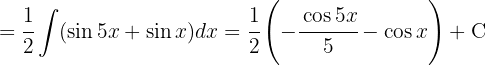
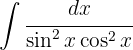
Um das Integral zu lösen, wenden wir die trigonometrische Funktion  an, teilen das Integral auf und vereinfachen
an, teilen das Integral auf und vereinfachen

Nun wenden wir 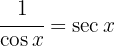 und
und 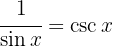 an und integrieren schließlich
an und integrieren schließlich  und
und 
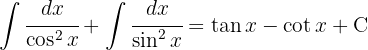
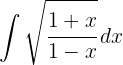
Um das folgende Integral zu lösen, multiplizieren wir Zähler und Nenner mit  und teilen das Integral auf
und teilen das Integral auf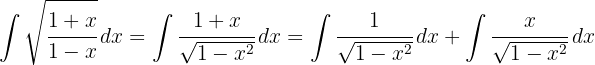
Wir integrieren  und substituieren
und substituieren 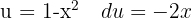
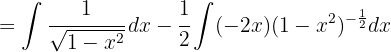


Um das folgende Integral zu lösen, multiplizieren wir Zähler und Nenner mit 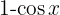 , berechnen das Binom zum Quadrat, wenden
, berechnen das Binom zum Quadrat, wenden 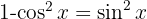 an und teilen das Integral auf
an und teilen das Integral auf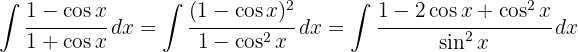
Nun wenden wir 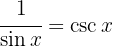 an, integrieren
an, integrieren  , substituieren
, substituieren 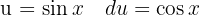 und fügen eine Null hinzu, um
und fügen eine Null hinzu, um 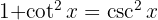 anwenden zu können und schließlich das Integral
anwenden zu können und schließlich das Integral 



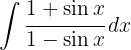
Um das folgende Integral zu lösen, multiplizieren wir Zähler und Nenner mit 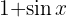 , berechnen das Binom zum Quadrat, wenden
, berechnen das Binom zum Quadrat, wenden 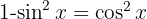 an und teilen das Integral auf
an und teilen das Integral auf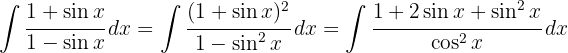

Nun wenden wir 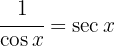 an, integrieren
an, integrieren 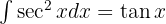 , substituieren
, substituieren 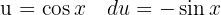 und fügen eine Null hinzu, um
und fügen eine Null hinzu, um 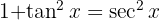 anwenden zu können
anwenden zu können
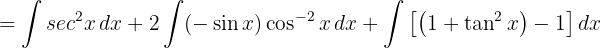
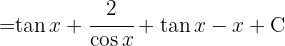
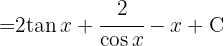

Um das folgende Integral zu lösen, müssen wir so vervollständigen, damit wir ein Integral der Form 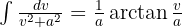 erhalten, wobei
erhalten, wobei 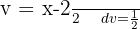 .
.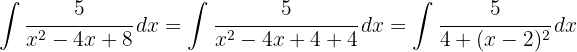
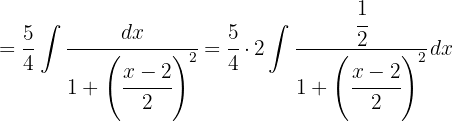
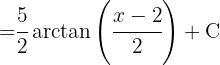

Wir teilen das Integral auf und substituieren auf einer Seite  . Auf der anderen Seite möchten wir ein Integral der Form
. Auf der anderen Seite möchten wir ein Integral der Form 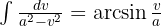 erhalten, wobei
erhalten, wobei 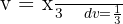 .
.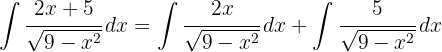
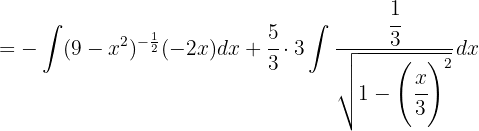


Wir möchten ein Integral der Form 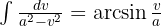 erhalten, wobei
erhalten, wobei  .
.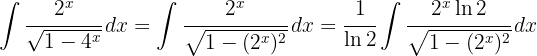
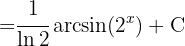
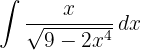
Wir möchten ein Integral der Form 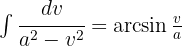 erhalten und gehen im Nenner wie folgt vor:
erhalten und gehen im Nenner wie folgt vor:
donde 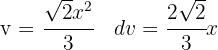 .
.

Mit KI zusammenfassen:













