Willkommen in unserem Abschnitt, der der Berechnung von Funktionsvolumina mithilfe der Integralrechnung gewidmet ist. Dieses Thema ist in der Mathematik und Physik von großer Bedeutung und seine Beherrschung ist für die Lösung zahlreicher Probleme im Zusammenhang mit Flächen und Volumen im dreidimensionalen Raum unerlässlich. In diesem Leitfaden führen wir dich Schritt für Schritt durch die Berechnung von Volumen mithilfe von Integraltechniken.
Bei der Berechnung des Volumens einer Funktion wird ein dreidimensionaler Festkörper in infinitesimale Elemente unterteilt, und diese Elemente werden mit Hilfe definitiver Integrale addiert, um das Gesamtvolumen zu ermitteln. Dies ermöglicht es uns, die Ausdehnung von Objekten im dreidimensionalen Raum genau zu verstehen und zu quantifizieren.
Beginnen wir mit der Berechnung von Integralen!
Das Volumen des Rotationskörpers, der durch Rotation der Kurve  um die x-Achse entsteht und durch
um die x-Achse entsteht und durch  und
und 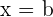 begrenzt wird, ist gegeben durch:
begrenzt wird, ist gegeben durch:
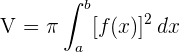
Finde das Volumen des Kegelstumpfes, der durch Rotation um  die durch
die durch 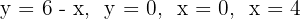 begrenzte Fläche entsteht.
begrenzte Fläche entsteht.
1 Wir stellen das Problem grafisch dar
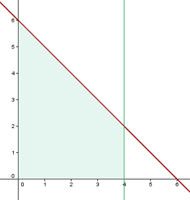
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln

3 Um das Integral zu lösen, betrachten wir die Substitution 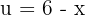 und berechnen ihre Ableitung
und berechnen ihre Ableitung
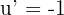
4 Wir benutzen die Integrationsformel

5 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten

6 Wir werten an den Extrema der Integration aus
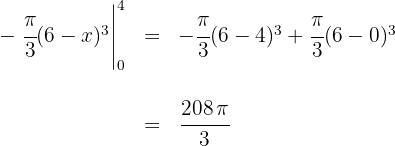
Somit ist das Volumen 
Ermittle das Volumen der Flächen, die von dem Graphen 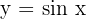 und den Geraden
und den Geraden 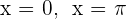 begrenzt werden, wenn sie um die x-Achse rotieren
begrenzt werden, wenn sie um die x-Achse rotieren
1 Wir stellen das Problem grafisch dar
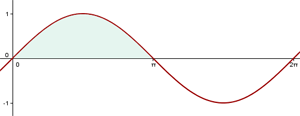
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln
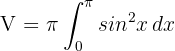
3 Um das Integral zu berechnen, sehen wir uns die trigonometrische Identität 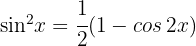 an. Daher wird das Integral wie folgt ausgedrückt
an. Daher wird das Integral wie folgt ausgedrückt
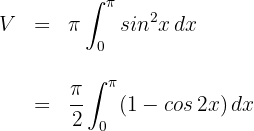
4 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
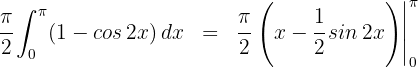
5 Wir werten an den Extrema der Integration aus
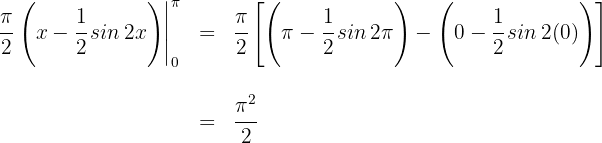
Somit ist das Volumen 
Berechne das Volumen, das von einer Halbwelle der Sinuskurve 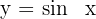 erzeugt wird, wenn sie um die x-Achse rotiert.
erzeugt wird, wenn sie um die x-Achse rotiert.
1 Wir stellen das Problem grafisch dar
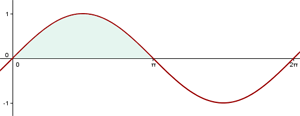
Wir stellen fest, dass die Sinuskurve der Abbildung in Übung 2 entspricht.
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln
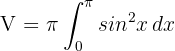
3 Um das Integral zu berechnen, sehen wir uns die trigonometrische Identität 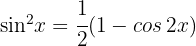 an. Daher wird das Integral wie folgt ausgedrückt
an. Daher wird das Integral wie folgt ausgedrückt
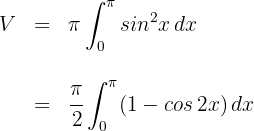
4 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
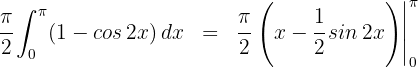
5 Wir werten an den Extrema der Integration aus
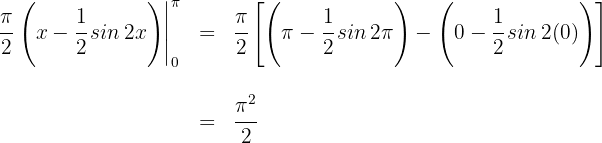
Somit ist das Volumen 
Ermittle das Volumen des Rotationskörpers, der um die x-Achse rotiert, und durch die Funktion  , die x-Achse und die Geraden
, die x-Achse und die Geraden 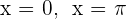 bestimmt wird.
bestimmt wird.
1 Wir setzen in die Formel ein, um das Volumen zu ermitteln

2 Wir arbeiten mit dem Integranden
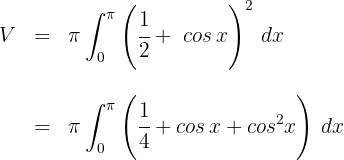
3 Wir betrachten die trigonometrische Identität 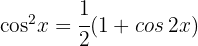 . Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
. Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten

4 Wir werten an den Extrema der Integration aus
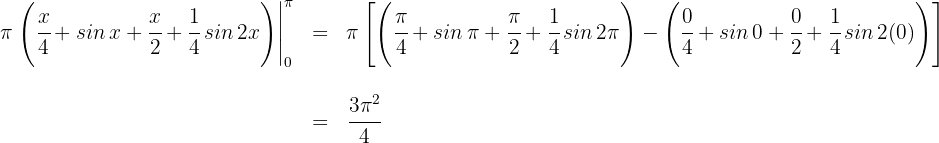
Somit ist das Volumen 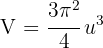
Ermittle das Volumen, das der Kreis  bei einer Drehung um die x-Achse hat.
bei einer Drehung um die x-Achse hat.
1 Wir drücken die Kreisgleichung in ihrer allgemeinen Form aus
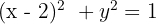
2 Der Mittelpunkt des Kreises ist  und der Radius ist
und der Radius ist 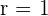 . Die Schnittpunkte mit der x-Achse lauten:
. Die Schnittpunkte mit der x-Achse lauten:
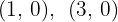
3 Anhand der allgemeinen Kreisgleichung erhalten wir die Funktion
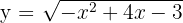
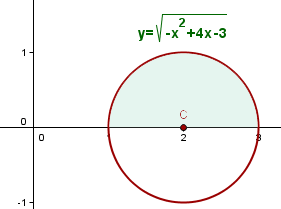
4 Wir setzen in die Formel ein, um das Volumen zu ermitteln

5 Wir arbeiten mit dem Integranden

6 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
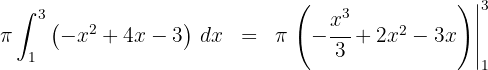
7 Wir werten an den Extrema der Integration aus
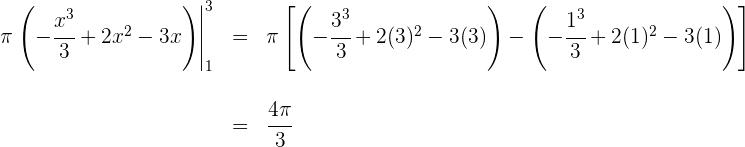
Somit ist das Volumen 
Berechne das Volumen, das durch die Drehung des durch die Graphen von 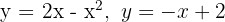 begrenzten Raums um die x-Achse entsteht.
begrenzten Raums um die x-Achse entsteht.
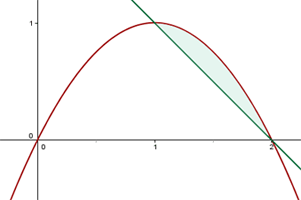
1 Um die Schnittpunkte der Geraden und der Parabel zu finden, lösen wir das System
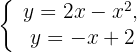
Wir setzen gleich und faktorisieren
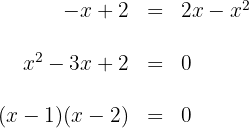
Die Nullstellen sind 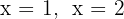 . Somit lauten die Schnittpunkte:
. Somit lauten die Schnittpunkte: 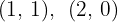
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln
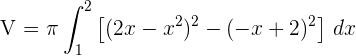
3 Wir arbeiten mit dem Integranden
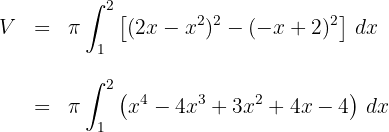
4 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
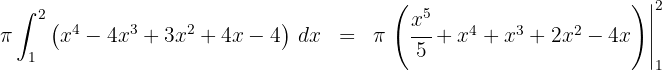
5 Wir werten an den Extrema der Integration aus
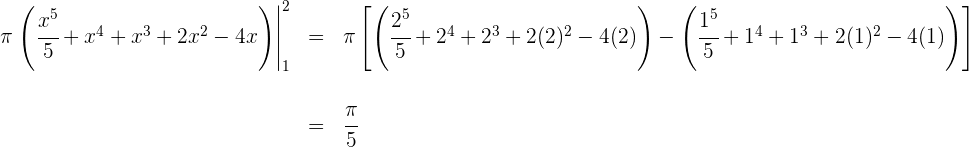
Somit ist das Volumen 
Berechne das Volumen des Körpers, der durch die Drehung des durch die Graphen von  begrenzten Raums um die x-Achse entsteht.
begrenzten Raums um die x-Achse entsteht.
1 Um die Schnittpunkte der Geraden und der Parabel zu finden, lösen wir das System

Wir setzen gleich und faktorisieren
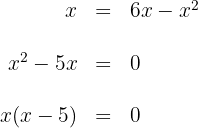
Die Nullstellen sind 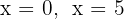 . Und somit lauten die Schnittpunkte:
. Und somit lauten die Schnittpunkte: 
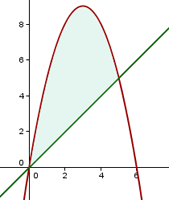
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln

3 Wir arbeiten mit dem Integranden

4 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten

5 Wir werten an den Extrema der Integration aus
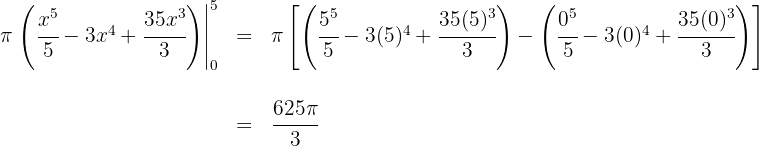
Somit ist das Volumen 
Berechne das Volumen eines Dreiecks mit den Eckpunkten  bei einer Drehung von
bei einer Drehung von  um die x-Achse.
um die x-Achse.
1 Wir stellen grafisch dar
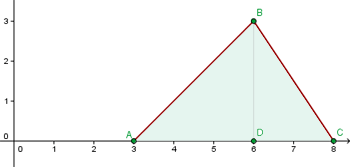
Die Gleichungen der Geraden durch  und
und  lauten
lauten
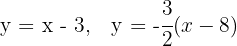
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln. Wir stellen fest, dass wir für den Streckenabschnitt  das Intervall
das Intervall 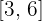 und für den Streckenabschnitt
und für den Streckenabschnitt  das Intervall
das Intervall 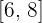 berücksichtigen müssen.
berücksichtigen müssen.
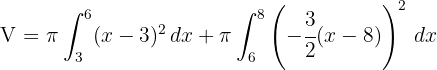
3 Wir arbeiten mit dem Integranden
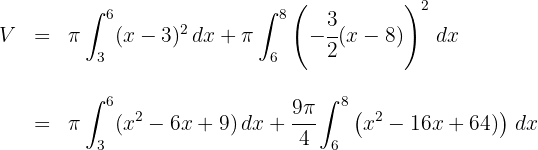
4 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
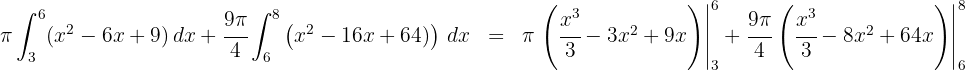
5 Wir werten an den Extrema der Integration aus

Somit ist das Volumen 
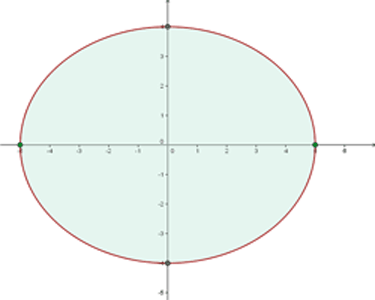
Ermittle das Volumen der Figur, die durch Rotation der Ellipse  um die x-Achse entsteht.
um die x-Achse entsteht.
1 Wir stellen grafisch dar
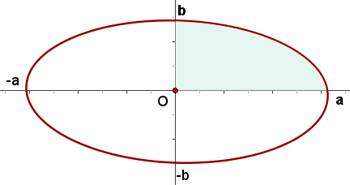
2 Der Mittelpunkt der Ellipse ist 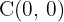 . Die Schnittpunkte mit der x-Achse lauten:
. Die Schnittpunkte mit der x-Achse lauten:
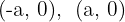
3 Aus der Gleichung der Ellipse ergibt sich die Funktion
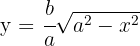
Da es sich bei der Ellipse um eine symmetrische Kurve handelt, ist das angegebene Volumen das Zweifache des Volumens, das durch den Bogen zwischen  und
und  entsteht.
entsteht.
4 Wir setzen in die Formel ein, um das Volumen zu ermitteln
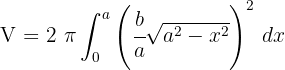
5 Wir arbeiten mit dem Integranden
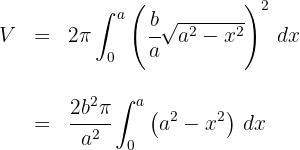
6 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
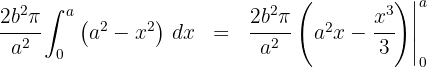
7 Wir werten an den Extrema der Integration aus
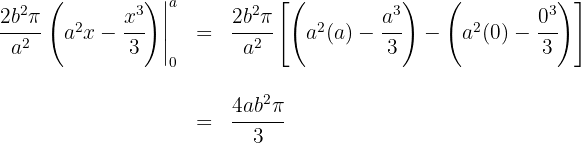
Somit ist das Volumen 
Berechne das Volumen des Zylinders, der durch das Rechteck gebildet wird, das durch die Geraden 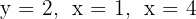 und die x-Achse begrenzt wird, wenn er um diese Achse rotiert.
und die x-Achse begrenzt wird, wenn er um diese Achse rotiert.
1 Wir setzen in die Formel ein, um das Volumen zu ermitteln
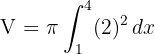
2 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
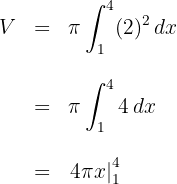
3 Wir werten an den Extrema der Integration aus
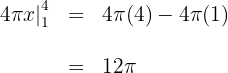
Somit ist das Volumen 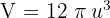
Berechne das Volumen der Kugel mit dem Radius  .
.
1 Wir gehen von der Kreisgleichung  aus
aus
2 Die Drehung eines Halbkreises um die x-Achse ergibt eine Kugel
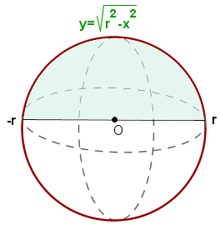
3 Aus der Kreisgleichung ergibt sich die Funktion

4 Wir setzen in die Formel ein, um das Volumen zu ermitteln
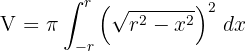
5 Wir arbeiten mit dem Integranden
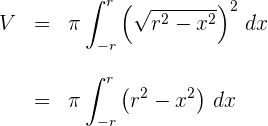
6 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
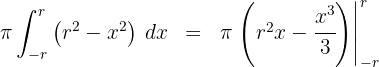
7 Wir werten an den Extrema der Integration aus
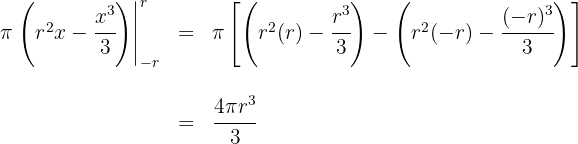
Somit ist das Volumen 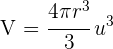
Berechne das Volumen, das durch die Drehung der durch die Parabel  und die Gerade
und die Gerade  begrenzten Fläche um die y-Achse entsteht.
begrenzten Fläche um die y-Achse entsteht.
1 Wir stellen grafisch dar
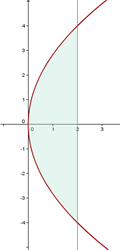
Da sie sich um die y-Achse dreht, wenden wir an:
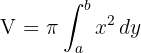
Das Volumen ergibt sich aus der Differenz zwischen dem Volumen der Geraden und dem Volumen der Parabel zwischen den Extrema  .
.
Da die Parabel symmetrisch zur x-Achse ist, ist das Volumen gleich dem doppelten Volumen, das zwischen  entsteht.
entsteht.
2 Wir setzen in die Formel ein, um das Volumen zu ermitteln
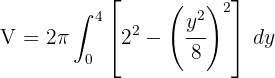
3 Da es sich um ein bestimmtes Integral handelt, können wir auf die Integrationskonstante verzichten
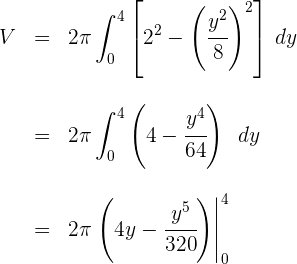
4 Wir werten an den Extrema der Integration aus

Somit ist das Volumen 
Ermittle das Volumen des Ellipsoids, das durch die Ellipse 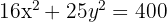 erzeugt wird, wenn sie um die x-Achse rotiert.
erzeugt wird, wenn sie um die x-Achse rotiert.
1 Wir drücken die Ellipse in ihrer allgemeinen Gleichung aus

2 Der Mittelpunkt der Ellipse ist 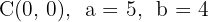 . Wir wenden die Formel aus Aufgabe 9 an
. Wir wenden die Formel aus Aufgabe 9 an

3 Wir setzen die uns bekannten Werte ein und erhalten
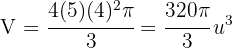
Ermittle das Volumen des Rotationskörpers, der durch Rotation der Funktion 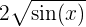 , definiert auf dem Intervall
, definiert auf dem Intervall  $[0,\pi]$[/latex, um die x-Achse entsteht.
$[0,\pi]$[/latex, um die x-Achse entsteht.
1 Wir stellen die Funktion grafisch dar.
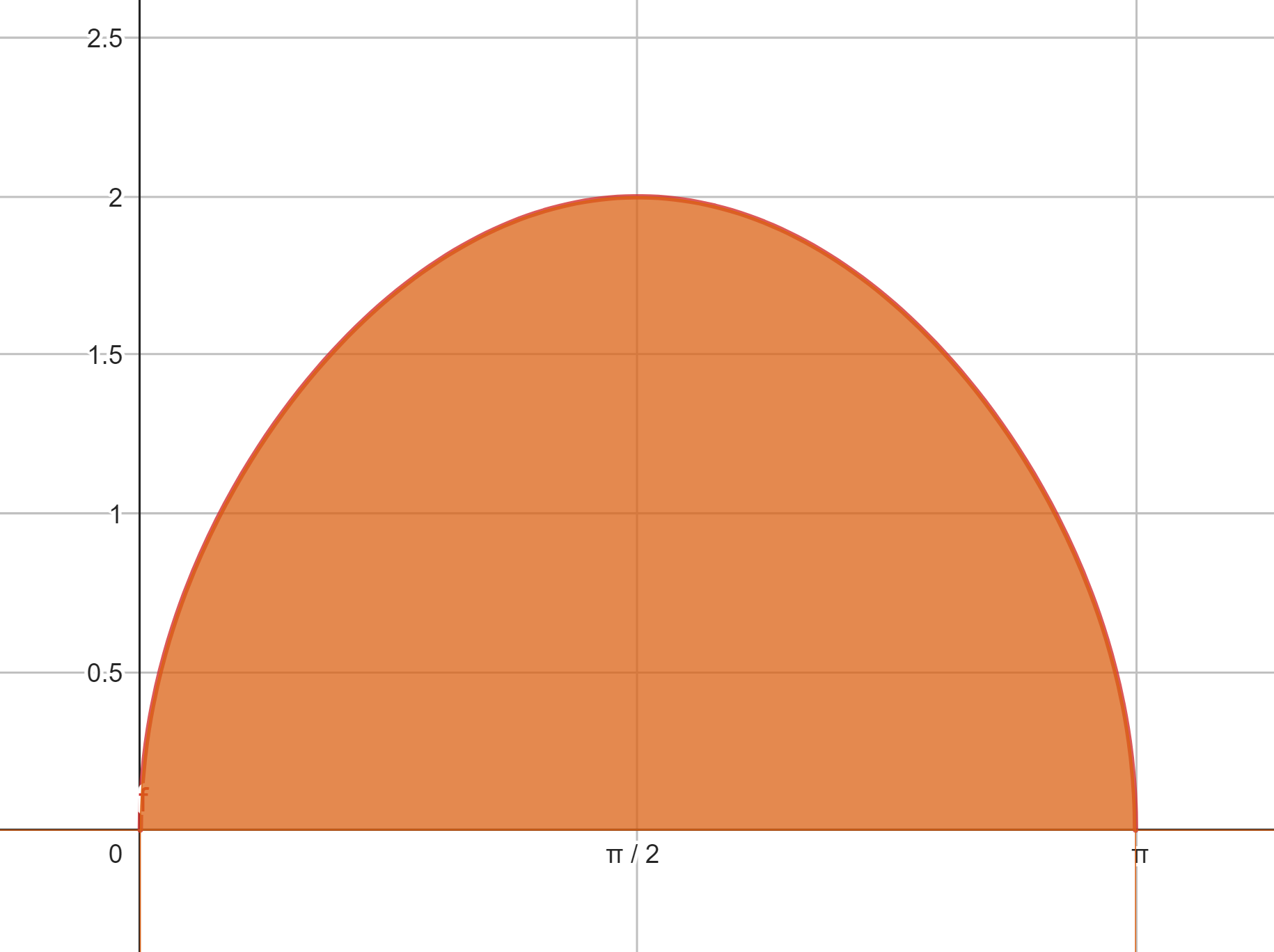
2 Wir berechnen das Integral:
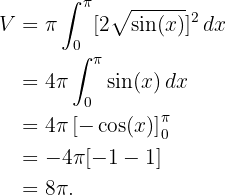
Gegeben sei  für
für 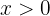 .
.
a Zeichne den Graphen von 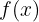 .
.
b Berechne die Fläche des Bereichs, der durch 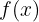 und die x-Achse auf dem Intervall
und die x-Achse auf dem Intervall 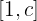 begrenzt wird, wobei
begrenzt wird, wobei  .
.
c Berechne das Volumen des Rotationskörpers, der durch Rotation des Bereichs von (b) um die x-Achse entsteht.
d Was passiert mit der Fläche, die du in (b) berechnet hast, wenn 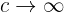 ? Was passiert mit dem Volumen des Rotationskörpers?
? Was passiert mit dem Volumen des Rotationskörpers?
a
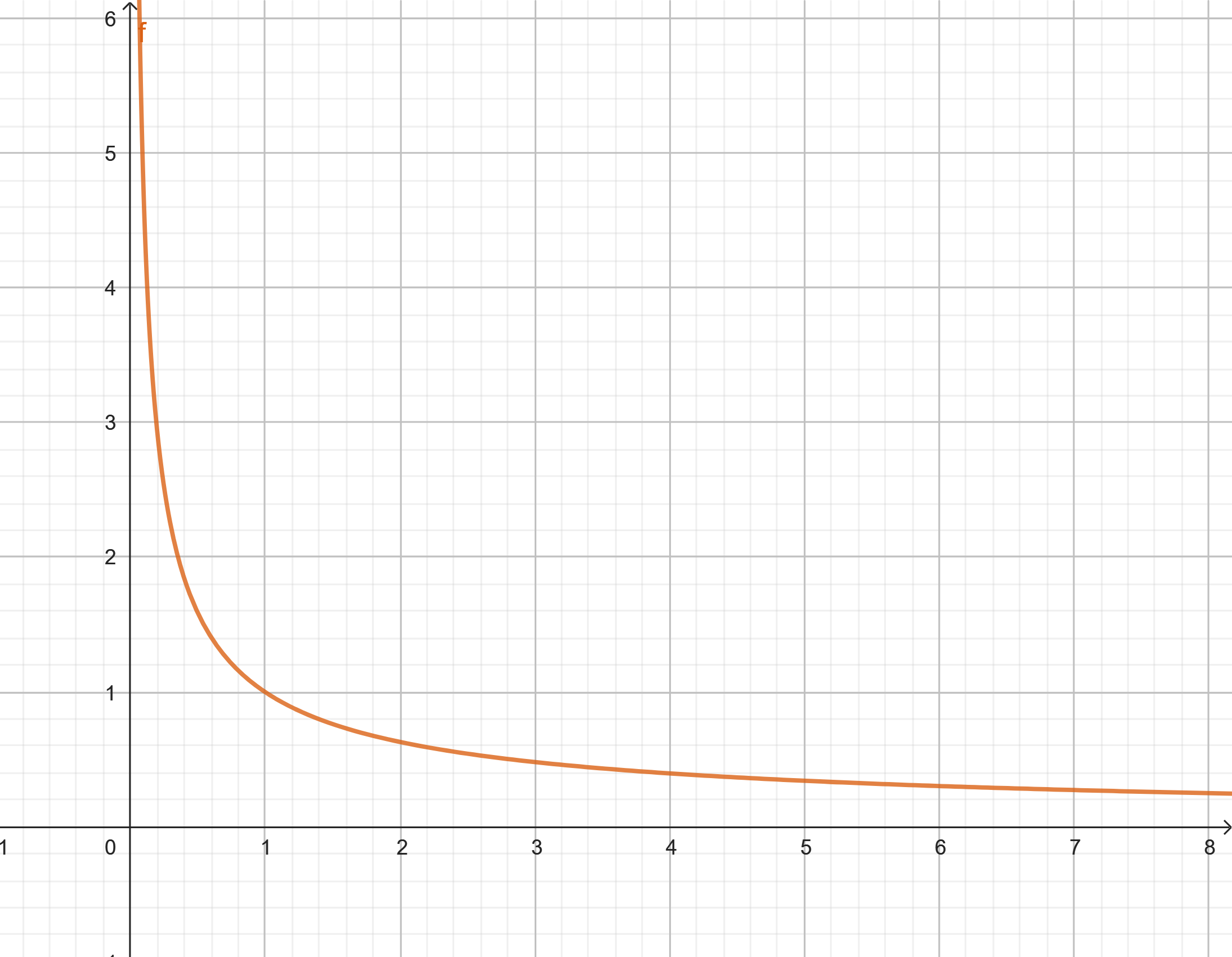
b Wir berechnen das Integral auf dem Intervall 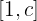 . Das heißt, die Fläche unter dem Graphen:
. Das heißt, die Fläche unter dem Graphen:
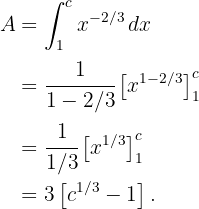
c Jetzt drehen wir denselben Bereich um die x-Achse:
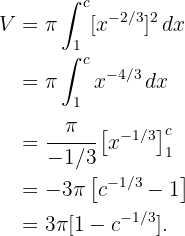
d Wenn 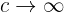 im Ergebnis von (b) enthalten ist, ergibt sich
im Ergebnis von (b) enthalten ist, ergibt sich
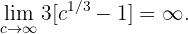
Das heißt, die Fläche unter dem Graphen geht ins Unendliche, wenn das Intervall, das wir nehmen, ins Unendliche geht. Beachte jedoch, dass
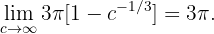
Das heißt, das Volumen des Festkörpers bleibt beschränkt.
Mit KI zusammenfassen:


