Aufgaben zur Warscheinlichkeit für eine Gruppe von Lesern
Der neueste Roman eines Autors war ein großer Erfolg, so dass 80 % der Leser ihn bereits gelesen haben.
Eine Gruppe von 4 Freunden liest sehr gerne:
1 Wie hoch ist die Wahrscheinlichkeit, dass 2 Personen der Gruppe das Buch gelesen haben?
2 Und höchstens 2?
Der neueste Roman eines Autors war ein großer Erfolg, so dass 80 % der Leser ihn bereits gelesen haben.
Eine Gruppe von 4 Freunden liest sehr gerne:
1 Wie hoch ist die Wahrscheinlichkeit, dass 2 Personen der Gruppe das Buch gelesen haben?
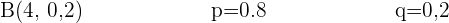
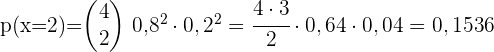
2 Und höchstens 2?

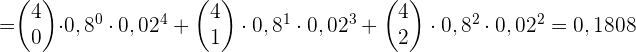
Lebenswahrscheinlichkeiten für Versicherungspolicen
Ein Versicherungsvertreter verkauft Versicherungspolicen an fünf Personen gleichen Alters und bei guter Gesundheit.
Nach den aktuellen Statistiken beträgt die Wahrscheinlichkeit, dass eine Person in diesem Zustand 30 Jahre oder länger lebt, 2/3.
Berechne die Wahrscheinlichkeit, dass sie nach 30 Jahren noch leben:
1 Die fünf Personen
2 Mindestens drei Personen
3 Genau zwei Personen
Ein Versicherungsvertreter verkauft Versicherungspolicen an fünf Personen gleichen Alters und bei guter Gesundheit.
Nach den aktuellen Statistiken beträgt die Wahrscheinlichkeit, dass eine Person in diesem Zustand 30 Jahre oder länger lebt, 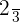 .
.
Berechne die Wahrscheinlichkeit, dass sie nach 30 Jahren noch leben:
1 Die fünf Personen
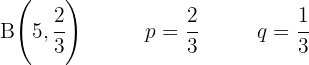
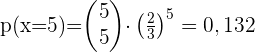
2 Mindestens 3 Personen
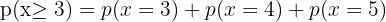
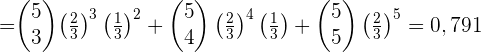
3 Genau zwei Personen
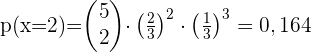
Werfen einer Münze und Wahrscheinlichkeit
Eine Münze wird 4 Mal geworfen.
Berechne die Wahrscheinlichkeit, dass Kopf öfter als Zahl geworfen wird.
Eine Münze wird 4 Mal geworfen.
Berechne die Wahrscheinlichkeit, dass Kopf öfter als Zahl geworfen wird.
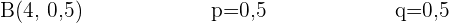
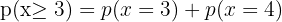
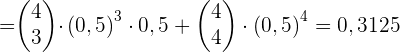
Zufallswahl, Verbundwahrscheinlichkeit
Es wird angenommen, dass zwischen 18:00 Uhr und 19:00 Uhr von fünf Telefonnummern bei einer die Leitung besetzt ist.
Wie hoch ist die Wahrscheinlichkeit, dass bei der Wahl von 10 zufällig ausgewählten Telefonnummern nur zwei besetzt sind?
Es wird angenommen, dass zwischen 18:00 Uhr und 19:00 Uhr von fünf Telefonnummern bei einer die Leitung besetzt ist.
Wie hoch ist die Wahrscheinlichkeit, dass bei der Wahl von 10 zufällig ausgewählten Telefonnummern nur zwei besetzt sind?

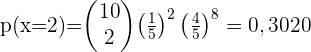
Berechnung der Wahrscheinlichkeit beim Schießen
Die Wahrscheinlichkeit, dass ein Mann beim Schießen ins Schwarze trifft, liegt bei  .
.
Wenn 10 Mal geschossen wird,
1 Wie hoch ist die Wahrscheinlichkeit, dass genau dreimal getroffen wird?
2 Wie hoch ist die Wahrscheinlichkeit, dass mindestens einmal getroffen wird?
Die Wahrscheinlichkeit, dass ein Mann beim Schießen ins Schwarze trifft, liegt bei  .
.
Wenn 10 Mal geschossen wird,
1 Wie hoch ist die Wahrscheinlichkeit, dass genau dreimal getroffen wird?

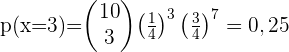
2 Wie hoch ist die Wahrscheinlichkeit, dass mindestens einmal getroffen wird?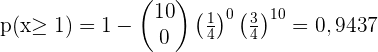
Wahrscheinlichkeit für Verkehrsdelikte
Bei Alkoholtests wurde festgestellt, dass 5 % der kontrollierten Fahrer positiv getestet wurden und dass 10 % der kontrollierten Fahrer nicht angeschnallt waren.
Es wurde auch festgestellt, dass die beiden Verstöße unabhängig voneinander auftreten.
Ein Verkehrspolizist kontrolliert fünf zufällig ausgewählte Fahrer. Wir müssen beachten, dass die Anzahl der Fahrer wichtig ist, um abschätzen zu können, dass sich der Anteil der Verstöße bei der Auswahl nicht verändert.
1 Ermittle die Wahrscheinlichkeit, dass genau drei Fahrer einen der beiden Verstöße begangen haben.
2 Ermittle die Wahrscheinlichkeit, dass mindestens einer der kontrollierten Fahrer einen der beiden Verstöße begangen hat.
Bei Alkoholtests wurde festgestellt, dass 5 % der kontrollierten Fahrer positiv getestet wurden und dass 10 % der kontrollierten Fahrer nicht angeschnallt waren.
Es wurde auch festgestellt, dass die beiden Verstöße unabhängig voneinander auftreten.
Ein Verkehrspolizist kontrolliert fünf zufällig ausgewählte Fahrer.
Wir müssen beachten, dass die Anzahl der Fahrer wichtig ist, um abschätzen zu können, dass sich der Anteil der Verstöße bei der Auswahl nicht verändert.
1 Ermittle die Wahrscheinlichkeit, dass genau drei Fahrer einen der beiden Verstöße begangen haben.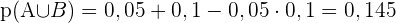
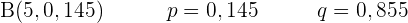
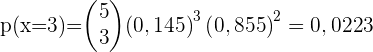
2 Ermittle die Wahrscheinlichkeit, dass mindestens einer der kontrollierten Fahrer einen der beiden Verstöße begangen hat.
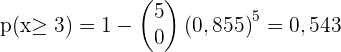
Qualitätskontrolle: Fehlerwahrscheinlichkeit
Die Wahrscheinlichkeit, dass ein produzierter Artikel fehlerhaft ist liegt bei p = 0,02.
Es werden 10.000 Artikel an verschiedene Lager verschickt.
Ermittle die erwartete Anzahl der fehlerhaften Artikel, die Varianz und die Standardabweichung.
Die Wahrscheinlichkeit, dass ein produzierter Artikel fehlerhaft ist liegt bei p = 0,02.
Es werden 10.000 Artikel an verschiedene Lager verschickt.
Ermittle die erwartete Anzahl der fehlerhaften Artikel, die Varianz und die Standardabweichung.
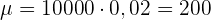
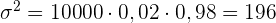
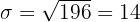
Wahrscheinlichkeit beim Ziehen von Kugeln aus einer Urne
In einer Urne befinden sich insgesamt 30 Kugeln: 10 rote, 20 weiße Kugeln.
Eine Kugel wird nach dem Zufallsprinzip gezogen und es wird notiert, ob sie rot ist; der Vorgang wird 10 Mal wiederholt, wobei die gezogene Kugel immer zurückgelegt wird.
Berechne den Mittelwert und die Standardabweichung.
In einer Urne befinden sich insgesamt 30 Kugeln: 10 rote, 20 weiße Kugeln.
Eine Kugel wird nach dem Zufallsprinzip gezogen und es wird notiert, ob sie rot ist; der Vorgang wird 10 Mal wiederholt, wobei die gezogene Kugel immer zurückgelegt wird. Berechne den Mittelwert und die Standardabweichung.
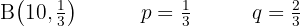
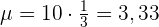
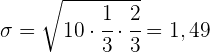
Arzneimittelexperiment: Wahrscheinlichkeit von Nebenwirkungen
Ein Labor gibt an, dass ein Medikament bei 3 von 100 Patienten Nebenwirkungen verursacht.
Um diese Behauptung zu überprüfen, wählt ein anderes Labor nach dem Zufallsprinzip 5 Patienten aus, denen es das Medikament verabreicht.
Wie hoch ist die Wahrscheinlichkeit der folgenden Ereignisse?
1 Nebenwirkungen bei keinem der Patienten
2 Nebenwirkungen bei mindestens 2 Patienten
3 Bei wie vielen Patienten erwartet das Labor im Durchschnitt Nebenwirkungen, wenn 100 Patienten zufällig ausgewählt werden?
Ein Labor gibt an, dass ein Medikament bei 3 von 100 Patienten Nebenwirkungen verursacht. Um diese Behauptung zu überprüfen, wählt ein anderes Labor nach dem Zufallsprinzip 5 Patienten aus, denen es das Medikament verabreicht.
Wie hoch ist die Wahrscheinlichkeit der folgenden Ereignisse?
1 Nebenwirkungen bei keinem der Patienten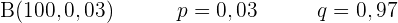
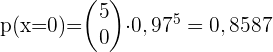
2 Nebenwirkungen bei mindestens 2 Patienten
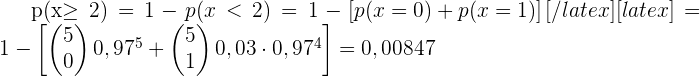
3 Bei wie vielen Patienten erwartet das Labor im Durchschnitt Nebenwirkungen, wenn 100 Patienten zufällig ausgewählt werden?
Mit KI zusammenfassen:



