In diesem Artikel haben wir mehrere Aufgaben, bei denen das Integral eine Rolle spielt, auch wenn wir direkt aufgefordert werden, eine Funktion zu „integrieren“. In den meisten Fällen wird der Begriff „Stammfunktion“ erwähnt. Falls du dir über diesen Begriff nicht im Klaren bist, laden wir dich ein, unsere diesbezüglichen Artikel zu lesen. Ebenso wird in den ersten Übungen kurz erwähnt, was eine Stammfunktion ist.
Welche der unendlich vielen Stammfunktionen der Funktion  hat den Wert
hat den Wert  , wenn sie für
, wenn sie für  ausgewertet wird?
ausgewertet wird?
Zunächst sei daran erinnert, dass die Stammfunktion einer Funktion  eine Funktion
eine Funktion  ist, die die Bedingung
ist, die die Bedingung 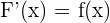 erfüllt. Nun wollen wir die allgemeine Form der Stammfunktion der Funktion
erfüllt. Nun wollen wir die allgemeine Form der Stammfunktion der Funktion  ermitteln. Die Stammfunktionen werden durch unbestimmte Integrale berechnet:
ermitteln. Die Stammfunktionen werden durch unbestimmte Integrale berechnet:
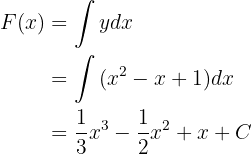
Daher haben wir 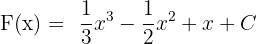 . Wir sollen jedoch die Stammfunktion finden, die erfüllt, dass
. Wir sollen jedoch die Stammfunktion finden, die erfüllt, dass  ist. Wir tun dies, indem wir die allgemeine Stammfunktion auswerten und den genauen Wert von
ist. Wir tun dies, indem wir die allgemeine Stammfunktion auswerten und den genauen Wert von  finden, der diese Gleichheit gewährleistet. Somit
finden, der diese Gleichheit gewährleistet. Somit
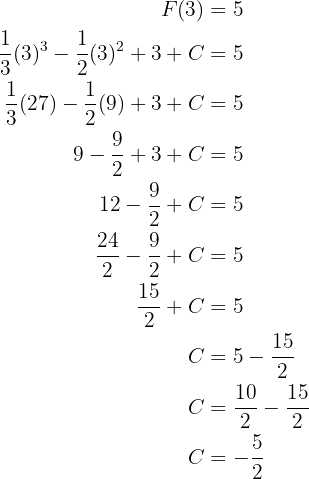
Wir haben unseren Wert für 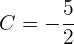 gefunden, die gesuchte Stammfunktion ist also
gefunden, die gesuchte Stammfunktion ist also
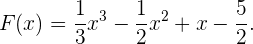
Ermittle die Stammfunktion der Funktion  , die durch den Punkt
, die durch den Punkt  verläuft.
verläuft.
Die allgemeine Form der Stammfunktionen erhalten wir durch das Integral mit unbestimmten Grenzwerten, d. h.
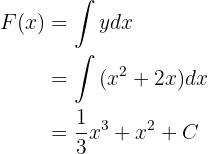
Wir haben also 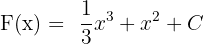 . Es geht jedoch darum, die Stammfunktion zu finden, die durch den Punkt
. Es geht jedoch darum, die Stammfunktion zu finden, die durch den Punkt  verläuft, d. h., dass
verläuft, d. h., dass  . Wir tun dies, indem wir die allgemeine Stammfunktion auswerten und den genauen Wert von
. Wir tun dies, indem wir die allgemeine Stammfunktion auswerten und den genauen Wert von  finden, der diese Gleichheit gewährleistet. Somit
finden, der diese Gleichheit gewährleistet. Somit
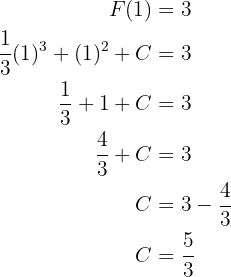
Wir haben unseren Wert für 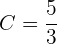 gefunden, also lautet die gesuchte Stammfunktion
gefunden, also lautet die gesuchte Stammfunktion
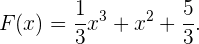
Finde eine Funktion  , die für
, die für  den Wert
den Wert  annimmt und deren Ableitung
annimmt und deren Ableitung 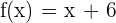 ist.
ist.
Die Aufgabe sagt uns, dass  eine Stammfunktion von
eine Stammfunktion von  ist. Um
ist. Um  zu finden, müssen wir also zunächst die Stammfunktionen von
zu finden, müssen wir also zunächst die Stammfunktionen von  ermitteln, was wir durch Integration tun
ermitteln, was wir durch Integration tun
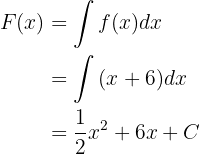
Nun muss  erfüllen, dass
erfüllen, dass 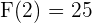 . Wir werten aus und stellen fest, dass
. Wir werten aus und stellen fest, dass  diese Gleichheit erfüllt
diese Gleichheit erfüllt
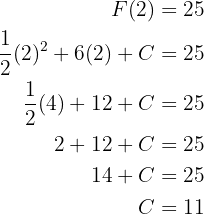
Unsere gesuchte Funktion ist also
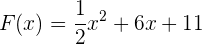
Finde eine Gerade, deren Steigung  ist und die durch den Punkt
ist und die durch den Punkt  verläuft.
verläuft.
Obwohl dieses Problem direkt mit der allgemeinen Formel für die Gerade gelöst werden kann, werden wir hier das Integral anwenden. Erstens ist die Ableitung einer Geraden ihre Steigung. Sie ist konstant, d. h. wenn wir also folgende Gerade haben,
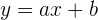
Ihre Ableitung ist ihre Steigung  . Da die Steigung der Geraden
. Da die Steigung der Geraden  ist, d. h. ihre Ableitung
ist, d. h. ihre Ableitung  , müssen wir die Stammfunktionen dieser Konstante ermitteln
, müssen wir die Stammfunktionen dieser Konstante ermitteln
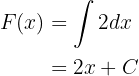
dann haben alle Geraden mit der Steigung  die Form
die Form 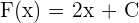 ; diese Gerade muss aber durch den Punkt
; diese Gerade muss aber durch den Punkt 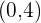 verlaufen, also
verlaufen, also
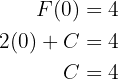
Die gesuchte Gerade ist also gegeben durch

Ermittle die Stammfunktion der Funktion
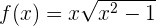 ,
,
die für  null wird.
null wird.
Um dieses Problem zu lösen, müssen wir zunächst die Stammfunktionen von  finden. Wir ermitteln die Stammfunktionen durch das Integral und integrieren nach der Substitutionsmethode. Wir nehmen
finden. Wir ermitteln die Stammfunktionen durch das Integral und integrieren nach der Substitutionsmethode. Wir nehmen
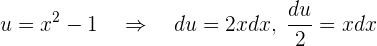
Wir substituieren und erhalten
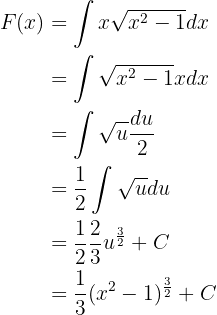
Nun stellen wir fest, dass der Graph für  0 wird. , Das bedeutet, dass er bei
0 wird. , Das bedeutet, dass er bei  den Wert
den Wert  annimmt. Somit ist
annimmt. Somit ist 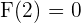 und wir können den Wert für
und wir können den Wert für  ermitteln
ermitteln
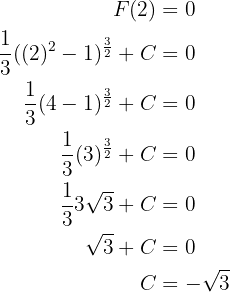
Somit ist unser Graph
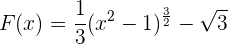
Mit KI zusammenfassen:


