Aufgaben
Stelle die Gerade dar: 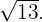
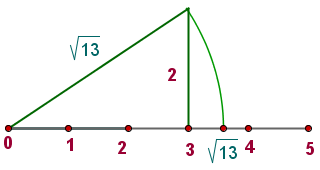
Wir nehmen ein Rechteck mit der Basis 3 und der Seite 2. Nach dem Satz des Pythagoras wissen wir dann, dass die Diagonale  ist. In der Tat bedeutet dies, dass
ist. In der Tat bedeutet dies, dass 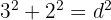 , wobei
, wobei 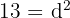 und somit
und somit 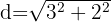 . Man nimmt einfach dieses Maß und transponiert es mit dem Zirkel (wobei der Mittelpunkt bei
. Man nimmt einfach dieses Maß und transponiert es mit dem Zirkel (wobei der Mittelpunkt bei  liegt und der Radius die Diagonale unseres Rechtecks ist). Wir stellen also auf der Zahlengeraden die Zahl
liegt und der Radius die Diagonale unseres Rechtecks ist). Wir stellen also auf der Zahlengeraden die Zahl  dar.
dar.
Stelle auf der Zahlengeraden die Zahlen dar, die die folgenden Beziehungen erfüllen:
1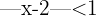
2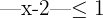
3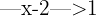
4 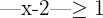
Für jeden dieser Fälle lösen wir den Betrag und zeichnen dann das Segment, das er darstellt:
1 Zunächst verwenden wir die Definition des Betrags, dann addieren wir  zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall:
zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall: 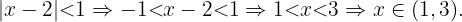

2 Zunächst verwenden wir die Definition des Betrags, dann addieren wir  zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall:
zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall: 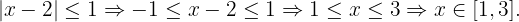

3 Zunächst verwenden wir die Definition des Betrags, dann addieren wir  zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall:
zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall: 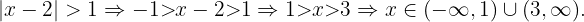

4 Zunächst verwenden wir die Definition des Betrags, dann addieren wir  zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall:
zu den beiden Ungleichungen. Schließlich erhalten wir das gesuchte Intervall: 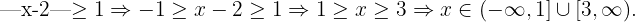

Berechne: 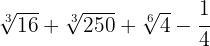
Wir zerlegen die Radikanden in Faktoren:  Bei den ersten beiden Summanden extrahieren wir Faktoren, beim dritten vereinfachen wir die Wurzel, indem wir den Wurzelexponenten und den Exponenten des Radikanden durch
Bei den ersten beiden Summanden extrahieren wir Faktoren, beim dritten vereinfachen wir die Wurzel, indem wir den Wurzelexponenten und den Exponenten des Radikanden durch  dividieren, und den letzten rationalisieren wir, indem wir mit der Kubikwurzel von
dividieren, und den letzten rationalisieren wir, indem wir mit der Kubikwurzel von  multiplizieren und dividieren
multiplizieren und dividieren

Da alle Wurzeln gleich sind, können wir ihre Koeffizienten addieren
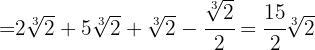
Berechne: 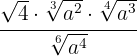
Zunächst berechnen wir das kleinste gemeinsame Vielfache der Wurzelexponenten. Dies ist dann unser gemeinsamer Wurzelexponent
Wir dividieren den gemeinsamen Wurzelexponenten  durch die einzelnen Wurzelexponenten
durch die einzelnen Wurzelexponenten 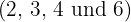 und jedes erhaltene Ergebnis multiplizieren wir mit den entsprechenden Exponenten
und jedes erhaltene Ergebnis multiplizieren wir mit den entsprechenden Exponenten 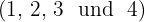
Wir entfernen die Klammern, vereinfachen den Bruch und multiplizieren im Zähler die Potenzen mit der gleichen Basis
Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und den Exponenten der Wurzel durch  dividieren
dividieren
Schließlich berechnen wir
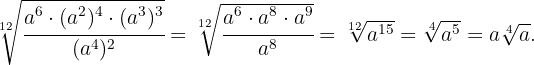
Rationalisiere: 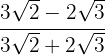
Wir multiplizieren Zähler und Nenner mit dem konjugierten Wert des Nenners
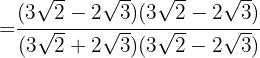
Wir schreiben den Zähler als Potenz
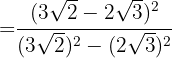
Im Zähler haben wir eine quadrierte Differenz, die gleich dem Quadrat des ersten, minus dem Doppelten des ersten mal dem zweiten, plus dem Quadrat des zweiten ist
Wir berechnen wie folgt

Und
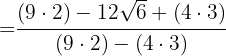

Wir vereinfachen den Bruch
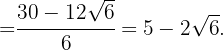
Gegeben ist 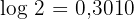 . Berechne:
. Berechne: 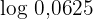
Zunächst schreiben wir die Zahl 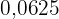 als Bruch , und zerlegen diesen Bruch in Potenzen von Primzahlen. Schließlich wenden wir die Eigenschaft des Logarithmus einer Division an:
als Bruch , und zerlegen diesen Bruch in Potenzen von Primzahlen. Schließlich wenden wir die Eigenschaft des Logarithmus einer Division an: 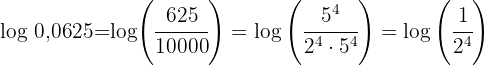
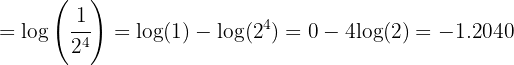
Berechne den Wert von  unter Anwendung der Definition des Logarithmus:
unter Anwendung der Definition des Logarithmus:
1 
2 
3 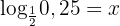
4 
5 
6 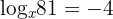
7 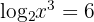
In jeder der Aufgaben führen wir die notwendigen Berechnungen durch, um den Wert von  zu erhalten.
zu erhalten.

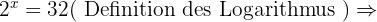
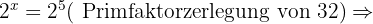


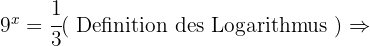
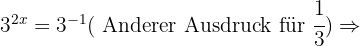
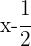
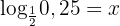
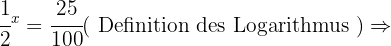
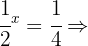
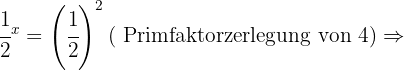


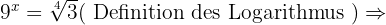
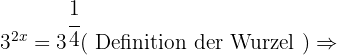
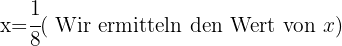

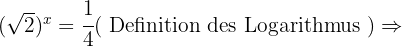
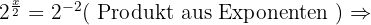
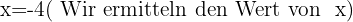
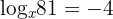
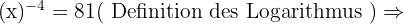
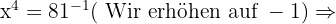
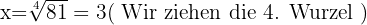
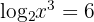
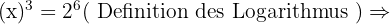
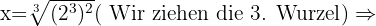
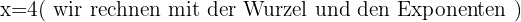
Gegeben ist 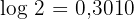 . Berechne die folgenden dezimalen Logarithmen.
. Berechne die folgenden dezimalen Logarithmen.
1 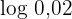
2 
3 
Wir führen die jeweiligen Berechnungen durch, um den gesuchten Wert zu ermitteln
 als Bruch und wenden im Anschluss die Eigenschaften des Logarithmus einer Division und einer Potenz an
als Bruch und wenden im Anschluss die Eigenschaften des Logarithmus einer Division und einer Potenz an 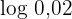
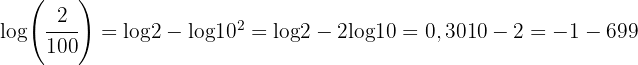
 als Potenz und wenden die Eigenschaft des Logarithmus einer Potenz an
als Potenz und wenden die Eigenschaft des Logarithmus einer Potenz an 
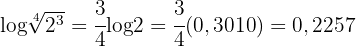
 als Bruch und wenden die Eigenschaft des Logarithmus einer Division an
als Bruch und wenden die Eigenschaft des Logarithmus einer Division an 
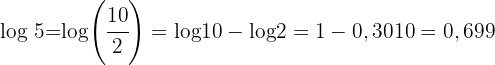
Berechne die Logarithmen der angegebenen Ausdrücke:
1 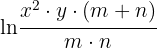
2 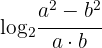
3 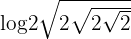
Wir führen die jeweiligen Berechnungen durch, um den gesuchten Wert zu ermitteln


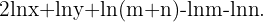
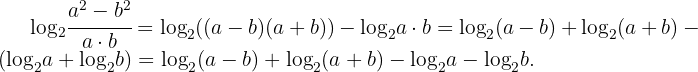
 , Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz
, Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz  , Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz
, Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz  , Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz
, Logarithmus eines Produkts, Logarithmus einer Potenz mit Potenz  :
: 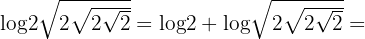


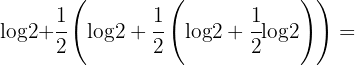
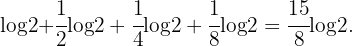
Berechne mithilfe von Logarithmen den Wert von  .
.
1 
2 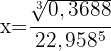
3 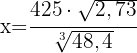
Wir führen die jeweiligen Berechnungen durch, um den gesuchten Wert zu ermitteln
 Wir wenden auf beiden Seiten den Logarithmus an
Wir wenden auf beiden Seiten den Logarithmus an 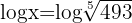 Wir wenden den Logarithmus einer Potzenz an
Wir wenden den Logarithmus einer Potzenz an 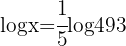 Wir bestimmen den Gegenalgorithmus
Wir bestimmen den Gegenalgorithmus 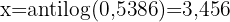
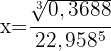 Wir wenden auf beiden Seiten den Logarithmus an
Wir wenden auf beiden Seiten den Logarithmus an 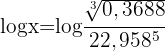 Wir wenden den Logarithmus einer Division an
Wir wenden den Logarithmus einer Division an 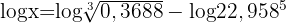
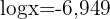 Wir wenden den Gegenlogarithmus an
Wir wenden den Gegenlogarithmus an 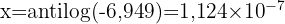
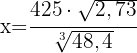 Wir wenden auf beiden Seiten den Logarithmus an
Wir wenden auf beiden Seiten den Logarithmus an 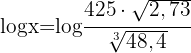 Wir wenden den Logarithmus einer Division, den Logarithmus eines Produkts und den Logarithmus einer Potenz an
Wir wenden den Logarithmus einer Division, den Logarithmus eines Produkts und den Logarithmus einer Potenz an 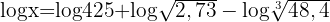
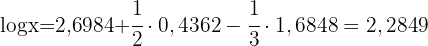 Wir wenden auf beiden Seiten den Logarithmus an
Wir wenden auf beiden Seiten den Logarithmus an 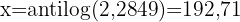
Mit KI zusammenfassen:


