Das vierte Glied einer arithmetischen Folge ist  und das sechste Glied ist
und das sechste Glied ist  . Schreibe die arithmetische Folge.
. Schreibe die arithmetische Folge.
Das vierte Glied einer arithmetischen Folge ist  und das sechste Glied ist
und das sechste Glied ist  . Schreibe die arithmetische Folge.
. Schreibe die arithmetische Folge.
1 Folgende Werte der Folge sind bekannt:
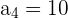 und
und 
2 Eine arithmetische Folge hat den Ausdruck:
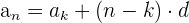
3 Wir setzen die Werte ein und erhalten die Differenz " " zwischen den Gliedern der Folge:
" zwischen den Gliedern der Folge:
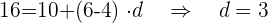
4 Wir erhalten den Wert des ersten Glieds der Folge:
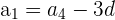

5 Die arithmetische Folge ist:
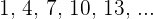
Ermittle drei arithmetische Mittel zwischen  und
und  .
.
Ermittle drei arithmetische Mittel zwischen  und
und  .
.
1 Folgende Werte sind bekannt:
 und
und 
2 Die Differenz zwischen den Gliedern der Folge erhalten wir mit der Formel:
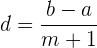
3 Wir setzen ein und lösen:

4 Die Folge ist:

Ermittle drei arithmetische Mittel zwischen  und
und  .
.
Ermittle drei arithmetische Mittel zwischen  und
und 
1 Folgende Werte der Folge sind bekannt:
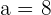 und
und 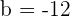
2 Die Differenz zwischen den Gliedern der Folge erhalten wir mit der Formel:
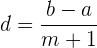
3 Wir setzen ein und lösen:

4 Die Folge ist:
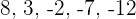
Das erste Glied einer arithmetischen Folge ist  und das 15. Glied ist
und das 15. Glied ist  . Ermittle die Differenz und die Summe der 15 ersten Glieder.
. Ermittle die Differenz und die Summe der 15 ersten Glieder.
Das erste Glied einer arithmetischen Folge ist  und das 15. Glied ist
und das 15. Glied ist  . Ermittle die Differenz und die Summe der 15 ersten Glieder.
. Ermittle die Differenz und die Summe der 15 ersten Glieder.
1 Folgende Werte sind bekannt:
 und
und 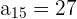
2 Bei einer arithmetischen Folge gilt:
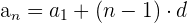
3 Wir setzen die Werte ein:
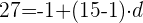
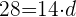
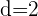
4 Die Differenz ist 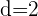
5 Um die Summe der ersten  Glieder zu berechnen, wenden wir folgende Formel an:
Glieder zu berechnen, wenden wir folgende Formel an:
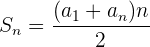
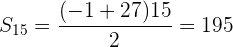
Ermittle die Summe der ersten 15 Vielfachen von  .
.
Ermittle die Summe der ersten 15 Vielfachen von 
1 Folgende Werte sind bekannt:
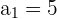 ,
, 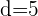 und
und 
2 Bei einer arithmetischen Folge gilt:
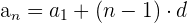
3 Wir setzen ein und erhalten so das 15. Glied:

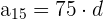
4 Um die Summe der ersten  Glieder zu berechnen, wenden wir folgende Formel an:
Glieder zu berechnen, wenden wir folgende Formel an:
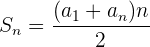

Ermittle die Summe der 15 ersten Zahlen, die auf  enden.
enden.
Ermittle die Summe der ersten 15 Zahlen, die auf  enden.
enden.
1 Folgende Werte sind bekannt:
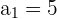 ,
, 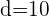 und
und 
2 Bei einer arithmetischen Folge gilt:
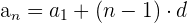
3 Wir setzen die Werte ein und erhalten so das 15. Glied:

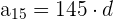
4 Um die Summe der ersten  Glieder zu berechnen, wenden wir folgende Formel an:
Glieder zu berechnen, wenden wir folgende Formel an:
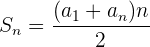

Ermittle die Summe der 15 ersten geraden Zahlen, die größer als  sind.
sind.
Ermittle die Summe der 15 ersten geraden Zahlen, die größer als  sind.
sind.
1 Folgende Werte sind bekannt:
 ,
, 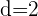 und
und 
2 Bei einer arithmetischen Folge gilt:
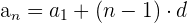
3 Wir setzen die Werte ein und erhalten so das 15. Glied:
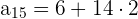
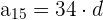
4 Um die Summe der ersten  Glieder zu erhalten, nutzen wir folgende Formel:
Glieder zu erhalten, nutzen wir folgende Formel:
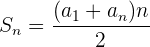
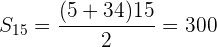
Bestimme die Winkel eines konvexen Vierecks, wenn bekannt ist, dass sie einer arithmetischen Folge unterliegen und 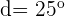 ist.
ist.
Bestimme die Winkel eines konvexen Vierecks, wenn bekannt ist, dass sie einer arithmetischen Folge unterliegen und 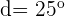 ist.
ist.
1 Wir wissen, dass die Summe der Innenwinkel eines Vierecks  ist. Deshalb setzen wir in die Formel der Summe die ersten Glieder ein und erhalten:
ist. Deshalb setzen wir in die Formel der Summe die ersten Glieder ein und erhalten:
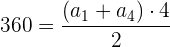
2 Außerdem wissen wir, dass zwischen dem ersten und vierten Glied folgende Beziehung besteht:

3 Wir setzen den zweiten Ausdruck in den ersten ein und erhalten:

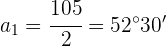
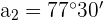
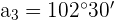

Die kürzere Kathete eines rechtwinkligen Dreiecks misst  cm.
cm.
Berechne die anderen beiden Seiten, wobei bekannt ist, dass die Seiten des Dreiecks eine arithmetische Folge bilden.
Die kürzere Kathete eines rechtwinkligen Dreiecks misst  cm.
cm.
1 Berechne die anderen beiden Seiten, wobei bekannt ist, dass die Seiten des Dreiecks eine arithmetische Folge bilden.


2 Wir wenden den Satz des Pythagoras an
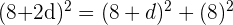
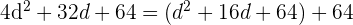

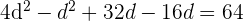
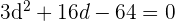
3 Wir lösen mit der allgemeinen Formel für quadratische Gleichungen:
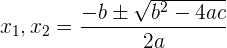
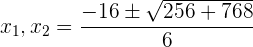
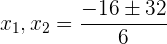

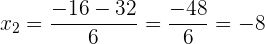
4 Da das Ergebnis nicht negativ sein kann, erhalten wir:
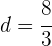
5 Die negative Lösung ist nicht gültig, da die Länge der Seiten eines Dreiecks positiv sein muss

Berechne drei Zahlen einer arithmetischen Folge, deren Summe  ist. Die Summe der Zahlen zum Quadrat ist
ist. Die Summe der Zahlen zum Quadrat ist 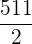 .
.
Berechne drei Zahlen einer arithmetischen Folge, deren Summe  ist. Die Summe der Zahlen zum Quadrat ist
ist. Die Summe der Zahlen zum Quadrat ist 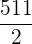 .
.
1 Wir benennen das zentrale Glied mit 
2 Das erste Glied ist somit: 
3 Das dritte Glied ist somit: 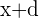
4 Die Summe der drei Glieder ist  , somit:
, somit:


5 Die Summe der  Zahlen zum Quadrat ist
Zahlen zum Quadrat ist 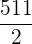 . Somit:
. Somit:


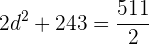
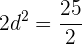

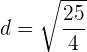
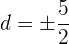
6 Wir haben zwei Folgen, die die Bedingung erfüllen (eine für den positiven Wert für ' ' und die andere für den negativen Wert)
' und die andere für den negativen Wert)
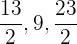

Mit KI zusammenfassen:



