Kapitel

Tabelle der Normalverteilung
Die Tabelle der Normalverteilung wird verwendet, um definierte Werte für die Variable z zu finden.
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
| -3.4 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0003 | .0002 |
| -3.3 | .0005 | .0005 | .0005 | .0004 | .0004 | .0004 | .0004 | .0004 | .0004 | .0003 |
| -3.2 | .0007 | .0007 | .0006 | .0006 | .0006 | .0005 | .0005 | .0005 | .0004 | .0004 |
| -3.1 | .0010 | .0009 | .0009 | .0009 | .0008 | .0008 | .0008 | .0007 | .0007 | .0006 |
| -3.0 | .0013 | .0013 | .0012 | .0012 | .0011 | .0011 | .0010 | .0010 | .0009 | .0009 |
| -2.9 | .0019 | .0018 | .0018 | .0017 | .0016 | .0016 | .0015 | .0015 | .0014 | .0014 |
| -2.8 | .0026 | .0025 | .0024 | .0023 | .0022 | .0021 | .0021 | .0020 | .0019 | .0018 |
| -2.7 | .0035 | .0034 | .0033 | .0032 | .0031 | .0030 | .0029 | .0028 | .0027 | .0026 |
| -2.6 | .0047 | .0045 | .0044 | .0043 | .0041 | .0040 | .0039 | .0038 | .0037 | .0036 |
| -2.5 | .0062 | .0060 | .0059 | .0057 | .0055 | .0054 | .0052 | .0051 | .0049 | .0048 |
| -2.4 | .0082 | .0080 | .0078 | .0075 | .0073 | .0071 | .0069 | .0068 | .0066 | .0064 |
| -2.3 | .0107 | .0104 | .0102 | .0099 | .0097 | .0094 | .0091 | .0089 | .0087 | .0084 |
| -2.2 | .0139 | .0136 | .0132 | .0129 | .0125 | .0122 | .0119 | .0116 | .0113 | .0110 |
| -2.1 | .0179 | .0174 | .0170 | .0166 | .0162 | .0158 | .0154 | .0150 | .0146 | .0143 |
| -2.0 | .0228 | .0222 | .0217 | .0212 | .0207 | .0202 | .0197 | .0192 | .0188 | .0183 |
| -1.9 | .0287 | .0281 | .0274 | .0268 | .0262 | .0256 | .0250 | .0244 | .0239 | .0233 |
| -1.8 | .0359 | .0351 | .0344 | .0336 | .0329 | .0322 | .0314 | .0307 | .0301 | .0294 |
| -1.7 | .0446 | .0436 | .0427 | .0418 | .0409 | .0401 | .0392 | .0384 | .0375 | .0367 |
| -1.6 | .0548 | .0537 | .0526 | .0516 | .0505 | .0495 | .0485 | .0475 | .0465 | .0455 |
| -1.5 | .0668 | .0655 | .0643 | .0630 | .0618 | .0606 | .0594 | .0582 | .0571 | .0559 |
| -1.4 | .0808 | .0793 | .0778 | .0764 | .0749 | .0735 | .0721 | .0708 | .0694 | .0681 |
| -1.3 | .0968 | .0951 | .0934 | .0918 | .0901 | .0885 | .0869 | .0853 | .0838 | .0823 |
| -1.2 | .1151 | .1131 | .1112 | .1093 | .1075 | .1056 | .1038 | .1020 | .1003 | .0985 |
| -1.1 | .1357 | .1335 | .1314 | .1292 | .1271 | .1251 | .1230 | .1210 | .1190 | .1170 |
| -1.0 | .1587 | .1562 | .1539 | .1515 | .1492 | .1469 | .1446 | .1423 | .1401 | .1379 |
| -0.9 | .1841 | .1814 | .1788 | .1762 | .1736 | .1711 | .1685 | .1660 | .1635 | .1611 |
| -0.8 | .2119 | .2090 | .2061 | .2033 | .2005 | .1977 | .1949 | .1922 | .1894 | .1867 |
| -0.7 | .2420 | .2389 | .2358 | .2327 | .2296 | .2266 | .2236 | .2206 | .2177 | .2148 |
| -0.6 | .2743 | .2709 | .2676 | .2643 | .2611 | .2578 | .2546 | .2514 | .2483 | .2451 |
| -0.5 | .3085 | .3050 | .3015 | .2981 | .2946 | .2912 | .2877 | .2843 | .2810 | .2776 |
| -0.4 | .3446 | .3409 | .3372 | .3336 | .3300 | .3264 | .3228 | .3192 | .3156 | .3121 |
| -0.3 | .3821 | .3783 | .3745 | .3707 | .3669 | .3632 | .3594 | .3557 | .3520 | .3483 |
| -0.2 | .4207 | .4168 | .4129 | .4090 | .4052 | .4013 | .3974 | .3936 | .3897 | .3859 |
| -0.1 | .4602 | .4562 | .4522 | .4483 | .4443 | .4404 | .4364 | .4325 | .4286 | .4247 |
| 0.0 | .5000 | .4960 | .4920 | .4880 | .4840 | .4801 | .4761 | .4721 | .4681 | .4641 |
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | .5000 | .5040 | .5080 | .5120 | .5160 | .5199 | .5239 | .5279 | .5319 | .5359 |
| 0.1 | .5398 | .5438 | .5478 | .5517 | .5557 | .5596 | .5636 | .5675 | .5714 | .5753 |
| 0.2 | .5793 | .5832 | .5871 | .5910 | .5948 | .5987 | .6026 | .6064 | .6103 | .6141 |
| 0.3 | .6179 | .6217 | .6255 | .6293 | .6331 | .6368 | .6406 | .6443 | .6480 | .6517 |
| 0.4 | .6554 | .6591 | .6628 | .6664 | .6700 | .6736 | .6772 | .6808 | .6844 | .6879 |
| 0.5 | .6915 | .6950 | .6985 | .7019 | .7054 | .7088 | .7123 | .7157 | .7190 | .7224 |
| 0.6 | .7257 | .7291 | .7324 | .7357 | .7389 | .7422 | .7454 | .7486 | .7517 | .7549 |
| 0.7 | .7580 | .7611 | .7642 | .7673 | .7704 | .7734 | .7764 | .7794 | .7823 | .7852 |
| 0.8 | .7881 | .7910 | .7939 | .7967 | .7995 | .8023 | .8051 | .8078 | .8106 | .8133 |
| 0.9 | .8159 | .8186 | .8212 | .8238 | .8264 | .8289 | .8315 | .8340 | .8365 | .8389 |
| 1.0 | .8413 | .8438 | .8461 | .8485 | .8508 | .8531 | .8554 | .8577 | .8599 | .8621 |
| 1.1 | .8643 | .8665 | .8686 | .8708 | .8729 | .8749 | .8770 | .8790 | .8810 | .8830 |
| 1.2 | .8849 | .8869 | .8888 | .8907 | .8925 | .8944 | .8962 | .8980 | .8997 | .9015 |
| 1.3 | .9032 | .9049 | .9066 | .9082 | .9099 | .9115 | .9131 | .9147 | .9162 | .9177 |
| 1.4 | .9192 | .9207 | .9222 | .9236 | .9251 | .9265 | .9279 | .9292 | .9306 | .9319 |
| 1.5 | .9332 | .9345 | .9357 | .9370 | .9382 | .9394 | .9406 | .9418 | .9429 | .9441 |
| 1.6 | .9452 | .9463 | .9474 | .9484 | .9495 | .9505 | .9515 | .9525 | .9535 | .9545 |
| 1.7 | .9554 | .9564 | .9573 | .9582 | .9591 | .9599 | .9608 | .9616 | .9625 | .9633 |
| 1.8 | .9641 | .9649 | .9656 | .9664 | .9671 | .9678 | .9686 | .9693 | .9699 | .9706 |
| 1.9 | .9713 | .9719 | .9726 | .9732 | .9738 | .9744 | .9750 | .9756 | .9761 | .9767 |
| 2.0 | .9772 | .9778 | .9783 | .9788 | .9793 | .9798 | .9803 | .9808 | .9812 | .9817 |
| 2.1 | .9821 | .9826 | .9830 | .9834 | .9838 | .9842 | .9846 | .9850 | .9854 | .9857 |
| 2.2 | .9861 | .9864 | .9868 | .9871 | .9875 | .9878 | .9881 | .9884 | .9887 | .9890 |
| 2.3 | .9893 | .9896 | .9898 | .9901 | .9904 | .9906 | .9909 | .9911 | .9913 | .9916 |
| 2.4 | .9918 | .9920 | .9922 | .9925 | .9927 | .9929 | .9931 | .9932 | .9934 | .9936 |
| 2.5 | .9938 | .9940 | .9941 | .9943 | .9945 | .9946 | .9948 | .9949 | .9951 | .9952 |
| 2.6 | .9953 | .9955 | .9956 | .9957 | .9959 | .9960 | .9961 | .9962 | .9963 | .9964 |
| 2.7 | .9965 | .9966 | .9967 | .9968 | .9969 | .9970 | .9971 | .9972 | .9973 | .9974 |
| 2.8 | .9974 | .9975 | .9976 | .9977 | .9977 | .9978 | .9979 | .9979 | .9980 | .9981 |
| 2.9 | .9981 | .9982 | .9982 | .9983 | .9984 | .9984 | .9985 | .9985 | .9986 | .9986 |
| 3.0 | .9987 | .9987 | .9987 | .9988 | .9988 | .9989 | .9989 | .9989 | .9990 | .9990 |
| 3.1 | .9990 | .9991 | .9991 | .9991 | .9992 | .9992 | .9992 | .9992 | .9993 | .9993 |
| 3.2 | .9993 | .9993 | .9993 | .9994 | .9994 | .9994 | .9994 | .9994 | .9994 | .9995 |
| 3.3 | .9995 | .9995 | .9995 | .9995 | .9995 | .9995 | .9995 | .9996 | .9996 | .9996 |
| 3.4 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9998 |
Zufallsvariablen der Normalverteilung
Wenn  eine Zufallsvariable einer Normalverteilung
eine Zufallsvariable einer Normalverteilung 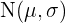 ist, bestimme:
ist, bestimme:  .
.
In diesem Fall arbeiten wir mit einer Standardnormalverteilung, für deren Lösung wir die folgende Formel verwenden werden:
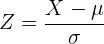
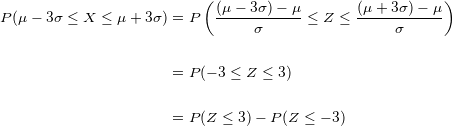
Nun müssen wir in unserer Normalverteilungstabelle den Wert suchen, bei dem 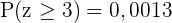 ist. Wir benötigen allerdings den Wert, bei dem
ist. Wir benötigen allerdings den Wert, bei dem 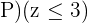 und rechnen also
und rechnen also 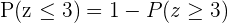 . So erhalten wir
. So erhalten wir 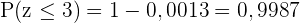 . Da die Normalverteilung außerdem symmetrisch ist, gilt:
. Da die Normalverteilung außerdem symmetrisch ist, gilt: 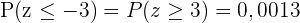 .
.
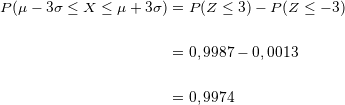
Die Wahrscheinlichkeit liegt somit bei 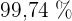 der Werte für
der Werte für  .
.
Normalverteilung, Mittelwert und Standardabweichung:
Gegeben ist eine Normalverteilung mit dem Mittelwert  und der Standardabweichung
und der Standardabweichung  . Berechne den Wert für a, sodass:
. Berechne den Wert für a, sodass: 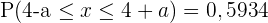
Wir wenden die Formel 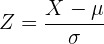 an und setzen den Wert des Mittelwerts (
an und setzen den Wert des Mittelwerts (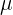 ) und die Standardabweichung (
) und die Standardabweichung ( 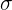 ) ein.
) ein.
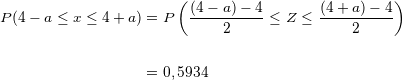
Wir vereinfachen und erhalten:
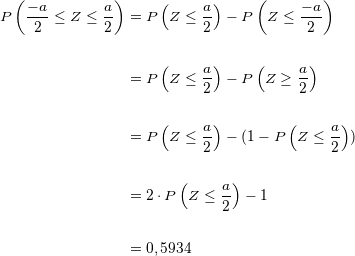
Hieraus ergibt sich

Nun suchen wir in der Normalverteilungstabelle den Wert 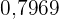 und sehen, dass er
und sehen, dass er 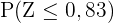 entspricht. Somit:
entspricht. Somit:
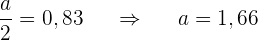
Die Normalverteilung in Anwendung auf die Umgebungstemperatur
Es wird geschätzt, dass die Höchsttemperatur in einer Stadt im Juni einer Normalverteilung folgt, mit einem Mittelwert von 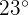 und einer Standardabweichung von
und einer Standardabweichung von 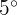 .
.
Berechne die Anzahl der Tage des Monats, an denen Temperaturen zwischen 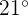 und
und 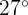 zu erwarten sind.
zu erwarten sind.
Wir wenden die Formel 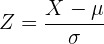 an und setzen den Wert des Mittelwerts (
an und setzen den Wert des Mittelwerts ( ) und die Standardabweichung (
) und die Standardabweichung (  ) ein.
) ein.
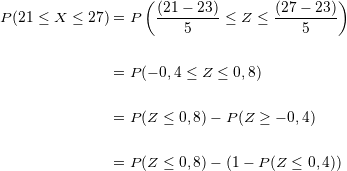
Wir suchen die entsprechenden Werte in der Normalverteilungstabelle:
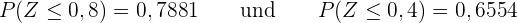
Deshalb gilt
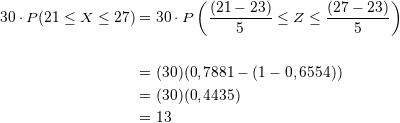
Das bedeutet, dass im Juni nur an  Tagen Temperaturen zwischen
Tagen Temperaturen zwischen  Grad und
Grad und  Grad erreicht werden.
Grad erreicht werden.
Die Normalverteilung in Anwendung auf das Gewicht von Schüler*innen
Der Mittelwert des Gewichts von  Schüler*innen einer Schule liegt bei
Schüler*innen einer Schule liegt bei 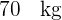 und die Standardabweichung bei
und die Standardabweichung bei 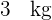 .
.
Es gilt die Annahme, dass das Gewicht normal verteilt ist. Ermittle, wieviele Schüler*innen folgendes Gewicht haben:
1 Zwischen 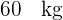 und
und  .
.
2 Mehr als  .
.
3 Weniger als  .
.
4  .
.
5  oder weniger.
oder weniger.
1
Wir setzen ein:
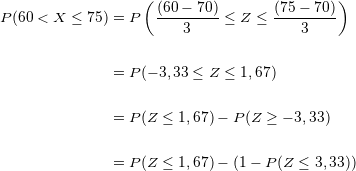
Wir suchen die Werte in der Normalverteilungstabelle:
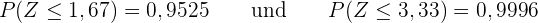
Wenn wir also die Wahrscheinlichkeit 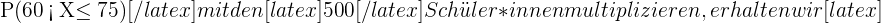
Von den  Schüler*innen wiegen
Schüler*innen wiegen  zwischen
zwischen  und
und  kg.
kg.
2
Wir setzen ein und vereinfachen:
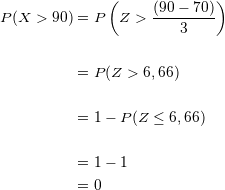
Wir multiplizieren die Wahrscheinlichkeit mit  und erhalten
und erhalten
 .
.
Es wiegt also kein*e Schüler*in mehr als  kg.
kg.
3
Wir setzen ein und vereinfachen:
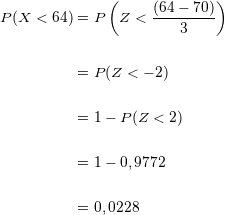
Wir multiplizieren die Wahrscheinlichkeit mit  und erhalten
und erhalten
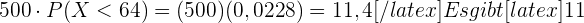 Schüler*innen, die weniger als
Schüler*innen, die weniger als  kg wiegen.
kg wiegen.
4
Bei einer stetigen Verteilung ist die Wahrscheinlichkeit, dass die Variable einen exakten Wert hat, immer null ( ). Somit gilt
). Somit gilt
 .
.
5
Angesichts der oben genannten Ergebnisse:
Es gibt null Schüler*innen, die genau  kg wiegen und
kg wiegen und  Schüler*innen, die weniger als
Schüler*innen, die weniger als  kg wiegen. Somit gibt es
kg wiegen. Somit gibt es  Schüler*innen, die
Schüler*innen, die  kg oder weniger wiegen.
kg oder weniger wiegen.
 \displaystyle 500 \cdot P(X < 64) = 500 \cdot P(X \leq 64) = 11[/latex].
\displaystyle 500 \cdot P(X < 64) = 500 \cdot P(X \leq 64) = 11[/latex].
Die Normalverteilung in Anwendung auf Prüfungsergebnisse
Es wird angenommen, dass die Ergebnisse einer Prüfung einer Normalverteilung mit einem Mittelwert von 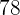 und einer Standardabweichung von
und einer Standardabweichung von  folgen.
folgen.
1 Wie hoch ist die Wahrscheinlichkeit, dass eine Person, die an der Prüfung teilnimmt, eine höhere Punktzahl als  erreicht?
erreicht?
2 Berechne den Anteil der Studierenden, deren Punktzahl mindestens fünf Punkte über der Grenze zwischen "bestanden" und "nicht bestanden" liegt (die 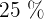 der Studierenden mit den niedrigsten Punktzahlen werden als "nicht bestanden" eingestuft)
der Studierenden mit den niedrigsten Punktzahlen werden als "nicht bestanden" eingestuft)
3 Wenn bekannt ist, dass die Punktzahl eines/r Studierenden höher als  , wie hoch ist dann die Wahrscheinlickeit, dass mehr als
, wie hoch ist dann die Wahrscheinlickeit, dass mehr als  Punkte erreicht wurden?
Punkte erreicht wurden?
1
Wir setzen die Werte in die Formel ein:
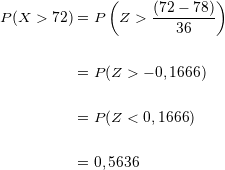
Die Wahrscheinlichkeit, dass eine Person eine Punktzahl von mehr als  in der Prüfung erreicht, liegt bei
in der Prüfung erreicht, liegt bei 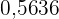 .
.
2
Wir setzen die Werte in die Formel ein:
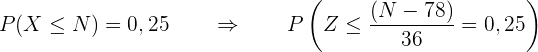
Wir suchen die Wahrscheinlickeit  in der Tabelle der Normalverteilung. Diese ist
in der Tabelle der Normalverteilung. Diese ist 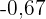 , was bedeutet, dass
, was bedeutet, dass
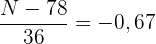
Wir bestimmen  :
:
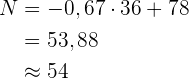
Wir berechnen für 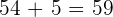 :
:
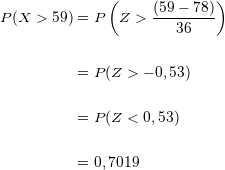
Der Prozentsatz der Studierenden, die bestehen und deren Punktzahl  Punkte oberhalb der Grenze zum Nichtbestehen liegen, beträgt
Punkte oberhalb der Grenze zum Nichtbestehen liegen, beträgt 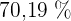 .
.
3
Wir setzen ein:
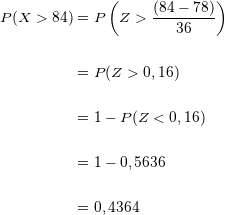
Aus der ersten Fragestellung dieser Aufgabe wissen wir, dass die Wahrscheinlichkeit, dass eine Person in der Prüfung mehr als  Punkte erreicht,
Punkte erreicht, 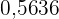 beträgt.
beträgt.
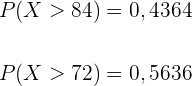
Nun wenden wir die Formel der bedingten Wahrscheinlichkeit an:
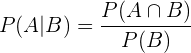
Wir setzen ein:
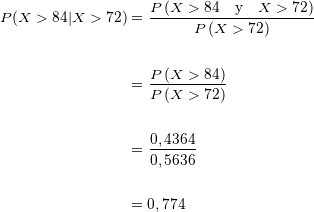
Die Wahrscheinlichkeit, dass eine Person, die mehr als  Punkte erreicht, auch mehr als
Punkte erreicht, auch mehr als  Punkte erreicht, liegt bei
Punkte erreicht, liegt bei 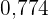 .
.
Die Normalverteilung für die Klassifizierung von Gruppen
Nach einem Test zur Allgemeinbildung wird festgestellt, dass die erzielten Ergebnisse einer Verteilung von 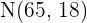 folgen.
folgen.
Die Teilnehmer*innen sollen in drei Gruppen eingeteilt werden (geringe Allgemeinbildung, akzeptable Allgemeinbildung, ausgezeichnete Allgemeinbildung), sodass 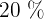 der Bevölkerung in der 1. Gruppe sind,
der Bevölkerung in der 1. Gruppe sind,  in der 2. Gruppe und
in der 2. Gruppe und  in der 3. Gruppe.
in der 3. Gruppe.
Welche Punkte sollten den Übergang von einer Gruppe zur anderen markieren?
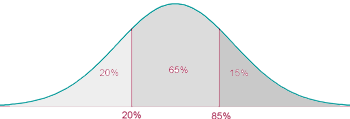
Wir suchen in unserer Tabelle den Parameter entsprechend der Wahrscheinlichkeit 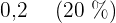 , der
, der 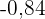 ist:
ist:

Wenn also  , gilt
, gilt
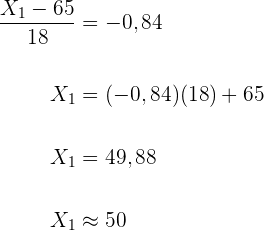
Wir suchen nun in unserer Tabelle den Parameter entsprechend der Wahrscheinlichkeit 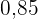 , der
, der 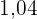 ist. Diese bedeutet, dass
ist. Diese bedeutet, dass

Wenn also 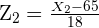 ist, gilt
ist, gilt
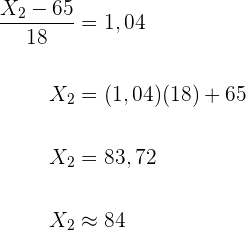
Geringe Allgemeinbildung bis  Punkte.
Punkte.
Akzeptable Allgemeinbildung zwischen  und
und  .
.
Ausgezeichnete Allgemeinbildung ab  Punkten.
Punkten.
Berechnung des Intelligenzquotienten mittels der Normalverteilung
Verschiedene Intelligenztests ergeben eine Punktzahl, die einer Normalverteilung mit einem Mittelwert von  und einer Standardabweichung von
und einer Standardabweichung von  folgt.
folgt.
1 Bestimme den Prozentsatz der Bevölkerung, der einen IQ zwischen  und
und  erhalten würde.
erhalten würde.
2 Welches auf  zentrierte Intervall enthält
zentrierte Intervall enthält 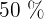 der Bevölkerung?
der Bevölkerung?
3 Es wird von einer Bevölkerung mit 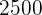 Personen ausgegangen. Wie viele Personen haben voraussichtlich einen IQ von mehr als
Personen ausgegangen. Wie viele Personen haben voraussichtlich einen IQ von mehr als  ?
?
Verschiedene Intelligenztests ergeben eine Punktzahl, die einer Normalverteilung mit einem Mittelwert von  und einer Standardabweichung von
und einer Standardabweichung von  folgt.
folgt.
1
Wir setzen die Werte in die Formel ein:
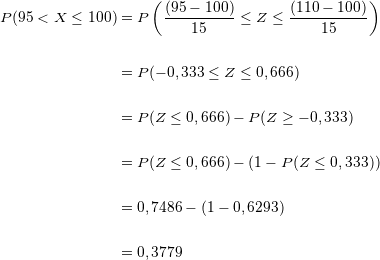
Der Prozentsatz der Bevölkerung, der einen IQ zwischen  und
und  hat, beträgt
hat, beträgt 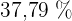 .
.
2
Da wir 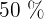 der Mitte der Bevölkerung nehmen möchten, nutzen wir das Intevall zwischen
der Mitte der Bevölkerung nehmen möchten, nutzen wir das Intevall zwischen 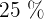 und
und  .
.
Wir suchen in unserer Tabelle den Paramter entsprechend der Wahrscheinlichkeit 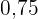 und
und 
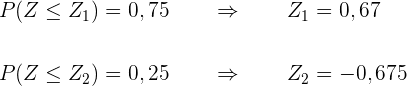
Wir setzen ein und bestimmen
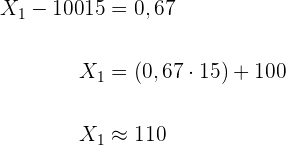
und
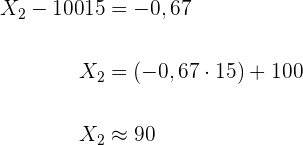
Somit ist das Intervall: 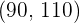 .
.
Das zentrierte Intervall, das 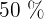 der Bevölkerung umfasst, liegt zwischen
der Bevölkerung umfasst, liegt zwischen  und
und  Punkten.
Punkten.
3
Wir setzen die Werte in die Formel ein, berechnen den Parameter und suchen die Wahrscheinlichkeit in der Tabelle
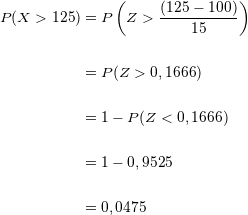
Diese Wahrscheinlichkeit multiplizieren wir mit den 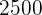 Personen. Wir erhalten:
Personen. Wir erhalten:
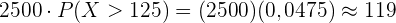
Von den 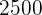 Personen haben voraussichtlich
Personen haben voraussichtlich 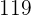 Personen einen IQ höher als
Personen einen IQ höher als  .
.
Verwendung der Normalverteilung zur Wahrscheinlichkeitsberechnung
In einer Stadt besitzt 1 von 3 Haushalten ein Telefon.
Es werden  Haushalte nach dem Zufallsprinzip ausgewählt. Berechne die Wahrscheinlichkeit, dass mindestens
Haushalte nach dem Zufallsprinzip ausgewählt. Berechne die Wahrscheinlichkeit, dass mindestens  von ihnen ein Telefon haben.
von ihnen ein Telefon haben.
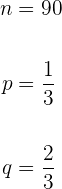
n: Anzahl der zur Auswahl stehenden Haushalte.
p: Wahrscheinlichkeit, einen Haushalt auszuwählen, der ein Telefon besitzt.
q: Komplement der Wahrscheinlichkeit.
Um diese Art von Aufgabe zu lösen, wenden wir den Satz von Moivre-Laplace an:
Wenn  eine binomialverteilte Zufallsvariable der Parameter
eine binomialverteilte Zufallsvariable der Parameter  und
und  ist,
ist, 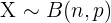 , dann kann
, dann kann  einer Normalverteilung mit dem Mittelwert
einer Normalverteilung mit dem Mittelwert  und der Standardabweichung
und der Standardabweichung 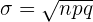 (wobei
(wobei 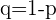 ) angenähert werden. Es müssen die beiden folgenden Bedingungen erfüllt sein:
) angenähert werden. Es müssen die beiden folgenden Bedingungen erfüllt sein:
Bedingung 1.  .
.
Bedingung 2. 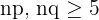 .
.
Dann würde die binomialverteilte Variable 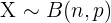 mit der Binomialverteilung
mit der Binomialverteilung  angenähert werden.
angenähert werden.
Da  , ist Bedingung 1 erfüllt.
, ist Bedingung 1 erfüllt.
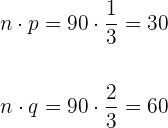
Somit ist Bedingung 2 erfüllt.
Wir wenden die Formel  an.
an.
Wir setzen ein:
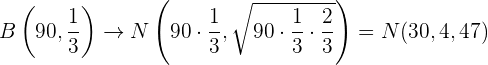
Nun wenden wir die Formel der Normalverteilung an
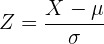
Wir setzen ein, berechnen und suchen den Wert der Wahrscheinlichkeit in unserer Normalverteilungstabelle:
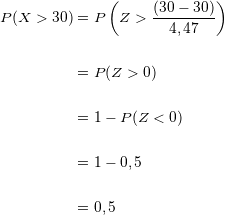
Bei einer Zufallsauswahl von  besteht eine Wahrscheinlichkeit von
besteht eine Wahrscheinlichkeit von  , dass mindestens
, dass mindestens  Haushalte, die ein Telefon besitzen, ausgewählt wurden.
Haushalte, die ein Telefon besitzen, ausgewählt wurden.
Wahrscheinlichkeit eines Ergeignisses mit Zufallsvariable
Bei einem Multiple-Choice-Test mit  Fragen gibt es auf jede Frage eine richtige und eine falsche Antwort.
Fragen gibt es auf jede Frage eine richtige und eine falsche Antwort.
Der Test ist bestanden, wenn mehr als  Fragen richtig beantwortet werden.
Fragen richtig beantwortet werden.
Berechne unter der Annahme einer zufälligen Beantwortung die Wahrscheinlichkeit, den Test zu bestehen.
Wir wenden den Satz von Moivre-Laplace an:
Wir überprüfen die  Bedingungen:
Bedingungen:
Erste Bedingung:
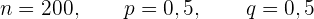
Zweite Bedingung: 
Da beide Bedingungen erfüllt sind, wenden wir die Formel an
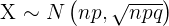 .
.
Wir setzen ein:
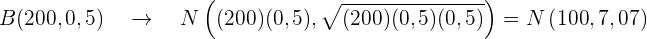
Nun wenden wir 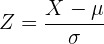 an
an
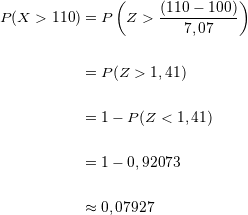
Bei der zufälligen Beantwortung eines Multiple-Choice-Tests besteht eine Wahrscheinlichkeit von 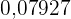 , den Test zu bestehen.
, den Test zu bestehen.
Normalverteilung für die Wahrscheinlichkeit
Eine Studie hat gezeigt, dass in einem bestimmten Stadtteil  der Haushalte mindestens zwei Fernseher besitzen. Nach dem Zufallsprinzip werden
der Haushalte mindestens zwei Fernseher besitzen. Nach dem Zufallsprinzip werden  Haushalte in genanntem Stadtteil ausgewählt.
Haushalte in genanntem Stadtteil ausgewählt.
Aufgabe:
1 Wie hoch ist die Wahrscheinlichkeit, dass mindestens  dieser Haushalte mindestens zwei Fernseher besitzen?
dieser Haushalte mindestens zwei Fernseher besitzen?
2 Wie hoch ist die Wahrscheinlichkeit, dass zwischen  und
und  Haushalte mindestens zwei Fernseher besitzen?
Haushalte mindestens zwei Fernseher besitzen?
1
Wir wenden den Satz von Moivre-Laplace an und überprüfen die  Bedingungen:
Bedingungen:
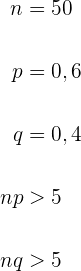
Da beide Bedingungen erfüllt sind, wenden wir die Formel  an.
an.
Wir setzen ein:
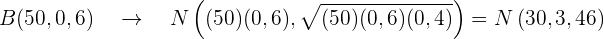
Wir wenden an: 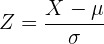 .
.
Und setzen ein:
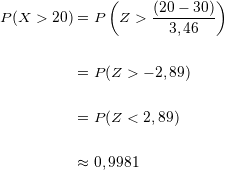
2
Wir wenden die Formel 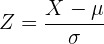 an und setzen den Wert des Mittelwerts
an und setzen den Wert des Mittelwerts 
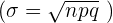 ein
ein
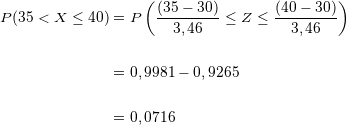
Die Wahrscheinlichkeit, dass zwischen  und
und  Haushalten mindestens
Haushalten mindestens  Fernseher besitzen, liegt bei
Fernseher besitzen, liegt bei 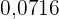 .
.
Mit KI zusammenfassen:













