Zur Erinnerung: Ein bestimmtes Integral bezieht sich auf ein bestimmtes Intervall eines Integrals, sodass sich der Vorgang sehr einfach zusammenfassen lässt:
Schritt 1: Führe die Integration der Funktion mithilfe der definierten Formeln durch.
Schritt 2: Werte das Ergebnis deiner Integration an beiden Grenzwerten aus.
Schritt 3 : Vom Ergebnis des größten Punktes des Intervalls musst du das Ergebnis des kleinsten Punktes des Intervalls subtrahieren.
Beispiel:
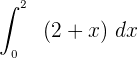
Wir wenden die Formeln an, um die Funktion 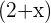 zu integrieren:
zu integrieren:
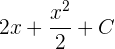
Nun muss diese Funktion an den Punkten 0 und 2 ausgewertet werden:
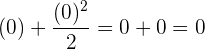
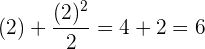
Wir subtrahieren jetzt vom höchsten Grenzwert den niedrigsten Grenzwert des Intervalls.
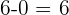
Das bestimmte Integral in diesem Intervall ist 6. Das bedeutet, dass die Fläche unter dem Graphen dieser Gleichung allein in diesem Intervall 6 Einheiten beträgt.
Bestimmtes Integral eines Bruchs
Wir wenden die Formel für die Integration von Brüchen an: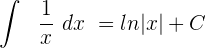
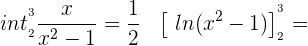

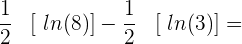
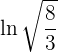
Bestimmtes Integral eines Polynom 3. Grades

Da es sich um ein Polynom handelt, d. h. um unterschiedliche algebraische Terme, die addiert oder subtrahiert werden, können wir einen nach dem anderen integrieren:
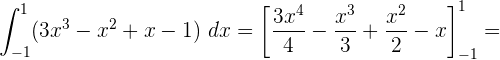
Nachdem wir das Ergebnis bei 1 und -1 ausgewertet haben, führen wir die Addition durch:
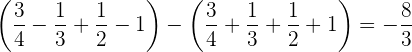
Bestimmtes Integral von 1 bis e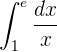
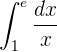
Beachte:
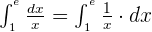
Somit können wir für das Integral die folgende Formel verwenden:
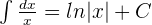
Wir werten bei 1 und e aus. Im Anschluss subtrahieren wir

Bestimmtes Integral einer Sinusfunktion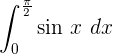
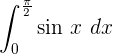
Die Formel für die Integration des Sinus lautet:
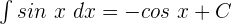
Und somit:
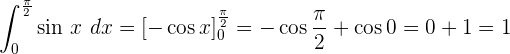
Bestimmtes Integral von trigonometrischen Funktionen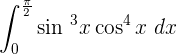
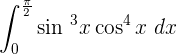
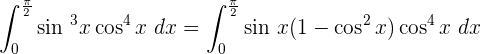
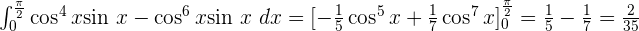
Bestimmtes Integral eines Logarithmus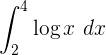
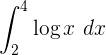
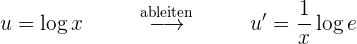
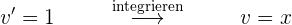
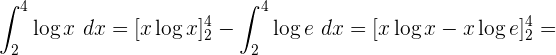
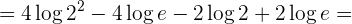
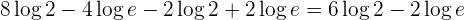
Bestimmtes Integral im Intervall [0 , n²]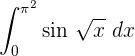
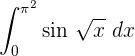
Wir berechnen das bestimmte Integral durch Substitution.
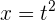
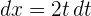
Wir ermitteln die neuen Integrationsgrenzen.
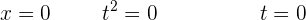
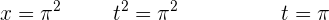
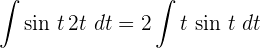
Wir integrieren partiell.
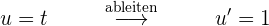
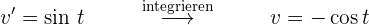
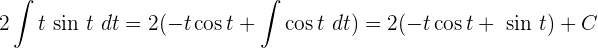
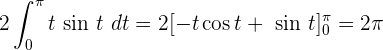
Dies kann auch ohne Umwandlung der Integrationsgrenzen und Rückkehr zur Ausgangsvariablen erfolgen.
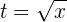
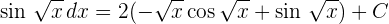
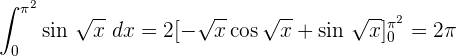
Berechne die Ableitung der folgenden Funktionen
1 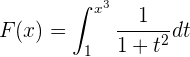
2 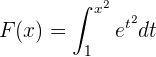
1 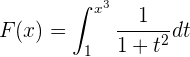
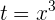
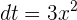
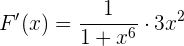
2 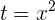
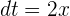
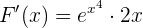
Mittelwertsatz der Integralrechnung
Kann bei der folgenden Funktion der Mittelwertsatz der Interalrechnung im Intervall [0, 1] angewendet werden?
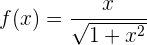
Kann bei der folgenden Funktion der Mittelwertsatz der Interalrechnung im Intervall [0, 1] angewendet werden?
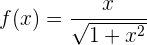
Da die Funktion bei [0, 1] stetig ist, kann der Mittelwertsatz angewendet werden.

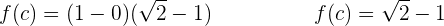

Mit KI zusammenfassen:


