Kapitel

Eigenschaften von Determinanten
Zeige, dass die folgenden Determinanten einen Wert von 0 haben:

1 Determinante von A Zu Spalte 3 addieren wir Spalte 2 und erhalten: 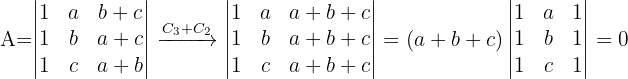 Sie hat zwei gleiche Spalten, also muss ihre Determinante gleich 0 sein.
Sie hat zwei gleiche Spalten, also muss ihre Determinante gleich 0 sein.
2 Determinante von B
Wir stellen fest, dass die dritte Spalte gleich der Summe der beiden anderen ist, ihre Determinante ist also 0. 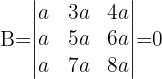
Wenn 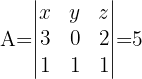 , berechne die Determinanten von
, berechne die Determinanten von  und
und 
1 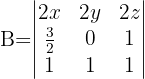
2 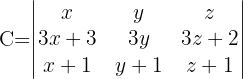
1 Determinante von B 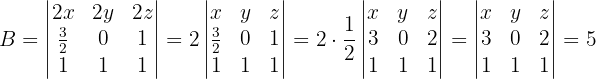
2 Determinante von C
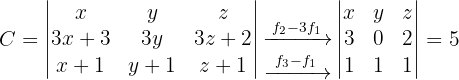
Zeige, dass die folgenden Determinanten Vielfache von 5 bzw. 4 sind

1 Determinante von A

Der genaue Wert der letzten Matrix interessiert uns nicht, da wir wissen, dass er eine ganze Zahl sein muss und dass die Determinante von  ein Vielfaches von 5 ist, wenn sie mit der 5 auf der linken Seite multipliziert wird.
ein Vielfaches von 5 ist, wenn sie mit der 5 auf der linken Seite multipliziert wird.
2 Determinante von B
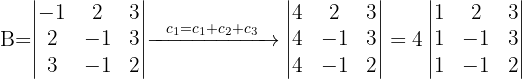
Ebenso ignorieren wir den genauen Wert der letzten Matrix, da die Determinante von  ein Vielfaches von 4 ist, da sie eine ganze Zahl ist und mit der 4 auf der linken Seite multipliziert wird.
ein Vielfaches von 4 ist, da sie eine ganze Zahl ist und mit der 4 auf der linken Seite multipliziert wird.
Zeige, dass die folgende Determinante ein Vielfaches von 15 ist:
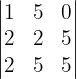
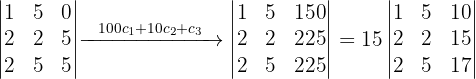
Der genaue Wert der letzten Matrix interessiert uns nicht, weil wir wissen, dass es eine ganze Zahl sein muss und dass die Determinante von ein Vielfaches von 15 ist, wenn sie mit der 15 auf der linken Seite multipliziert wird.
Beweise die dargestellten Gleichheiten, ohne dass die Determinanten weiter bearbeitet werden müssen:
1 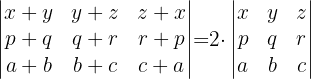
2 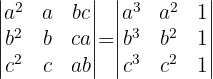
1 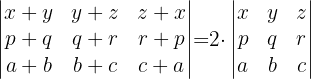
Wir drücken die Matrix als Summe von zwei Matrizen aus
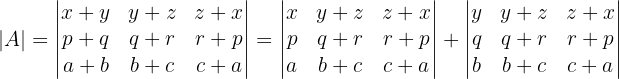
Jeder dieser Summanden ist wiederum die Summe von zwei anderen Matrizen
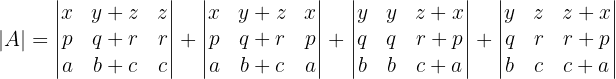
Die zweite und die dritte Matrize haben jedoch zwei gleiche Spalten, so dass ihre Determinante gleich 0 ist. Also
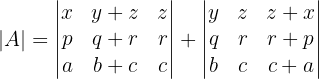
Wir trennen diese beiden Matrizen wieder als Summen und es bleibt
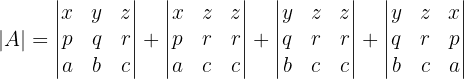
Auch hier haben die zweite und die dritte Matrize zwei gleiche Spalten, so dass ihre Determinante gleich 0 ist.
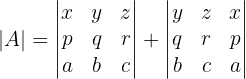
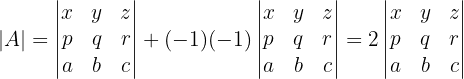
Jeder Faktor  ergibt sich aus der Vertauschung der Position eines Spaltenpaares.
ergibt sich aus der Vertauschung der Position eines Spaltenpaares.
2 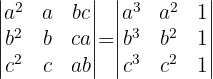
Wir multiplizieren die 1. Zeile mit  , die 2. mit
, die 2. mit  und die 3. mit
und die 3. mit  . Daher müssen wir durch abc dividieren, damit sich das Ergebnis nicht ändert.
. Daher müssen wir durch abc dividieren, damit sich das Ergebnis nicht ändert. 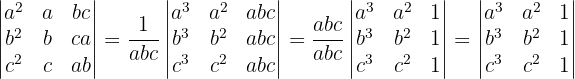
Berechne unter Anwendung der Eigenschaften der Determinanten:

1 Determinante A
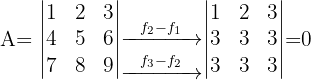
2 Determinante B
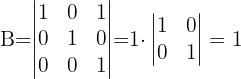
3 Determinante C
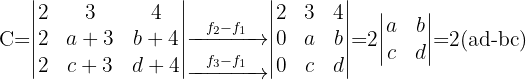
Gleichungen und Determinanten
Löse die folgenden Gleichungen, ohne die Determinanten zu bearbeiten.
1 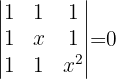
2 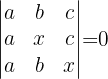
1 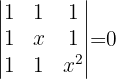
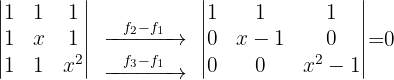
Wir berechnen die Determinante und erhalten die Gleichung
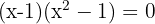
Die Lösungen sind also

2 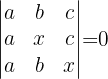
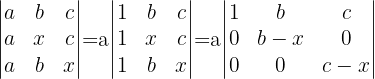
Aus der Berechnung der Determinante ergibt sich

Die Lösungen sind

Löse die folgenden Matrizengleichungen:
1  , wobei
, wobei 
2 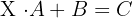 , wobei
, wobei
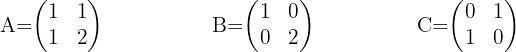
1 
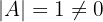 , es existiert die inverse Matrix
, es existiert die inverse Matrix 
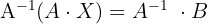
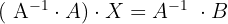
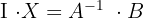
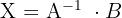
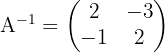
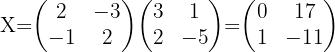
2 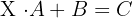
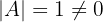 , es existiert die inverse Matrix
, es existiert die inverse Matrix 

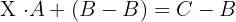



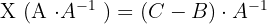
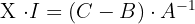

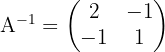
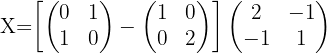
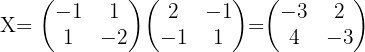
Determinante einer Dreiecksmatrix
Berechne die Determinante der Dreicksmatrix:
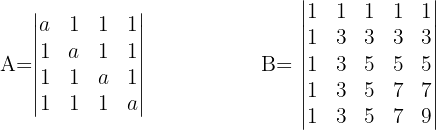
1 Determinante A
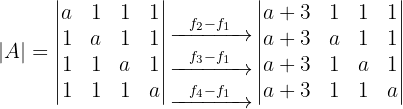

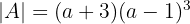
2 Determinante B
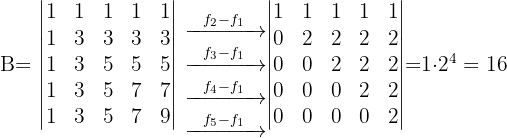
Vandermonde-Determinante
Berechne die Vandermonde-Determinanten:
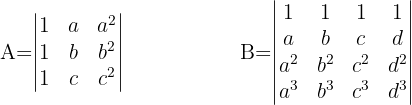
1 Determinante A
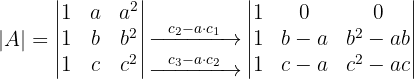
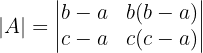
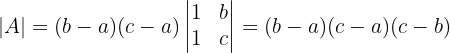
2 Determinante B
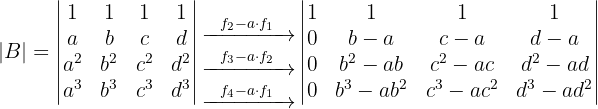
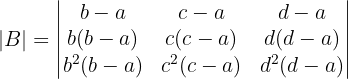
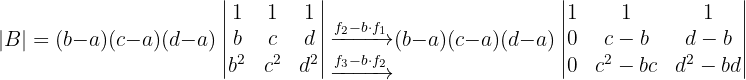
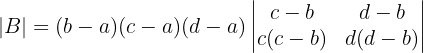
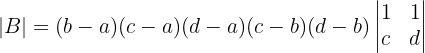
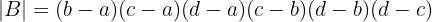
Inverse Matrix
Berechne die inverse Matrix:
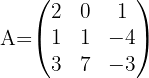
Berechne die inverse Matrix von:
Die Determinate ist 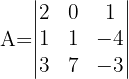
Die Adjunkte und die transponierte Adjunkte sind gegeben durch
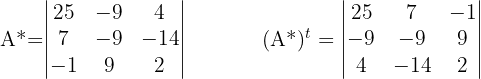
Schließlich ist die inverse Matrix
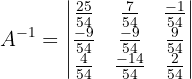
Für welche Werte von  der Matrix
der Matrix 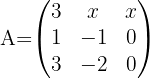 gibt es keine inverse Matrix?
gibt es keine inverse Matrix?
Wir berechnen die Determinante
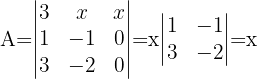
Für  hat die Matrix
hat die Matrix  keine inverse Matrix.
keine inverse Matrix.
Rang von Matrizen
Berechne den Rang der folgenden Matrizen:
1 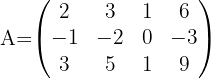
2 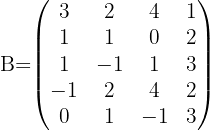
3 
1 Rang von A
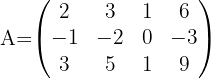
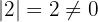
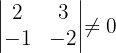


Somit ist der Rang
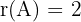
2 Rang von B
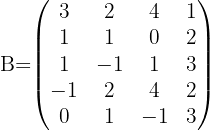
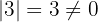
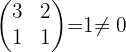
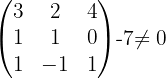
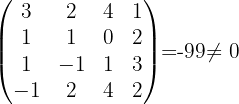
Somit ist der Rang von  gegeben durch
gegeben durch

3 Rang von C

Wir streichen die dritte Spalte, weil sie 0 ist, die vierte, weil sie proportional zur ersten ist, und die fünfte, weil sie eine lineare Kombination der ersten und zweiten ist:
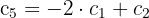
Der Rang von  ist äquivalent zum Rang der folgenden Matrix
ist äquivalent zum Rang der folgenden Matrix
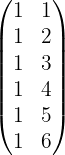

Der Rang von  ist
ist
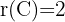
Mit KI zusammenfassen:












