Kapitel
Definition einer Determinante
Jeder quadratischen Matrix 
ist ein spezifischer Skalar, die sogenannte Determinante von zugeordnet, die als 
oder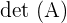 
dargestellt wird. Sie lässt sich anhand der Einträge der Matrix berechnen und charakterisiert ihre Eigenschaften. Zum Beispiel ist die Determinante von nur dann ungleich null, wenn invertierbar ist.
Im Folgenden erfährst du, wie sich der Wert der Determinanten von Matrizen der Ordnung 
oder kleiner berechnen lässt.
Determinanten erster Ordnung
Beispiel: Determinante einer 1x1-Matrix
,
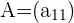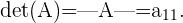
Determinanten zweiter Ordnung
Beispiel: Determinante einer 2x2-Matrix
,
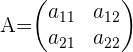
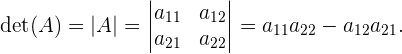
Determinanten dritter Ordnung
Beispiel: Determinante einer 3x3-Matrix
,
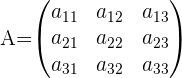
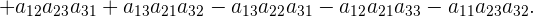
Die Regel von Sarrus
Die Regel von Sarrus ist ein Algorythmus, der leicht einzuprägen ist und dient dazu, die Determinante einer 
-Matrix zu berechnen.
Zur Auflösung müssen anhand der folgenden Schritte positive und negative Faktoren multipliziert werden.
Die Terme mit positivem Vorzeichen werden aus den Elementen der Hauptdiagonale sowie den Elementen der Nebendiagonalen und deren entsprechenden Gegendiagonalen gebildet.
Folgende Elemente der Matrix sind miteinander zu multiplizieren.
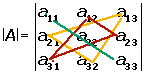
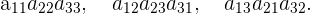
Die Terme mit negativem Vorzeichen werden aus den Elementen der ersten Nebendiagonale sowie der weiteren Nebendiagonalen und deren entsprechenden Gegendiagonalen gebildet.
Folgende Elemente der Matrix sind miteinander zu multiplizieren.
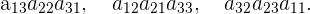
Komplementärer Minor
Der Wert einer Determinante der Ordnung 
, den man erhält, indem man die Zeile 
und die Spalte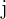 
in der Matrix aufhebt, wird als komplementärer Minor eines Elementes 
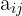bezeichnet.
Nebengruppe
Die Nebengruppe des Elements 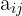wird durch Voranstellen als komplementäre Nebengruppe bezeichnet:
- das Vorzeichen ist
, wenn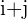 
gerade ist. - das Vorzeichen ist
, wenn 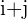ungerade ist.
Der Wert einer Determinante ist gleich der Summe der Produkte der Elemente einer Zeile mit ihren entsprechenden Nebengruppen:
Determinanten der Ordnung 3 und höher
Die Determinante einer Matrix der Ordnung und höher kann in folgenden Schritten berechnet werden:
1 Wenn in einer der Zeilen oder Spalten der Matrix alle Elemente gleich Null sind, ist auch der Wert der Determinante Null.
2 Wenn es keine Nullzeilen oder -spalten gibt, sehen wir uns die erste Zeile an.
3 Bei einem Element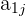 
in der ersten Zeile berechnet sich die Determinante der Matrix, indem man die Zeile 
und die Spalte 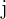der Matrix aufhebt.
4 Man multipliziert den Wert der in Schritt 3 berechneten Determinante mit der Zahl 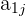und wiederholen das für jedes Element 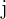der Matrix 
5 Anschließend addiert und subtrahiert man die in den vorherigen Schritten berechneten Werte abwechselnd. Das heißt, der Wert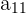 
der Determinante der Matrix, die sich aus dem Aufheben der Zeile und der Spalte ergibt, erhält ein positives Vorzeichen; der folgende Wert erhält ein negatives Vorzeichen, der folgende ein positives, und so weiter. Als Endergebnis erhält man die Determinante der Matrix
Eigenschaften von Determinanten
Bei einer Matrix 
sei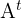 
ihre Transponierte.
1 
2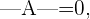 
, wenn eine der folgenden Aussagen zutrifft: die Matrix enthält zwei gleiche Zeilen, alle Elemente einer Zeile sind gleich Null oder die Elemente einer Zeile sind eine lineare Kombination anderer Zeilen.
3 Eine Dreiecksdeterminante ergibt sich aus dem Produkt der Elemente der Hauptdiagonalen, wobei als Dreiecksmatrix eine Matrix bezeichnet wird, in der alle Elemente oberhalb oder unterhalb der Hauptdiagonale gleich Null sind.
4 Wenn zwei parallele Linien in einer Determinante gegeneinander vertauscht werden, ändert sich das Vorzeichen der Determinante.
5 Addiert man die Elemente einer Linie mit den Elementen einer einer parallelen Linie, die vorab mit einer reellen Zahl multipliziert wurden, ändert sich der Wert der Determinante nicht.
6 Wenn eine Determinante mit einer reellen Zahl multipliziert wird, kann das Produkt aus jeder beliebigen Zeile gebildet werden, jedoch nur aus einer.
7 Wenn alle Elemente einer Zeile oder Spalte aus zwei Summanden bestehen, wird die Determinante in die Summe von zwei Determinanten zerlegt.
8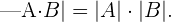 
Inverse Matrix
Bei einer Matrix sei die Inverse
in welcher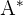 
die Adjunkte von ist.
Rang einer Matrix
Der Rang einer Matrix wird durch die Ordnung der größten quadratischen Unterdeterminante bestimmt, die ungleich Null ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
