Berechne den Wert der Determinante

1 Die erste Zeile ist ein Vielfaches von 2, das heißt
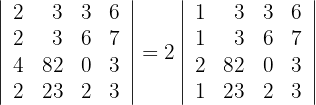
2 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 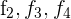 durch
durch 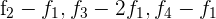 und du erhältst
und du erhältst
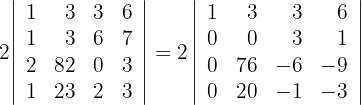
3 Zur Berechnung der ersten Spalte wenden wir die obere Dreiecksformel an und erhalten
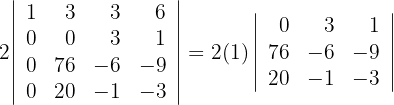
4
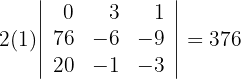
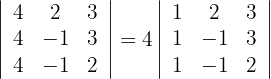
Berechne mithilfe der Rechenregeln für Determinanten:
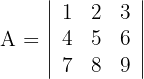
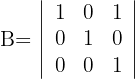
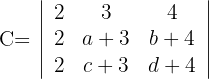
1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 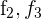 durch
durch  und du erhältst
und du erhältst
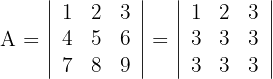
2 Da zwei Zeilen genau gleich sind, ist nach der Rechenregel für Determinanten die Lösung gleich Null
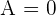
2 Determinante B
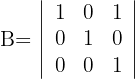
1 Hier handelt es scih um eine Matrix mit reduzierter Zeilenstufenform. Anhand der Rechenregel für Determinanten erhält man das Ergebnis, indem man die Elemente der Hauptdiagonalen miteinander multipliziert
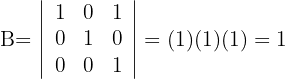
3 Determinante C
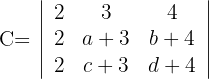
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 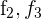 durch
durch 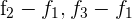 und du erhältst
und du erhältst
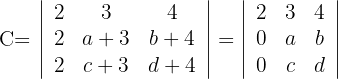
2 Für die erste Spalte mit zwei Nullen wenden wir die Regel für Matrizen mit reduzierter Struktur an und erhalten
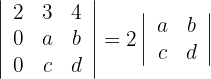
3 Berechne die letzte Determinante und du erhältst
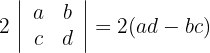
Wende die Rechenregeln für Determinanten an und berechne:


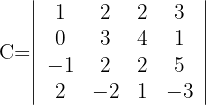
1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 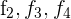 durch
durch 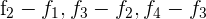 respectivamente y obtenemos
respectivamente y obtenemos

2 Ersetze noch einmal die Zeilen 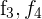 durch
durch 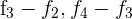 und du erhältst entsprechend
und du erhältst entsprechend
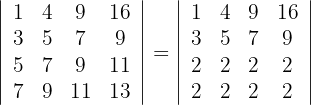
3 Da zwei Zeilen genau gleich sind, ist nach der Rechenregel für Determinanten die Lösung gleich Null, das heißt 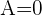
2 Determinante B
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen columnas 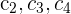 durch
durch  und du erhältst
und du erhältst
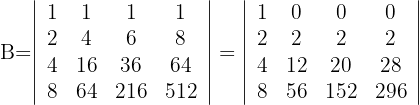
2 Wende für die Berechnung der ersten Zeile mit drei Nullen die Regel für reduzierte Matrizen an
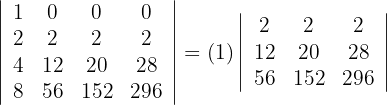
3 Die erste Zeile ist ein Vielfaches von 2, das heißt
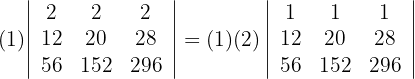
4 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Spalten 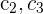 durch
durch 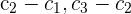 und du erhältst
und du erhältst
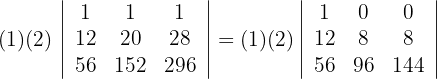
5 Wende für die Berechnung der ersten Zeile mit zwei Nullen die Regel für reduzierte Matrizen an
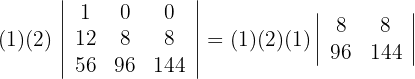
6 Berechne die Determinante der 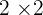 -Matrix
-Matrix
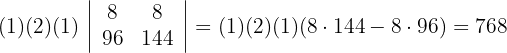
3 Determinante C
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 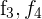 durch
durch 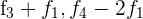 und du erhältst
und du erhältst
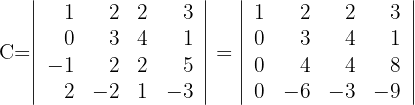
2 Wende für die Berechnung der ersten Spalte mit drei Nullen die Regel für reduzierte Matrizen an
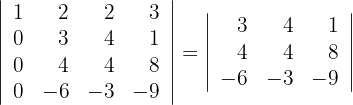
3 Die zweite Zeile ist ein Vielfaches von 4 und die dritte ein Vielfaches von -3, das heißt
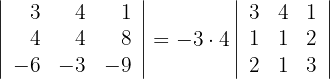
4 Berechne die letzte Determinante
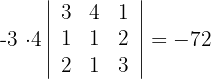
Berechne den Wert der folgenden Dreiecksdeterminanten:
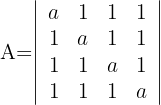

1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Spalten 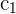 durch
durch  und du erhältst
und du erhältst
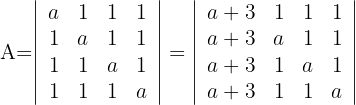
2 Die erste Spalte ist ein Vielfaches von  , das heißt
, das heißt
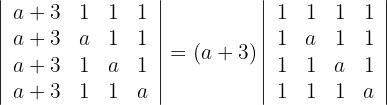
3 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 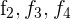 durch
durch  und du erhältst
und du erhältst
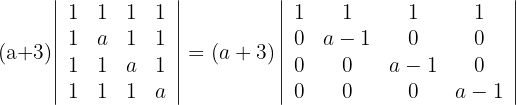
4 Die Determinante einer Dreiecksmatrix ist gleich dem Produkt der Elemente ihrer Diagonalen
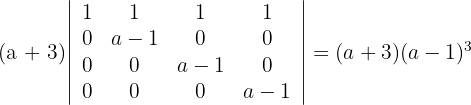
2 Determinante B
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen  durch
durch 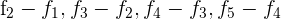 und du erhältst
und du erhältst
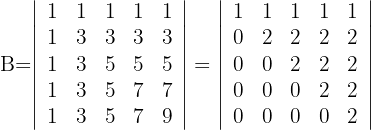
2 Die Determinante einer Dreiecksmatrix ist gleich dem Produkt der Elemente ihrer Diagonalen
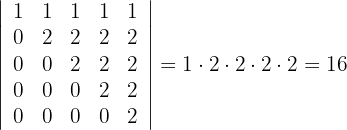
Berechne die Vandermondesche Determinante:
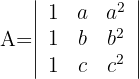
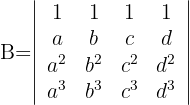
1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Spalten 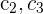 durch
durch 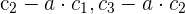 und du erhältst
und du erhältst
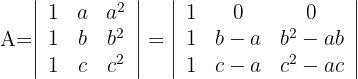
2 Wende für die Berechnung der ersten Zeile mit drei Nullen die Regel für reduzierte Matrizen an
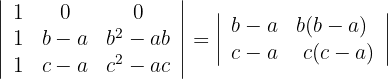
3 Die Elemente der ersten Zeile haben einen gemeinsamen Faktor. Ebenso die der zweiten Zeile. Ziehe diese gemeinsamen Faktoren aus der Determinante und löse die Determinante:
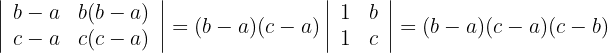
2 Determinante B
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 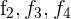 durch
durch 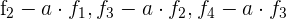 und du erhältst
und du erhältst
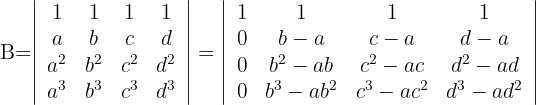
2 Wende für die Berechnung der ersten Spalte mit drei Nullen die Regel für reduzierte Matrizen an
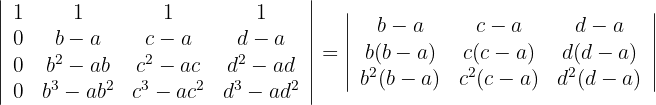
3 Ziehe den gemeinsamen Faktor aus jeder einzelnen der Spalten und löse die Determinante
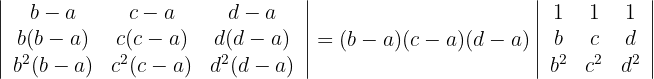
4 Ersetze 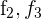 durch
durch 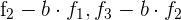 und du erhältst
und du erhältst
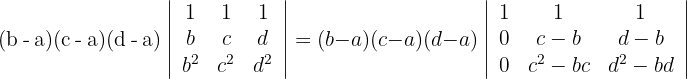
5 Wende für die Berechnung der ersten Spalte mit drei Nullen die Regel für reduzierte Matrizen an
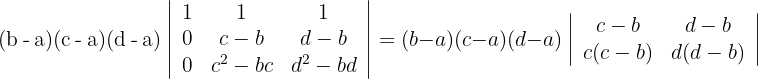
6 Ziehe den gemeinsamen Faktor aus der ersten und zweiten Spaltn und löse die Determinante
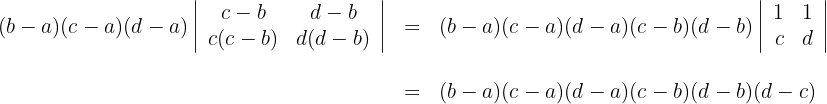
Berechne den Wert der folgenden Determinanten:


1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Spalten 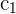 durch
durch 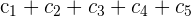 und du erhältst
und du erhältst
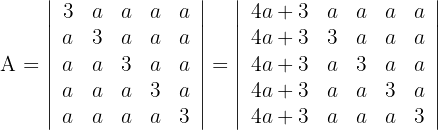
2 Die erste Spalte ist ein Vielfaches von  , das heißt
, das heißt
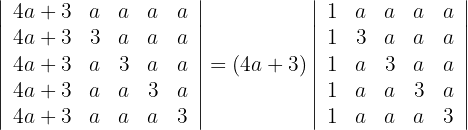
3 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen  durch
durch 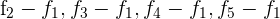 und du erhältst
und du erhältst
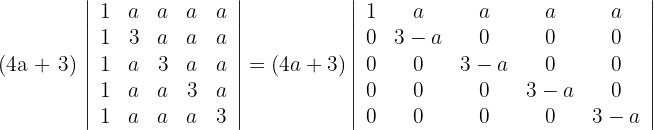
4 Die determinante einer Dreiecksmatrix ist gleich dem Produkt der Elemente ihrer Diagonalen
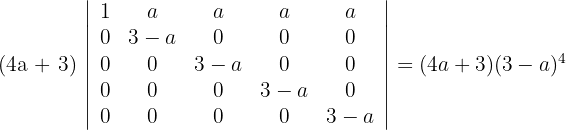
2 Determinante B
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen 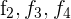 durch
durch 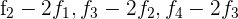 und du erhältst
und du erhältst
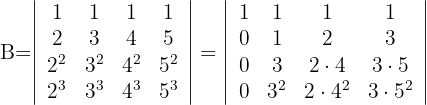
2 Wende für die Berechnung der ersten Spalte mit drei Nullen die Regel für reduzierte Matrizen an
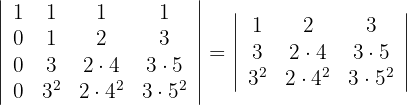
3 Die zweite Spalte ist ein Vielfaches von  und die dritte Spalte ein Vielfaches von
und die dritte Spalte ein Vielfaches von  , das heißt
, das heißt
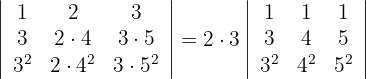
4 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Zeilen  durch
durch  und du erhältst
und du erhältst
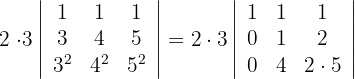
5 Wende für die Berechnung der ersten Spalte mit zwei Nullen die Regel für reduzierte Matrizen an
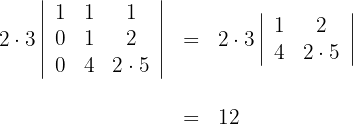
Beweise ohne aufzulösen, dass der Wert der folgenden Determinanten gleich Null ist:
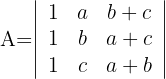
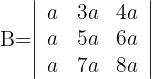
1 Determinante A
1 Da sich der Wert der Determinante bei einer Linearkombination nicht verändert, ersetze die Spalten 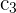 durch
durch 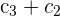 und du erhältst
und du erhältst
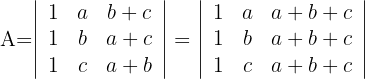
2 Die dritte Spalte enthält einen gemeinsamen Faktor, das heißt
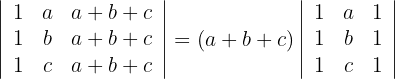
3 Die erste und dritte Spalte sind gleich, das heißt, die Determinante ist gleich Null
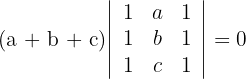
2 Determinante B
1 Die dritte Spalte ist gleich die Summe der ersten und zweiten, das heißt, die Determinante ist gleich Null
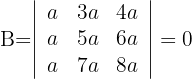
Gegeben sei die Determinante
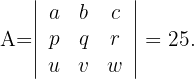
Berechne den Wert von
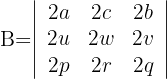
1 Da die Zeilen 2 als gemeinsamen Faktor haben, ist
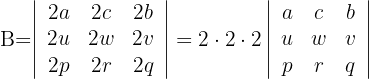
2 Tausche die Spalten 2 und 3 miteinander aus
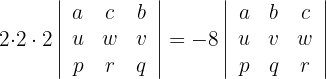
3 Tausche die Spalten 2 und 3 miteinander aus
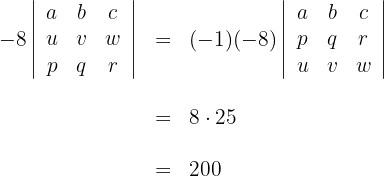
Gegeben sei 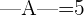 . Berechne die folgenden Determinanten:
. Berechne die folgenden Determinanten:
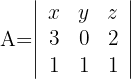
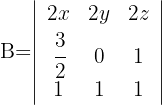
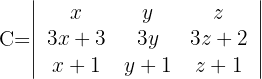
Determinante B
1 Zeile eins und zwei besitzen einen gemeinsamen Faktor
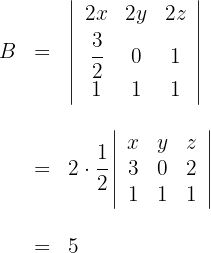
Determinante C
2 Ersetze die Zeilen 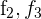 durch
durch 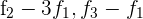
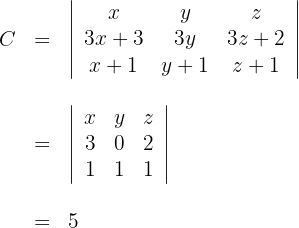
Beweise ohne aufzulösen, dass die folgenden Determinanten Vielfache von 5 bzw. 4 sind
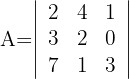
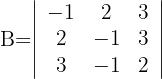
1 Determinante A
1 Ersetze die Spalte 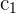 durch
durch 
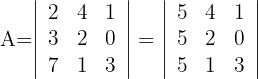
2 Die Spalte 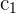 hat 5 als gemeinsamen Faktor
hat 5 als gemeinsamen Faktor
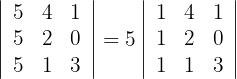
Die Determinante ist ein Vielfaches von 5
2 Determinante B
1 Ersetze die erste Spalte 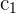 durch
durch 
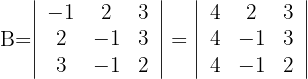
2 Die Spalte 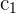 hat 4 als gemeinsamen Faktor
hat 4 als gemeinsamen Faktor
Die Determinante ist ein Vielfaches von 4.
Beweise ohne aufzulösen, dass die folgende Determinante ein Vielfaches von 15 ist:
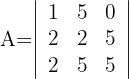
1 Ersetze die Spalte  durch
durch 
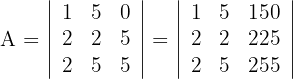
2 Die Spalte  hat 15 als gemeinsamen Faktor
hat 15 als gemeinsamen Faktor
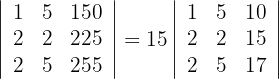
Die Determinante ist ein Vielfaches von 15.
Beweise, das die folgende Determinante durch 21 teilbar ist:

1 Ersetze die Spalte 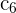 durch
durch 

2 Die Spalte 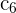 hat 21 als gemeinsamen Faktor
hat 21 als gemeinsamen Faktor

Die Determinante ist ein Vielfaches von 21, das heißt, sie ist durch 21 teilbar.
Zu beweisen sei die Gleichheit der folgenden Determinanten, ohne diese aufzulösen:
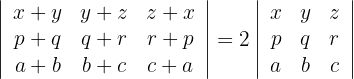
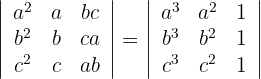
1 Erste Gleichheit
1 Die Spalten der ersten Determinante enthalten jeweils zwei Summanden, das heißt, man kann die Determinante als Addition aus zwei Determinanten mit jeweils einem der Summanden aus der ersten Spalte schreiben. Alle restlichen Elemente bleiben gleich. Führe dies für die erste Spalte durch:
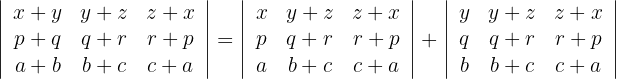
2 Führe diesen Vorgang nun für alle anderen Spalten durch
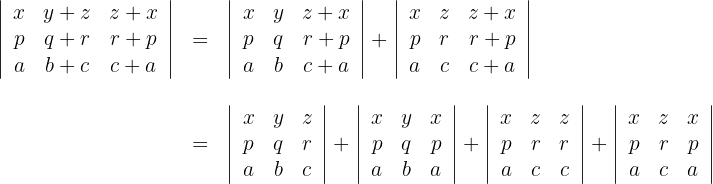
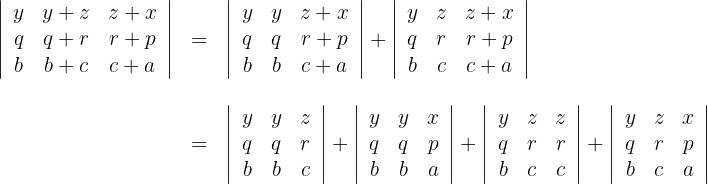
3 ist diese gleich Null, das heißt man erhält
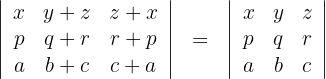
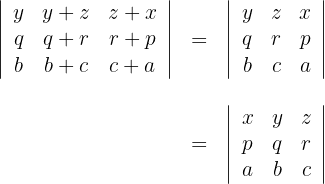
4 Die Gleichheit der beiden ursprünglichen Determinanten ist also bewiesen.
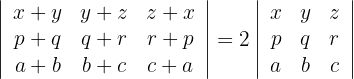
2 Zweite Gleichheit
1 Multipliziere die erste Zeile mit  , die zweite mit
, die zweite mit  und die dritte mit
und die dritte mit  . Um die Gleichheit beizubehalten, multipliziere mit
. Um die Gleichheit beizubehalten, multipliziere mit 
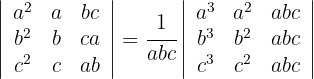
2 In der dritten Spalte liegt ein gemeinsamer Faktor vor
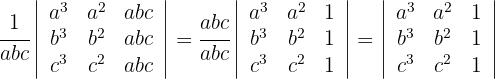
Löse die folgenden Gleichungen ohne die Determinante aufzulösen
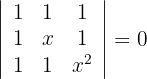
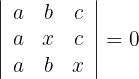
1 Erste Gleichung
1 Ersetze die Zeilen 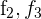 durch
durch 
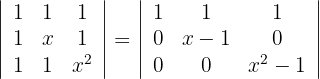
2 Hier liegt eine Dreiecksmatrix vor, das heißt, die Determinante ist gleich dem Produkt ihrer Diagonalen
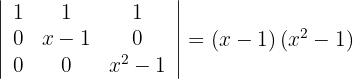
3 Da die Determinante gleich Null ist, erhält man 
2 Zweite Gleichung
1 Die erste Spalte enthält einen gemeinsamen Faktor
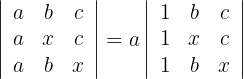
2 Ersetze die Zeilen 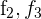 durch
durch 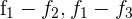
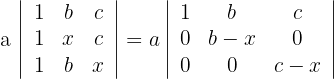
3Hier liegt eine Dreiecksmatrix vor, das heißt, die Determinante ist gleich dem Produkt ihrer Diagonalen
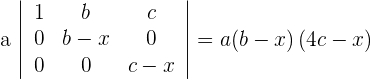
Da die Determinante gleich Null ist, ist 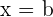 und
und 
Finde die inverse Matrix von:
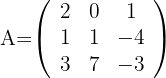
1 Berechne die Determinante
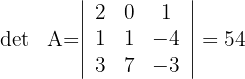
2 Berechne die adjunkte Matrix
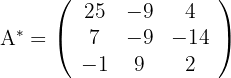
3 Berechne die Transponierte
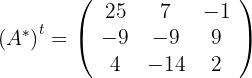
4 Die Inverse setzt sich aus  zusammen
zusammen
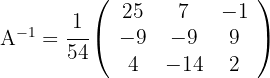
Für welche Werte von  gibt es zur Matrix
gibt es zur Matrix
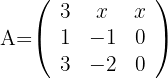
keine inverse Matrix?
1 Berechne die Determinante, indem du sie auf Basis der dritten Spalte vereinfachst
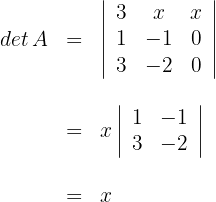
2 Eine Matrix besitzt keine Inverse, wenn ihre Determinante gleich Null ist. Das heißt, die Matrix  hat keine Inverse für
hat keine Inverse für 
Für welche Werte von  besitzt die Matrix
besitzt die Matrix
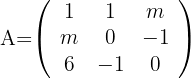
keine inverse Matrix?
1 Berechne die Determinante
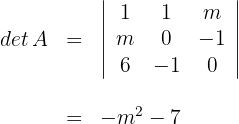
2 Eine Matrix besitzt keine Inverse, wenn ihre Determinante gleich Null ist. Die Determinante 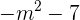 ist für jeden reellen Wert von
ist für jeden reellen Wert von  negativ. Das heißt, die Matrix
negativ. Das heißt, die Matrix  besitzt immer eine Inverse, unabhängig vom reellen Wert von
besitzt immer eine Inverse, unabhängig vom reellen Wert von 
Berechne den Rang der folgenden Matrizen:
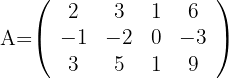
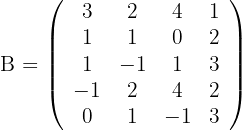

1 Rang von 
1 Berechne die Determinanten der Untermatrizen ersten Ranges
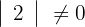
2 Berechne die Determinanten der Untermatrizen zweiten Ranges
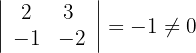
3Berechne die Determinanten der Untermatrizen dritten Ranges
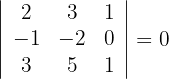
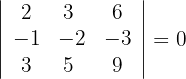
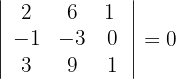
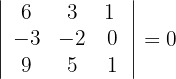
4 Der Rang der Matrix ist folglich 2.
2 Rang von 
1 Berechne die Determinanten der Untermatrizen ersten Ranges
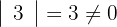
2 Berechne die Determinanten der Untermatrizen zweiten Ranges
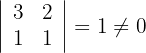
3 Berechne die Determinanten der Untermatrizen dritten Ranges
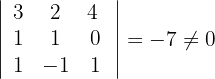
4 Berechne die Determinanten der Untermatrizen vierten Ranges
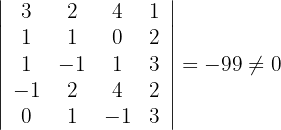
5 Der Rang der Matrix ist folglich 4.
3 Rang von 
1 Eliminiere die dritte Spalte, da sie gleich Null ist, die vierte, da sie proportional zur ersten ist und die fünfte, da sie eine Linearkombination der ersten und zweiten ist 

2 Berechne die Determinanten der Untermatrizen ersten Ranges
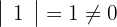
3 Berechne die Determinanten der Untermatrizen zweiten Ranges
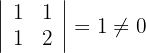
4 Der Rang der Matrix ist folglich 2.
Löse die folgenden Matrixgleichungen
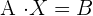
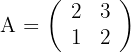
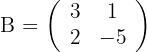
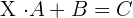
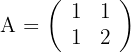
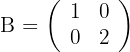
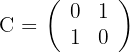
1 Erste Gleichung
1 Die Determinante von  ist ungleich Null, das heißt, sie besitzt eine Inverse
ist ungleich Null, das heißt, sie besitzt eine Inverse
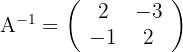
2 Löse die Gleichung
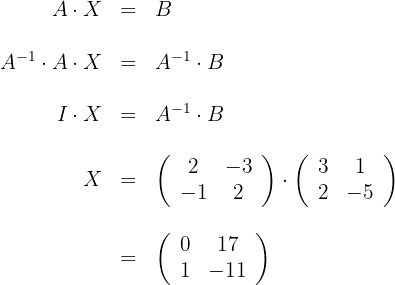
2 Zweite Gleichung
1 Die Determinante von  ist ungleich Null, das heißt, sie besitzt eine Inverse
ist ungleich Null, das heißt, sie besitzt eine Inverse
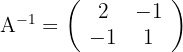
2 Löse die Gleichung
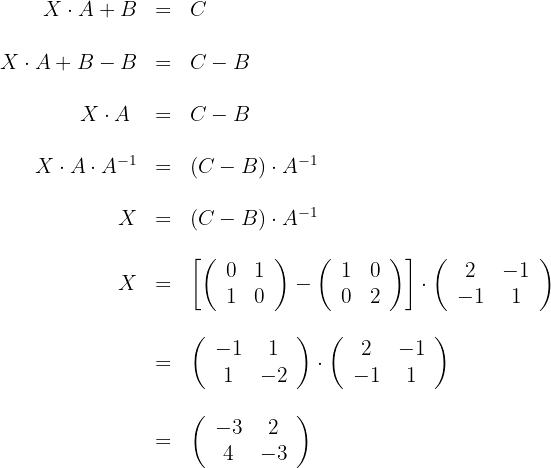
Löse die folgende Matrixgleichung

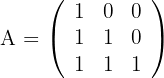

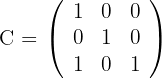
1 Die Determinante von  ist ungleich Null, das heißt, sie besitzt eine Inverse
ist ungleich Null, das heißt, sie besitzt eine Inverse
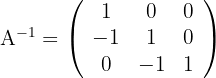
2 Löse die Gleichung
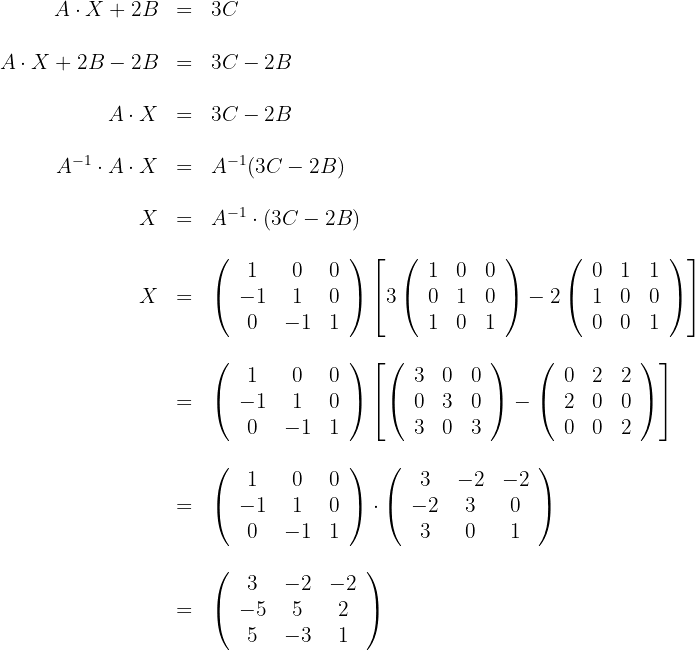
Mit KI zusammenfassen:



