Pierre Sarrus (1798–1861) war ein französischer Mathematiker, der eine Regel zur Berechnung
von Determinanten der Ordnung 3 aufstellte.
Was ist die Regel von Sarrus?
Die Regel von Sarrus ist ein Verfahren oder Algorithmus zur Berechnung der Determinante einer Matrix der Dimension 
.
Dieser Vorgang ist einfach und leicht zu merken und wird im Folgenden beschrieben.
Gegeben ist eine Matrix
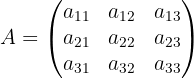
Im Folgenden beschreiben wir die Methode zur Berechnung von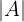 
.
Schritt 1: Bilde eine neue Matrix mit 5 Zeilen, indem du die ersten beiden Zeilen unterhalb der
Ausgangsmatrix wiederholst:
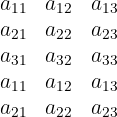
Schritt 2: Ermittle die positiven Summanden. Diese sind gegeben durch:
Das Produkt der Elemente auf der Hauptdiagonalen der Matrix
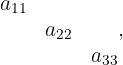
das Produkt der Elemente auf der Diagonalen, das unterhalb der Hauptdiagonalen der
Matrix liegt
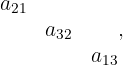
und das Produkt der Elemente in der nächsten Diagonale unterhalb der vorherigen Diagonalen.
Schritt 3. Ermittle die negativen Summanden. Diese sind das Produkt der Elemente in der sekundären Diagonalen der Matrix.
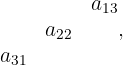
das Produkt der Elemente auf der Diagonalen, die unterhalb der sekundären Diagonalen liegt
de la matriz.
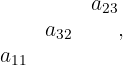
und das Produkt der Elemente in der nächsten Diagonalen unterhalb der vorherigen Diagonalen.
Schritt 4. Addiere die positiven Terme und die negativen Terme, die wir in den vorherigen Schritten ermittelt haben. Dies ergibt die gesuchte Determinante: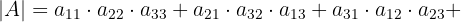 
Anwendungen
Matrizen der Dimension gehören zu den gängigsten in der linearen Algebra und die Berechnung ihrer Determinante ist von großer Bedeutung. Im Allgemeinen gibt es Systeme mit drei Gleichungen und drei Unbekannten. Eine Möglichkeit, um herauszufinden, ob ein solches System eine einzige Lösung hat oder nicht, besteht darin, die Determinante der zugehörigen Matrix zu berechnen. Hier erweist sich die Regel von Sarrus aufgrund ihrer Einfachheit und Effektivität als sehr nützlich.
Beispiele
1 Berechne die Determinante der folgenden Matrix
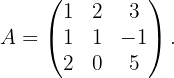
Die Diagonalen, die uns positive Terme liefern, sind die folgenden
Und die Diagonalen, die uns negative Terme liefern, sind die folgenden
Unter Verwendung der Regel von Sarrus erhalten wir schließlich
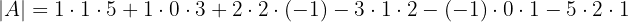
2 Argumentiere, ob die folgende Matrix invertierbar ist oder nicht.
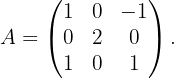
Eine Matrix ist genau dann invertierbar, wenn ihre Determinante ungleich 0 ist. Daher müssen wir die Determinante von 
berechnen. Die Diagonalen, die uns positive Terme liefern, sind die folgenden
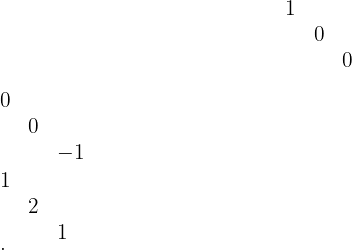
Und die Diagonalen, die uns negative Terme liefern, sind die folgenden
Unter Verwendung der Regel von Sarrus erhalten wir schließlich
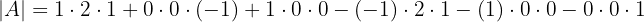
Wir kommen daher zu dem Schluss, dass die Matrix invertierbar ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
