Wurzeln mit gleichem Wurzelexponenten dividieren
Um Wurzeln mit dem gleichen Wurzelexponenten zu dividieren, werden die Radikanden dividiert und der gleiche Wurzelexponent beibehalten.
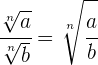
Beispiel: Dividiere die Wurzeln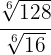 
1 Da die beiden Wurzeln den gleichen Wurzelexponenten haben, schreiben wir alles unter eine Wurzel mit dem gleichen Wurzelexponenten
2 Wir faktorisieren und dividieren die Potenzen mit gleicher Basis
3 Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und den Exponenten des Radikanden durch 
dividieren
Division von Wurzeln mit unterschiedlichem Wurzelexponenten
Zuerst werden sie auf einen gemeinsamen Wurzelexponenten gebracht, dann werden die Radikanden dividiert und der Wurzelexponent beibehalten.
Beispiel: Dividiere die Wurzeln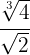 
1 Der gemeinsame Wurzelexponent ist das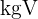 
der Wurzelexponenten
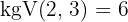
2 Wir dividieren den gemeinsamen Wurzelexponenten 
durch jeden der Wurzelexponenten und jedes Ergebnis wird mit den entsprechenden Exponenten multipliziert
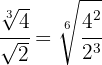
3 Wir zerlegen die 
in Faktoren und führen die entsprechenden Berechnungen mit den Potenzen durch
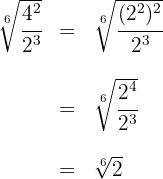
4 Wenn wir mit einer Rechenoperation fertig sind, vereinfachen wir die Wurzel, sofern möglich.
Beispiel: Dividiere die Wurzeln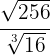 
1 Der gemeinsame Wurzelexponent ist das 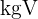der Wurzelexponenten
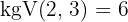
2 Wir dividieren den gemeinsamen Wurzelexponenten durch jeden der Wurzelexponenten und jedes Ergebnis wird mit den entsprechenden Exponenten multipliziert
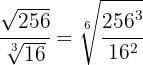
3 Wir zerlegen 
und 
in Faktoren und führen die entsprechenden Berechnungen mit den Potenzen durch
4 Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und den Exponenten des Radikanden durch 2 dividieren und schließlich Faktoren herausnehmen
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Im Rahmen einer Internetrecherche zu mathematischen Themen bin ich zufällig auf diese Seite gestoßen.Hier fielen mir Unstimmigkeiten auf: bei den ersten vier Beispielen liegen offensichtlich Formatierungsfehler vor, die sehen nämlich so aus:
„5-3∈ℕ3-5∉ℕ“, „6÷2∈ℕ2÷6∉ℕ“ „6÷2∈ℤ2÷6∉ℤ“ und „(-2)³=-8∈ℤ(-2)⁻³=-⅛∉ℤ“
das kann niemand lesen. Vermutlich fehlt jeweils ein Zeilenvorschub. Oder man schreibt was dazwischen, z.B. ein „aber“:
„5-3∈ℕ aber: 3-5∉ℕ“, „6÷2∈ℕ aber: 2÷6∉ℕ“ „6÷2∈ℤ aber: 2÷6∉ℤ“ und „(-2)³=-8∈ℤ aber: (-2)⁻³=-⅛∉ℤ“
So wäre es verständlich.
Jetzt aber zur Hauptsache: eigentlich ist alles ordentlich und korrekt erklärt. Nur, bei „rationale Zahlen“ steht da:
„““Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.“““
völlig korrekt, aber im Abschnitt danach:
„““Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen …“““
Das passt nicht zusammen, und der Sinn des Begriffs „irrationale Zahl“ bleibt unverständlich. Ja, im formallogischen Sinn kann man sagen „Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann“ – nur wirkt das wie „von hinten durch die Brust ins Auge“. Ich empfehle doch sehr, diesen Satz zu ändern in „Eine irrationale Zahl ist eine Zahl, die sich nicht als Quotient zweier ganzer Zahlen darstellen lässt. Ihre Dezimaldarstellung hat daher unendlich viele nichtperiodische Nachkommastellen“ Dann harmoniert das auch mit dem Abschnitt davor:
Rationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.
Irrationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen darstellen lässt.
Vielen Dank für die Hinweise. Wir haben die Vorschläge gerne angenommen und im Artikel aktualisiert.