Kapitel
- Bestandteile einer Wurzel
- Potenzen und Wurzeln
- Gleiche Wurzeln
- Vereinfachung von Wurzeln
- Gemeinsamer Wurzelexponent
- Teilweises Wurzelziehen
- Faktoren unter die Wurzel bringen
- Addition und Subtraktion von Wurzeln
- Multiplikation von Wurzeln mit dem gleichen Wurzelexponenten
- Multiplikation von Wurzeln mit unterschiedlichem Wurzelexponenten
- Wurzeln mit gleichem Wurzelexponenten dividieren
- Wurzeln mit unterschiedlichem Wurzelexponenten dividieren
- Potenz einer Wurzel
- Wurzel aus einer Wurzel
- Rationalisieren
Eine Wurzel ist ein Ausdruck der Form  , bei dem
, bei dem  und
und  . Wenn
. Wenn  außerdem eine gerade Zahl ist, kann
außerdem eine gerade Zahl ist, kann  nicht negativ sein
nicht negativ sein  .
.
Die Zahl  ist zum Beispiel eine gerade Zahl. Deshalb ist
ist zum Beispiel eine gerade Zahl. Deshalb ist 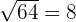 ; während
; während  .
.
Und da die Zahl  ungerade ist, ist
ungerade ist, ist  und
und 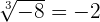 . Das heißt, die Kubikwurzel ist für jede reelle Zahl definiert.
. Das heißt, die Kubikwurzel ist für jede reelle Zahl definiert.

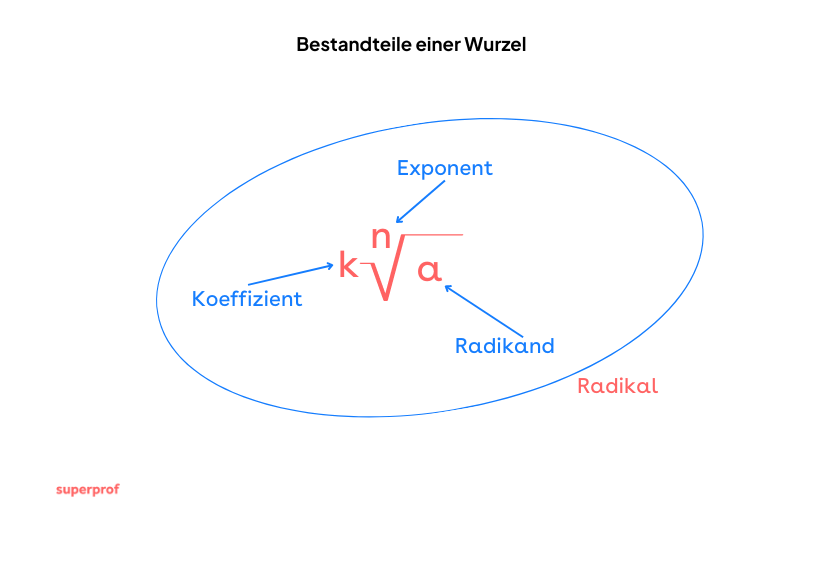
Bestandteile einer Wurzel
Potenzen und Wurzeln
Eine Wurzel kann als Potenz ausgedrückt werden:
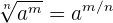
Beispiel:
Wir schreiben die Zahl  als Potenz:
als Potenz: 
Der Wurzelexponent der Wurzel  wird zum Nenner und der Exponent des Radikanden
wird zum Nenner und der Exponent des Radikanden 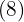 wird zum Zähler. Wir berechnen:
wird zum Zähler. Wir berechnen:
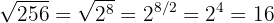
Gleiche Wurzeln
Unter Verwendung der Exponentenschreibweise für Brüche und der Eigenschaft von Brüchen, die besagt, dass der Bruch äquivalent ist, wenn Zähler und Nenner mit der gleichen Zahl multipliziert werden, gilt:
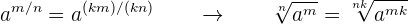
Multipliziert oder dividiert man den Wurzelexponenten und den/die Exponenten des Radikanden durch dieselbe natürliche Zahl, so erhält man eine weitere gleiche Wurzel.
Beispiel
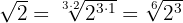
Vereinfachung von Wurzeln
Wenn es eine natürliche Zahl gibt, durch die der Wurzelexponent und der Exponent (oder die Exponenten) des Radikanden dividiert werden können, erhält man eine vereinfachte Wurzel.
Beispiele
1 Vereinfache 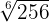
Wir schreiben  als Potenz:
als Potenz: 
Um die Wurzel zu vereinfachen, dividieren wir sowohl den Wurzelexponenten  als auch den Exponenten des Radikanden
als auch den Exponenten des Radikanden 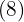 durch
durch 
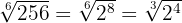
2 Vereinfache 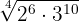
Um die Wurzel zu vereinfachen, dividieren wir sowohl den Wurzelexponenten  als auch die Exponenten des Radikanden
als auch die Exponenten des Radikanden 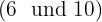 durch
durch 
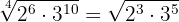
Gemeinsamer Wurzelexponent
Um zwei oder mehr Wurzeln auf einen gemeinamen Wurzelexponenten zu bringen, sind folgende Schritte nötig:
1 Wir ermitteln das kleinste gemeinsame Vielfache, das dann der gemeinsame Wurzelexponent ist
2 Wir dividieren das kleinste gemeinsame Vielfache durch jeden der Wurzelexponenten und multiplizieren jedes Ergebnis mit den entsprechenden Exponenten
Beispiel:
Wir ermitteln den gemeinsamen Wurzelexponenten:

Als Erstes bestimmen wir das kgV der Wurzelexponenten: 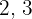 und
und 
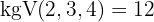
Wir dividieren den gemeinsamen Wurzelexponenten  durch jeden der Wurzelexponenten
durch jeden der Wurzelexponenten 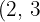 und
und 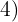 und multiplizieren jedes Ergebnis mit den entsprechenden Exponenten
und multiplizieren jedes Ergebnis mit den entsprechenden Exponenten

Wir rechnen mit den Potenzen

Teilweises Wurzelziehen
Um Faktoren aus einer Wurzel zu extrahieren, wird der Radikand in Faktoren zerlegt. Wenn:
Ein Exponent des Radikanden ist kleiner als der Wurzelexponent
Der entsprechende Faktor bleibt unter dem Radikanden.
Beispiele:
1 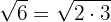
2 
Ein Exponent des Radikanden ist gleich dem Wurzelexponenten
Der entsprechende Faktor verlässt den Radikanden.
Beispiele:
1 
Wir zerlegen die Zahl  in Faktoren. Da die
in Faktoren. Da die  in dieselbe Potenz wie der Wurzelexponent erhoben wird, können wir die
in dieselbe Potenz wie der Wurzelexponent erhoben wird, können wir die  aus dem Radikanden extrahieren
aus dem Radikanden extrahieren
2 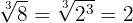
Wir zerlegen die Zahl  in Faktoren. Da die
in Faktoren. Da die  in dieselbe Potenz wie der Wurzelexponent erhoben wird, können wir die
in dieselbe Potenz wie der Wurzelexponent erhoben wird, können wir die  aus dem Radikanden extrahieren
aus dem Radikanden extrahieren
Ein Exponent des Radikanden ist größer als der Wurzelexponent
Dieser Exponent wird durch den Wurzelexponenten geteilt. Der erhaltene Quotient ist der Exponent des Faktors außerhalb des Radikanden und der Rest ist der Exponent des Faktors innerhalb des Radikanden
Beispiele:
1 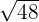
Der Exponent von 2 ist größer als der Wurzelexponent. Dieser Exponent  wird also durch den Wurzelexponenten
wird also durch den Wurzelexponenten  dividiert
dividiert
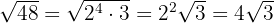
Der erhaltene Quotient  ist der Exponent des Faktors außerhalb des Radikanden und der Rest
ist der Exponent des Faktors außerhalb des Radikanden und der Rest 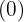 ist der Exponent des Faktors innerhalb des Radikanden.
ist der Exponent des Faktors innerhalb des Radikanden.
Da der Faktor  gleich 1 ist, muss er nicht in den Radikanden gebracht werden, da er sich nicht ändert, wenn er mit einem anderen Faktor multipliziert wird.
gleich 1 ist, muss er nicht in den Radikanden gebracht werden, da er sich nicht ändert, wenn er mit einem anderen Faktor multipliziert wird.
Im Allgemeinen gilt: Wenn das Ergebnis der Division des Exponenten eines Faktors durch den Wurzelexponenten null ergibt, wird dieser Faktor nicht in den Radikanden gebracht
2 
Wir zerlegen in Faktoren: 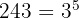
Der Exponent ist größer als der Wurzelexponent. Also wird dieser Exponent  durch den Wurzelexponenten
durch den Wurzelexponenten 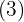 dividiert.
dividiert.
Der erhaltene Quotient  ist der Exponent des Faktors außerhalb des Radikanden und der Rest
ist der Exponent des Faktors außerhalb des Radikanden und der Rest  ist der Exponent innerhalb des Radikanden.
ist der Exponent innerhalb des Radikanden.

3 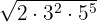
Es gibt Exponenten im Radikanden, die größer als der Wurzelexponent sind. Somit werden diese Exponenten 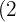 und
und 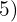 durch den Wurzelexponenten
durch den Wurzelexponenten  dividiert.
dividiert.
Jeder der erhaltenen Quotienten  und
und  ist dann der Exponent des entsprechendenen Faktors außerhalb des Radikanden und die erhaltenen Reste
ist dann der Exponent des entsprechendenen Faktors außerhalb des Radikanden und die erhaltenen Reste  und
und  sind dann die Exponenten der entsprechenden Faktoren innerhalb des Radikanden
sind dann die Exponenten der entsprechenden Faktoren innerhalb des Radikanden

4 
Die Exponenten des Radikanden sind größer als der Wurzelexponent. Also werden diese Exponenten  und
und 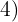 durch den Wurzelexponenten
durch den Wurzelexponenten  dividiert.
dividiert.
Jeder der Quotienten 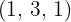 ist dann der entsprechende Faktor außerhalb des Radikanden und die erhaltenen Reste
ist dann der entsprechende Faktor außerhalb des Radikanden und die erhaltenen Reste 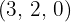 sind dann die Exponenten der entsprechenden Faktoren innerhalb des Radikanden
sind dann die Exponenten der entsprechenden Faktoren innerhalb des Radikanden
Faktoren unter die Wurzel bringen
Um Faktoren unter eine Wurzel zu bringen, müssen die Faktoren hoch den Wurzelexponenten der Wurzel genommen werden
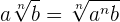
Beispiele:
1 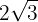
Da der Wurzelexponent  ist, wird der Faktor außerhalb der Wurzel
ist, wird der Faktor außerhalb der Wurzel  quadriert und wir berchnen
quadriert und wir berchnen
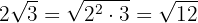
2 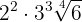
Sowohl  als auch
als auch  werden hoch vier genommen:
werden hoch vier genommen:
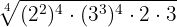
Wir lösen die Klammern auf, indem wir die Exponenten multiplizieren

Wir multiplizieren die Potenzen mit der gleichen Basis
Addition und Subtraktion von Wurzeln
Zwei Wurzeln können nur addiert (oder subtrahiert) werden, wenn die Wurzeln gleich sind. Das heißt, dass es sich um Wurzeln handeln muss, die den gleichen Wurzelexponenten und Radikanden haben.
Um Wurzeln mit dem gleichen Wurzelexponenten und Radikanden zu addieren/subtrahieren, werden die Koeffizienten der Wurzeln addiert/subtrahiert.

Beispiele:
1 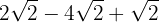
Wir fassen die Koeffizienten der Wurzeln zusammen
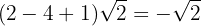
2 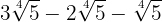
Wir fassen die Koeffizienten der Wurzeln zusammen
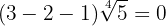
3 
Wir zerlegen die Radikanden in Faktoren:

Die Wurzeln sind also
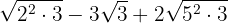
Wir extrahieren die Faktoren aus den Wurzeln und multiplizieren sie mit dem Koeffizienten der entsprechenden Wurzel
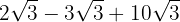
Wir fassen die Koeffizienten der Wurzeln zusammen
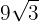
4 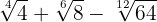
Wir extrahieren die Faktoren aus den Wurzeln und multiplizieren sie mit dem Koeffizienten der entsprechenden Wurzel
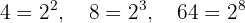
Somit
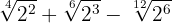
Wir vereinfachen die Wurzeln. Bei der ersten Wurzel dividieren wir den Wurzelexponenten und den Exponenten des Radikanden durch  , bei der zweiten Wurzel durch
, bei der zweiten Wurzel durch  und bei der dritten Wurzel durch
und bei der dritten Wurzel durch 
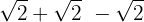
Wir fassen die Koeffizienten der Wurzeln zusammen
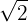
Beispielaufgaben zur Addition und Subtraktion von Wurzeln
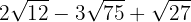
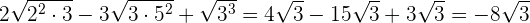
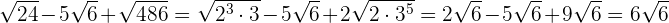
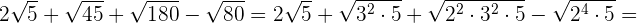
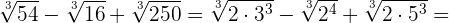
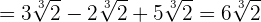
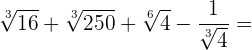
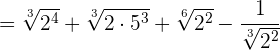
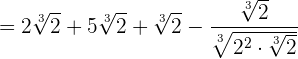
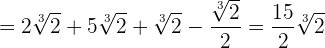
Multiplikation von Wurzeln mit dem gleichen Wurzelexponenten
Um Wurzeln mit dem gleichen Wurzelexponenten zu multiplizieren, werden die Radikanden multipliziert und der Wurzelexponent bleibt gleich.

Beispiel:
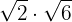
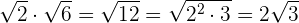
Sobald wir einen Rechenschritt durchgeführt haben, ziehen wir, wenn möglich, Faktoren aus der Wurzel.
Multiplikation von Wurzeln mit unterschiedlichem Wurzelexponenten
Zunächst müssen sie auf einen gemeinamen Wurzelexponenten gebracht werden, danach werden sie multipliziert.
Beispiele:
1 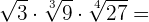
Wir zerlegen die Radikanden in Faktoren

Wir bringen auf einen gemeinsamen Wurzelexponenten und müssen also das kleinste gemeinsame Vielfache der Wurzelexponenten berechnen. Dies ist dann der gemeinsame Wurzelexponent.
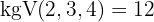
Wir dividieren den gemeinsamen Wurzelexponenten  durch jeden der Wurzelexponenten
durch jeden der Wurzelexponenten 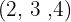 und jedes erhaltene Ergebnis multiplizieren wir mit den entsprechenden Exponenten
und jedes erhaltene Ergebnis multiplizieren wir mit den entsprechenden Exponenten  . Wir führen das Produkt der Potenzen mit der gleichen Basis im Radikanden aus und extrahieren Faktoren aus dem Radikanden
. Wir führen das Produkt der Potenzen mit der gleichen Basis im Radikanden aus und extrahieren Faktoren aus dem Radikanden

2 
Wir berechnen das kleinste gemeinsame Vielfache der Wurzelexponenten
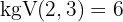
Wir dividieren den gemeinsamen Wurzelexponenten  durch jeden der Wurzelexponenten
durch jeden der Wurzelexponenten 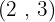 und nehmen jedes Ergebnis hoch den entsprechenden Radikanden
und nehmen jedes Ergebnis hoch den entsprechenden Radikanden
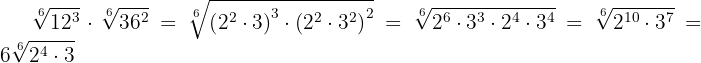
Wir zerlegen  und
und  in Faktoren, führen die notwendigen Rechenschritte durch und extrahieren Faktoren
in Faktoren, führen die notwendigen Rechenschritte durch und extrahieren Faktoren
Wurzeln mit gleichem Wurzelexponenten dividieren
Um Wurzeln mit gleichem Wurzelexponenten zu dividieren, werden die Radikanden dividiert und der Wurzelexponent bleibt gleich.
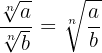
Beispiel:
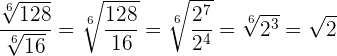
Da die Wurzeln den gleichen Wurzelexponenten haben, können wir alles unter eine Wurzel schreiben
Wir faktorisieren und dividieren die Potenzen mit der gleichen Basis
Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und den Radikanden durch dividieren
dividieren
Wurzeln mit unterschiedlichem Wurzelexponenten dividieren
Als Erstes bringen wir auf einen gemeinsamen Wurzelexponenten, danach dividieren wir.
Beispiele:
1 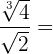
Zunächst bringen wir auf einen gemeinsamen Wurzelexponenten. Also müssen wir das kleinste gemeinsame Vielfache der Wurzelexponenten berechnen, das dann der gemeinsame Wurzelexponent ist. 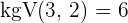 .
.
Wir dividieren den gemeinsamen Wurzelexponenten  durch jeden der Wurzelexponenten (
durch jeden der Wurzelexponenten ( und
und  ) und multiplizieren jedes Ergebnis mit den entsprechenden Exponenten (
) und multiplizieren jedes Ergebnis mit den entsprechenden Exponenten ( und
und  )
)
Wir zerlegen die  in Faktoren, um die Division wie folgt durchführen zu können
in Faktoren, um die Division wie folgt durchführen zu können
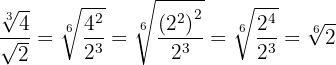
2 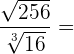
Wir führen dieselben Schritte wie beim vorhergehenden Beispiel durch

Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und den Exponenten des Radikanden durch  dividieren und extrahieren schließlich Faktoren
dividieren und extrahieren schließlich Faktoren
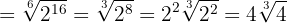
Potenz einer Wurzel
Um eine Wurzel mit einem Exponenten zu potenzieren, wird der Radikand mit dem Exponenten potenziert. Der Wurzelexponent bleicht gleich.
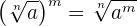
Beispiel:
1 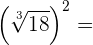
Wir quadrieren den Radikanden, zerlegen die  in Faktoren und quadrieren. Und schließlich schreiben wir den Faktor vor die Wurzel
in Faktoren und quadrieren. Und schließlich schreiben wir den Faktor vor die Wurzel
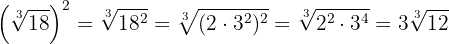
2 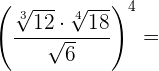
Wir nehmen die Radikanden hoch vier, zerlegen sie in Faktoren und extrahieren die  aus der Wurzel
aus der Wurzel
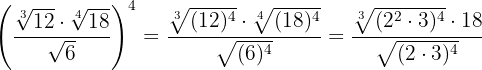
Wir führen bei den Radikanden die nötigen Rechenschritte zum Rechnen mit Potenzen durch und ermitteln den gemeinsamen Wurzelexponenten, um dividieren zu können
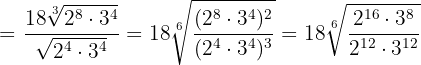
Wir vereinfachen die Wurzel, indem wir den Wurzelexponenten und die Exponenten des Radikanden durch  dividieren und führen eine Division von Potenzen mit dem gleichen Exponenten durch
dividieren und führen eine Division von Potenzen mit dem gleichen Exponenten durch
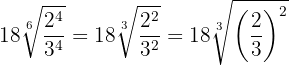
3 Schreibe folgende Potenzen als Wurzeln:
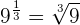
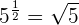
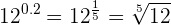
4 Schreibe als Potenz mit rationalem Exponenten
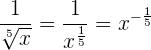
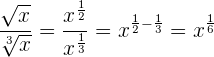
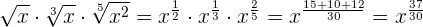
Wurzel aus einer Wurzel
Die Wurzel aus einer Wurzel ist eine andere Wurzel mit dem gleichen Radikanden, deren Wurzelexponent das Produkt aus den beiden Wurzelexponenten ist.
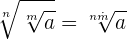
Beispiel:
1 
Wir multiplizieren die Wurzelexponenten
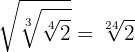
2 
Wir bringen die erste  unter die Kubikwurzel. Dazu müssen wir sie hoch drei nehmen und die Potenzen mit der gleichen Basis multiplizieren
unter die Kubikwurzel. Dazu müssen wir sie hoch drei nehmen und die Potenzen mit der gleichen Basis multiplizieren
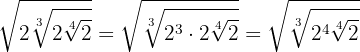
Wir bringen die  unter die vierte Wurzel. Also müssen wir sie hoch vier nehmen, die Potenzen multiplizieren und schließlich die Wurzelexponenten multiplizieren
unter die vierte Wurzel. Also müssen wir sie hoch vier nehmen, die Potenzen multiplizieren und schließlich die Wurzelexponenten multiplizieren

Rationalisieren
Beim Rationalisieren einer Wurzel müssen die Wurzeln aus dem Nenner eliminiert werden. Dies erleichtert zum Beispiel die Addition von Brüchen
Es gibt drei unterschiedliche Fälle:
Fall 1
Rationalisierung vom Typ 
Zähler und Nenner werden mit  multipliziert
multipliziert

Beispiele:
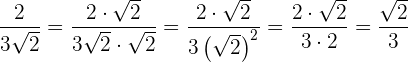
Fall 2
Rationalisierung vom Typ 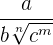
Zähler und Nenner werden mit 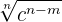 multipliziert
multipliziert

Beispiel:

Wir schreiben den Radikanden  als Potenz:
als Potenz: 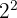
Wir müssen den Zähler und den Nenner mit der fünften Wurzel aus 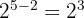 multiplizieren
multiplizieren
Wir multiplizieren die Wurzeln des Nenners, extrahieren Faktoren aus der Wurzel und vereinfachen den Bruch
Fall 3
Rationalisierung vom Typ 
Und im Allgemeinen, wenn der Nenner ein Binom mit mindestens einer Wurzel ist.
Der Bruch wird mit dem Term, der im Nenner steht, erweitert.
Das konjugierte Binom ist immer gleich dem Binom mit umgekehrtem Vorzeichen:
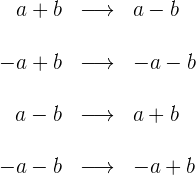
Außerdem müsssen wir bedenken: "Summe mal Differenz ist gleich Differenz zum Quadrat".

Beispiele:
1 
Wir multiplizieren den Zähler und den Nenner mit dem Konjugierten des Nenners, lösen die Klammer im Zähler auf und rechnen Summe mal Differenz im Nenner. So erhalten wir eine Differenz zum Quadrat
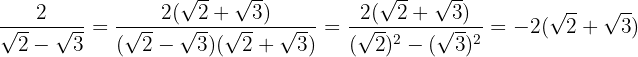
2 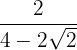
Wir erweitern den Bruch mit dem Konjugierten des Nenners
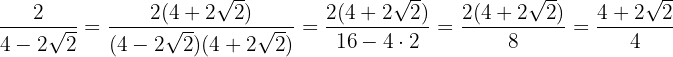
3 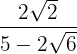
Wir multiplizieren den Zähler und den Nenner mit dem Konjugierten des Nenners, lösen die Klammer im Zähler auf und rechnen Summe mal Differenz im Nenner. So erhalten wir eine Differenz zum Quadrat
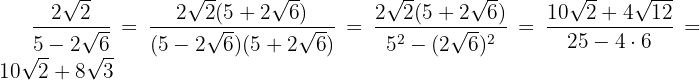
Mit KI zusammenfassen:













