Kapitel

Wie berechnen wir die Fläche zwischen zwei Funktionen?
Die Fläche zwischen zwei Funktionen ist gleich der Fläche der oberen Funktion minus der Fläche der unteren Funktion.
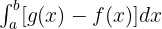
Beispiel mit Lösung der Fläche zwischen zwei Funktionen
Berechne die durch den Graphen
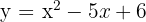
und die Gerade
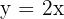 begrenzte Fläche.
begrenzte Fläche.
Zunächst ermitteln wir die Schnittpunkte der beiden Funktionen, um die Integrationsgrenzen zu kennen.
Dazu lösen wir die folgende Gleichung
 ,
,
das heißt, wir setzen die Funktionen gleich.
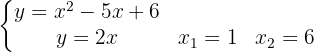
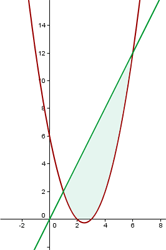
Von  bis
bis  verläuft die Gerade oberhalb der Parabel. Somit ist die Fläche gegeben durch:
verläuft die Gerade oberhalb der Parabel. Somit ist die Fläche gegeben durch:
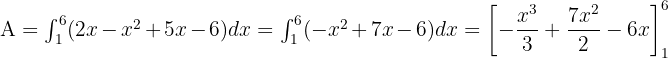
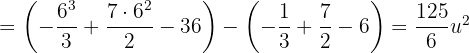
Aufgaben zur Fläche zwischen zwei Funktionen
Berechne die durch die Parabel 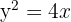 und die Gerade
und die Gerade 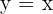 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
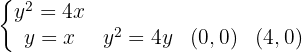
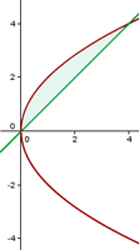
Von  bis
bis  vereläuft die Parabel oberhalb der Geraden.
vereläuft die Parabel oberhalb der Geraden.
Somit ist die Fläche gegeben durch:
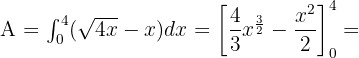
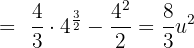
Berechne die durch die Parabel  und die Gerade
und die Gerade 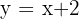 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
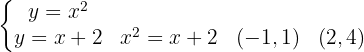
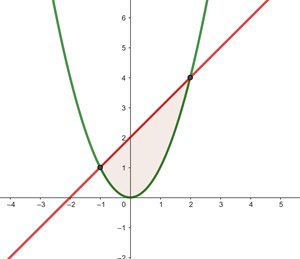
Von  bis
bis  verläuft die Gerade oberhalb der Parabel.
verläuft die Gerade oberhalb der Parabel.
Somit ist die Fläche gegeben durch:
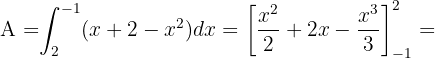
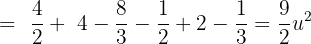
Berechne die Fläche, die durch die Parabel  und die Gerade
und die Gerade 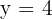 begrenzt ist
begrenzt ist
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
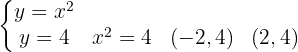
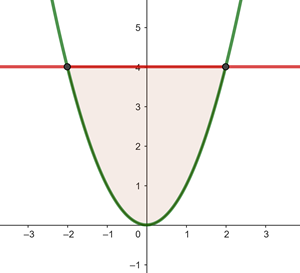
Von  bis
bis  verläuft die Gerade oberhalb der Parabel.
verläuft die Gerade oberhalb der Parabel.
Somit ist die Fläche gegeben durch:
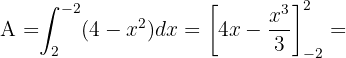
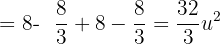
Berechne die durch die Parabeln  und
und 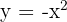 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
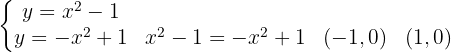
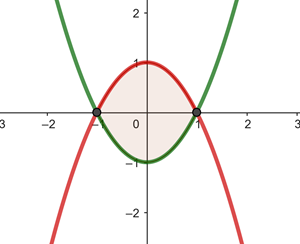
Von  bis
bis  verläuft die Parabel
verläuft die Parabel 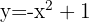 oberhalb der Parabel
oberhalb der Parabel 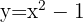 .
.
Somit ist die Fläche gegeben durch:
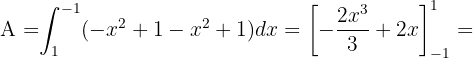
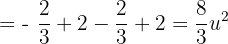
Berechne die durch die Graphen 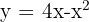 und
und 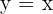 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
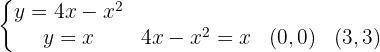
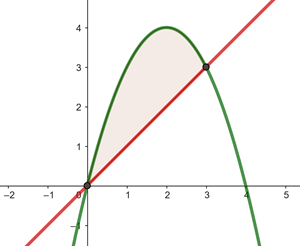
Von  bis
bis  verläuft die Parabel
verläuft die Parabel 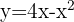 oberhalb der Geraden
oberhalb der Geraden  .
.
Somit ist die Fläche gegeben durch:
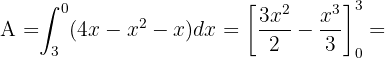
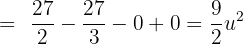
Berechne die durch die Parabel 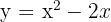 und die Gerade
und die Gerade 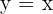 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
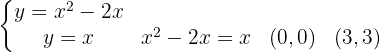
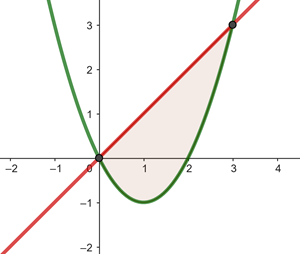
Von  bis
bis  verläuft die Parabel
verläuft die Parabel 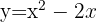 unterhalb der Geraden
unterhalb der Geraden  .
.
Somit ist die Fläche gegeben durch:
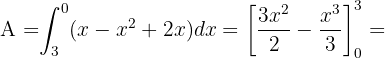
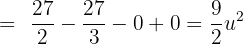
Berechne die durch die Parabel 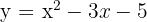 und die Gerade
und die Gerade 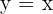 begrenzte Fläche
begrenzte Fläche
Wir beginnen mit der Ermittlung der Integrationsgrenzen durch Gleichsetzen der Funktionen:
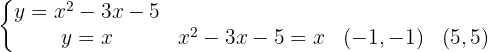
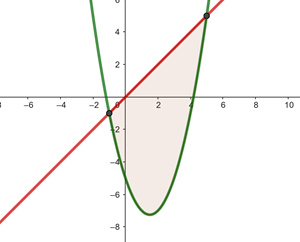
Von  bis
bis 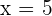 verläuft die Parabel
verläuft die Parabel 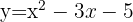 unterhalb der Geraden
unterhalb der Geraden  .
.
Somit ist die Fläche gegeben durch:
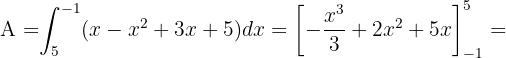
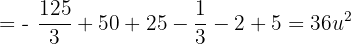
Berechne die Fläche, die durch die Graphen der Funktionen 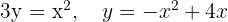 begrenzt ist.
begrenzt ist.
Zunächst stellen wir die Parabeln ausgehend vom Scheitelpunkt und den Schnittpunkten mit den Achsen dar.
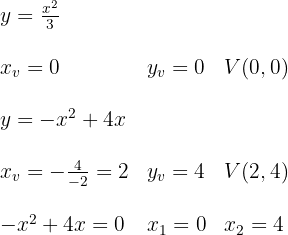
Wir ermitteln auch die Schnittpunkte der Funktionen, die uns die Integrationsgrenzen angeben.
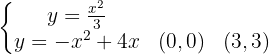
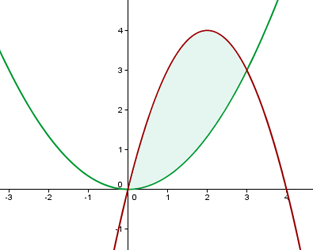
Von  bis
bis  verläuft die Parabel
verläuft die Parabel 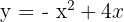 oberhalb der Parabel
oberhalb der Parabel 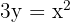 .
.
Somit ist die Fläche gegeben durch:
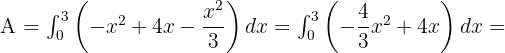
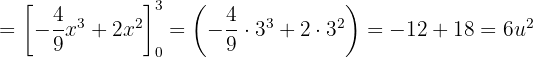
Ermittle die Fläche der Figur in der Ebene, die durch die Parabeln 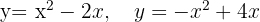 begrenzt ist.
begrenzt ist.
Wir stellen die Parabeln ausgehend vom Scheitelpunkt und den Schnittpunkten mit den Achsen dar.
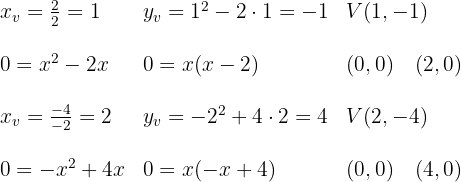
Wir ermitteln auch die Schnittpunkte der Funktionen, die uns die Integrationsgrenzen angeben.
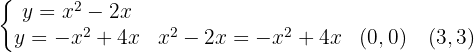
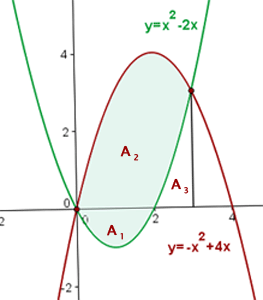
Von  bis
bis  befindet sich ein Teil der Fläche zwischen den Funktionen unterhalb der x-Achse.
befindet sich ein Teil der Fläche zwischen den Funktionen unterhalb der x-Achse.
Von  bis
bis  berechnen wir die Fläche unterhalb der Parabel
berechnen wir die Fläche unterhalb der Parabel  .
.
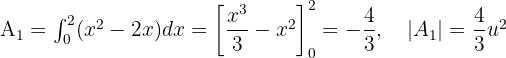
Von  bis
bis  berechnen wir die Fläche unterhalb der Parabel
berechnen wir die Fläche unterhalb der Parabel 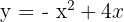 .
.
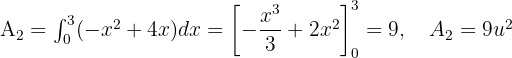
Von  bis
bis  haben wir einen Flächenüberschuss, der der Fläche unterhalb der Parabel
haben wir einen Flächenüberschuss, der der Fläche unterhalb der Parabel 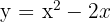 entspricht.
entspricht.

Schließlich führen wir die entsprechenden Berechnungen durch.
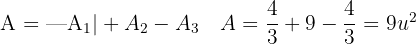
Ermittle den Flächeninhalt des Bereichs, der durch die Funktionen 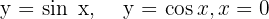 begrenzt ist.
begrenzt ist.
Zunächst ermitteln wir den Schnittpunkt der Funktionen:
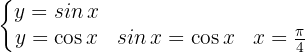
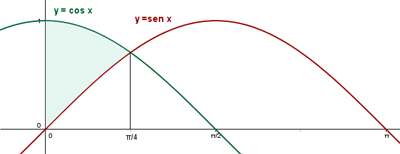
Der Kosinusgraph liegt auf dem Integrationsintervall oberhalb des Sinusgraphs..
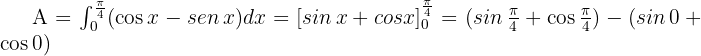

Mit KI zusammenfassen:












