Kapitel
Willkommen in unserem Bereich, der sich mit Übungen zum Thema Flächen und Funktionen befasst. Mathematische Funktionen sind wichtige Werkzeuge zur Beschreibung und Modellierung von Phänomenen in verschiedenen Disziplinen. In diesem Leitfaden führen wir dich durch Übungen zum Verständnis und zur Berechnung von Flächen unter Graphen, die durch Funktionen dargestellt werden.
Die Bestimmung der Fläche unter einem Funktionsgraphen erfordert die Anwendung von Konzepten der Integralrechnung. Diese Übungen werden nicht nur dein Verständnis für mathematische Funktionen stärken, sondern dir auch praktische Werkzeuge an die Hand geben, um reale Probleme zu lösen, die mit der Flächenberechnung zusammenhängen. Komm mit uns auf diese spannende mathematische Reise, auf der wir fortgeschrittene Konzepte anwenden werden, um Herausforderungen im Zusammenhang mit Funktionen und ihren Flächen zu bewältigen.

Aufgaben mit Lösungen
Berechne den Flächeninhalt der Fläche, die durch den Graphen von 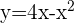 und die
und die 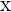 -Achse begrenzt ist.
-Achse begrenzt ist.
Berechne den Flächeninhalt der Fläche, die durch den Graphen von 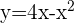 und die
und die 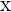 -Achse begrenzt ist.
-Achse begrenzt ist.
1 Zunächst ermitteln wir die Schnittpunkte mit der 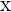 -Achse, um den Graphen darstellen zu können und die Integrationsgrenzen zu bestimmen.
-Achse, um den Graphen darstellen zu können und die Integrationsgrenzen zu bestimmen.
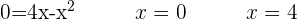
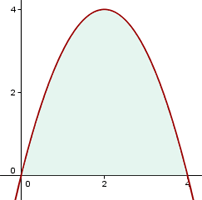
1 Anschließend wird das Integral berechnet:

Berechne die Fläche der Ebene, die durch den Schnittpunkt des Graphen 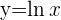 mit der
mit der 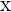 -Achse und dem Punkt
-Achse und dem Punkt 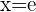 auf der x-Achse begrenzt ist.
auf der x-Achse begrenzt ist.
Berechne die Fläche der Ebene, die durch den Schnittpunkt des Graphen 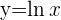 mit der
mit der 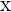 -Achse und dem Punkt
-Achse und dem Punkt 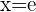 auf der x-Achse begrenzt ist.
auf der x-Achse begrenzt ist.
1 Als Erstes berechnen wir den Schnittpunkt mit der x-Achse.
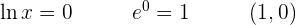
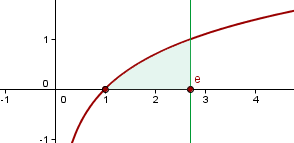

2 Das Integral wird mit der partiellen Integration gelöst
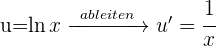
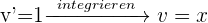
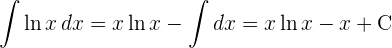

Berechne die Fläche, die durch die Gerade  , die
, die 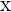 -Achse und die Ordinaten
-Achse und die Ordinaten 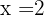 und
und 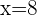 begrenzt ist.
begrenzt ist.
Berechne die Fläche, die durch die Gerade  , die
, die 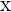 -Achse und die Ordinaten
-Achse und die Ordinaten 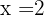 und
und 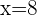 begrenzt ist.
begrenzt ist.
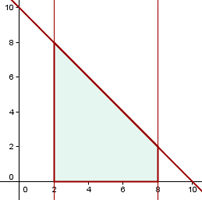
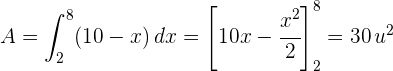
Berechne die Fläche, die durch den Graphen 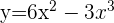 und die x-Achse begrenzt ist.
und die x-Achse begrenzt ist.
Berechne die Fläche, die durch den Graphen 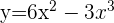 und die x-Achse begrenzt ist.
und die x-Achse begrenzt ist.
1 Wir berechnen die Schnittpunkte der Funktion mit der x-Achse

2 Wir stellen das Integral auf und lösen

Berechne die Fläche der Bereiche, die durch den Graphen 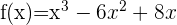 und die
und die 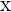 -Achse begrenzt sind.
-Achse begrenzt sind.
Berechne die Fläche der Bereiche, die durch den Graphen f(x) = x³ − 6x² + 8x und die x-Achse begrenzt sind.
1 Wir berechnen die Schnittpunkte der Funktion mit der x-Achse.

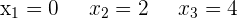
Berechne die Fläche des Kreises mit dem Radius  .
.
Berechne die Fläche des Kreises mit dem Radius 
1 Wir gehen von der Kreisgleichung aus und bestimmen 
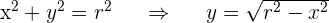
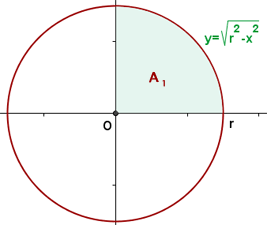
2 Die Fläche des Kreises ist viermal so groß wie die Fläche des 1. Quadranten, so dass
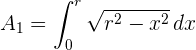
3 Wir berechnen das unbestimmte Integral durch Substitution.


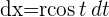

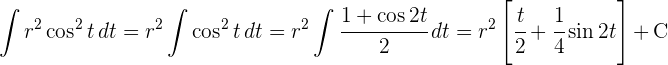
4 Wir bestimmen die neuen Integrationsgrenzen und substituieren
[


Bestimme den Flächeninhalt einer Ellipse mit den Halbachsen  und
und  .
.
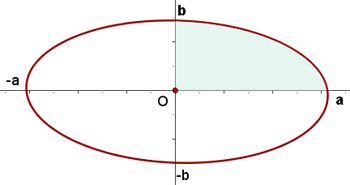
1 Wir gehen von der Ellipsengleichung aus

2 Da die Ellipse ein symmetrischer Graph ist, beträgt die geforderte Fläche das  -fache der vom 1. Quadranten und den Koordinatenachsen eingeschlossenen Fläche.
-fache der vom 1. Quadranten und den Koordinatenachsen eingeschlossenen Fläche.
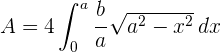
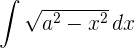
3 Wir lösen das Integral mit der Substitution
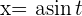
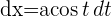


4 Wir ermitteln die neuen Integrationsgrenzen und substituieren

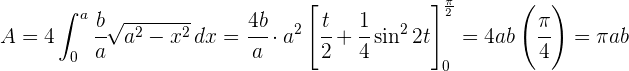
Wir berechnen die Fläche, die durch den Graphen  und die Gerade
und die Gerade  begrenzt ist.
begrenzt ist.
Berechne die Fläche, die durch den Graphen  und die Gerade
und die Gerade  begrenzt ist.
begrenzt ist.
1 Zunächst bestimmen wir die Schnittpunkte der beiden Funktionen, um die Integrationsgrenzen zu ermitteln.
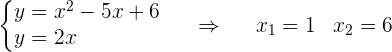
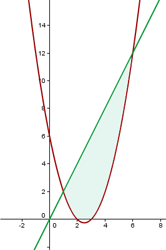
1 Von  bis
bis 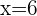 befindet sich die Gerade über der Parabel, sodass
befindet sich die Gerade über der Parabel, sodass
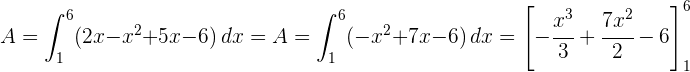
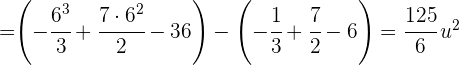
Berechne die Fläche, die durch die Parabel 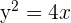 und die Gerade
und die Gerade  begrenzt ist.
begrenzt ist.
Berechne die Fläche, die durch die Parabel 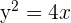 und die Gerade
und die Gerade  begrenzt ist.
begrenzt ist.
1 Wir berechnen die Schnittpunkte der Funktionen
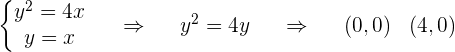
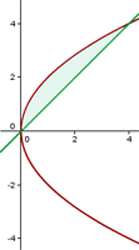
2 Von  bis
bis 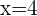 bleibt die Parabel über der Geraden, sodass
bleibt die Parabel über der Geraden, sodass

Berechne die Fläche, die von den Graphen der Funktionen  und
und 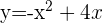 begrenzt wird.
begrenzt wird.
Berechne die Fläche, die von den Graphen der Funktionen  und
und 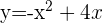 begrenzt wird.
begrenzt wird.
1 Zunächst stellen wir die Parabeln ausgehend vom Scheitelpunkt und den Schnittpunkten mit den Achsen dar.

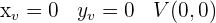
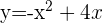
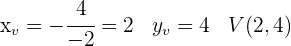
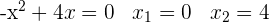
2 Außerdem ermitteln wir die Schnittpunkte der Funktionen, die uns die Integrationsgrenzen angeben.
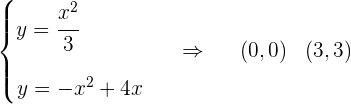
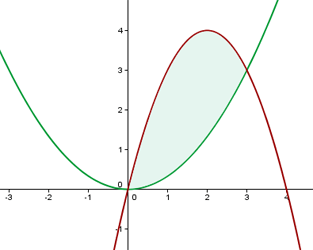

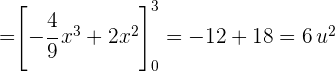
Berechne die Fläche, die durch die Parabeln 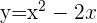 ,
, 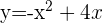 begrenzt wird.
begrenzt wird.
Berechne die Fläche, die durch die Parabeln 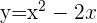 ,
, 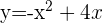 begrenzt wird.
begrenzt wird.
1 Wir stellen die Parabeln ausgehend vom Scheitelpunkt und den Schnittpunkten mit den Achsen dar.
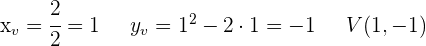

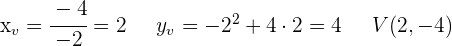
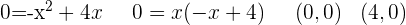

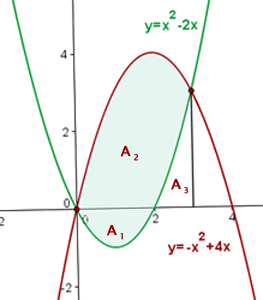
2 Wir betrachten die Flächen oberhalb und unterhalb der x-Achse, um die Gesamtfläche zu berechnen
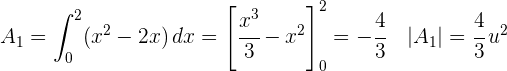


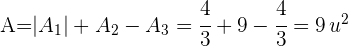
Bestimme die Fläche zwischen dem Graphen Kurve 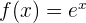 und dem Graphen
und dem Graphen 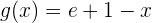 im Intervall
im Intervall 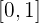 .
.
1
Zunächst analysieren wir den Schnittpunkt der beiden Graphen. Man beachte, dass für die Punkte 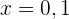 gilt
gilt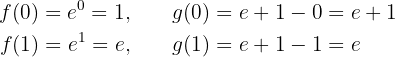
Dann ist die Funktion  im vorgeschlagenen Intervall immer größer als oder gleich
im vorgeschlagenen Intervall immer größer als oder gleich 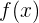 .
.
2
Nun berechnen wir das Integral von  im Intervall, um die Fläche zu ermitteln:
im Intervall, um die Fläche zu ermitteln: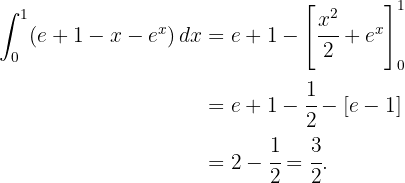
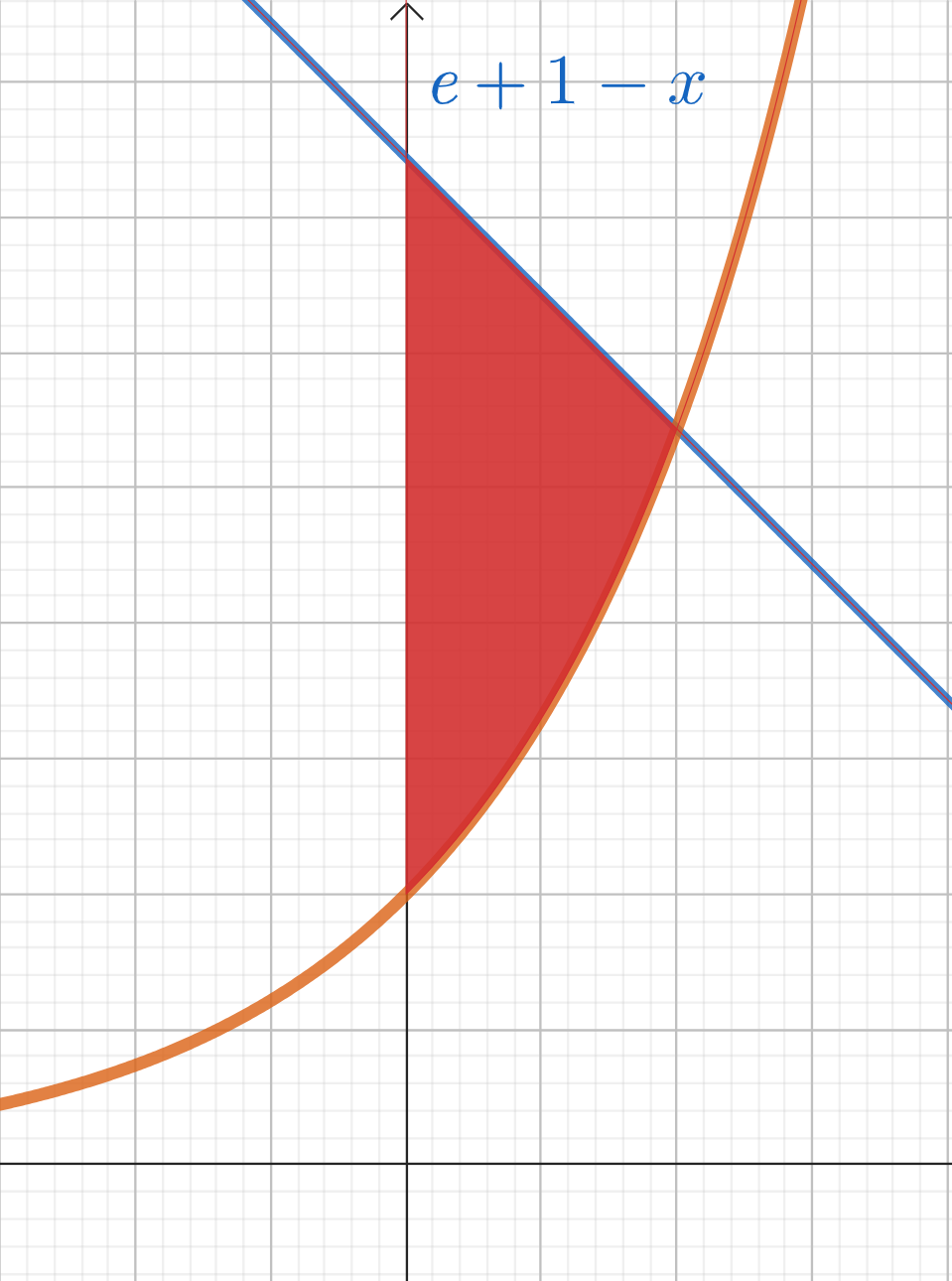
Ermittle die Fläche zwischen den Graphen 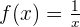 und
und  im Intervall
im Intervall 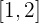 .
.
1
Zunächst analysieren wir die Schnittpunkte dieser Graphen. Beachte, dass für die Punkte 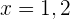 gilt
gilt
2
Nun berechnen wir das Integral von  im Intervall, um die Fläche zu ermitteln:
im Intervall, um die Fläche zu ermitteln: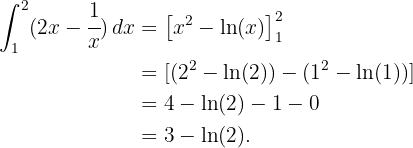
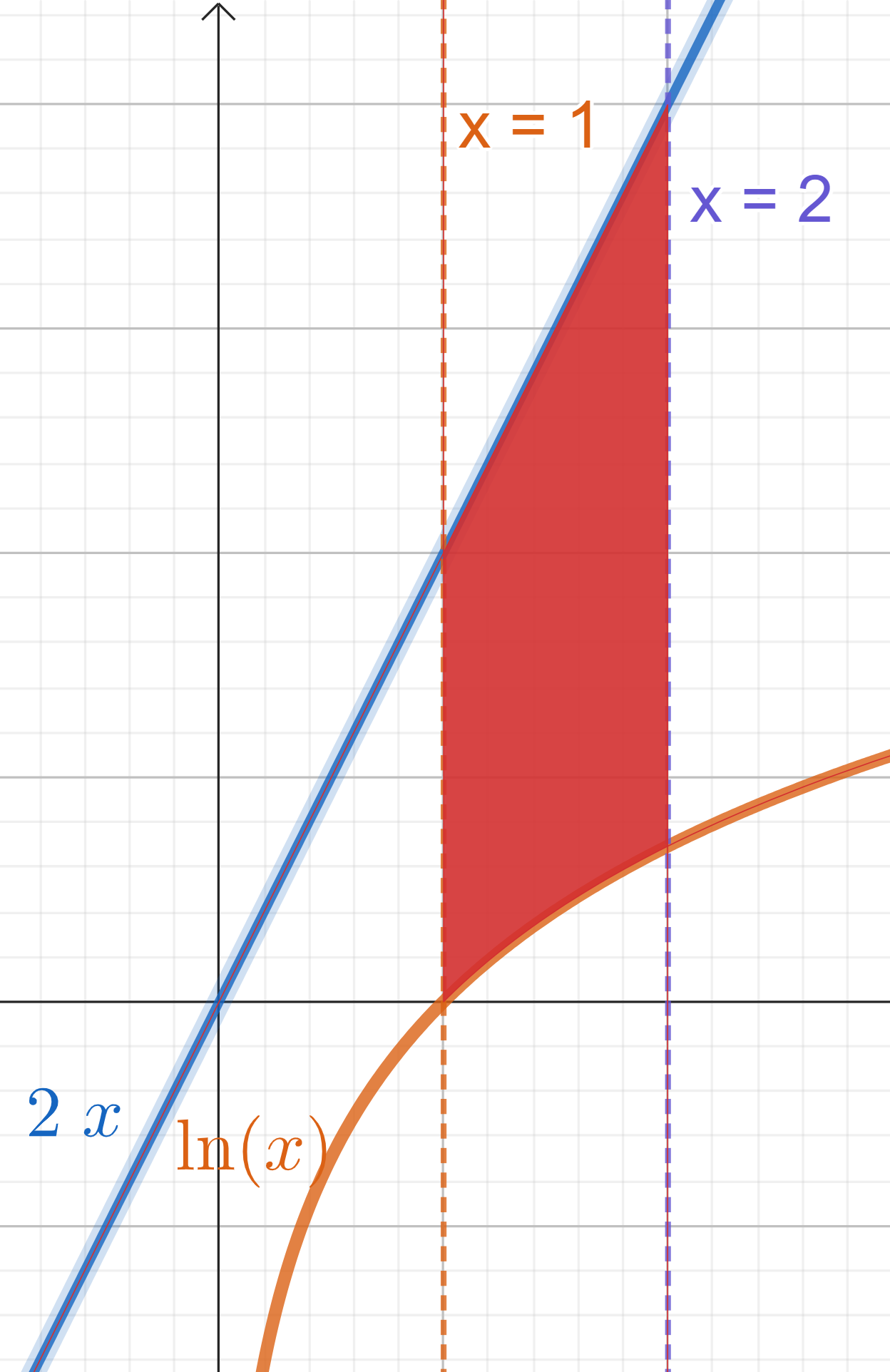
Bestimme die Fläche zwischen den Graphen 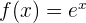 und
und  im Intervall
im Intervall 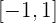 .
.
1
Zunächst analysieren wir die Schnittpunkte dieser Graphen. Beachte, dabeachte, dass für die Punkte  gilt
gilt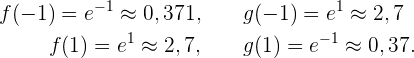
Einfach ausgedrückt, gilt 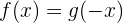 für alle
für alle 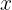 . Genauer gesagt,
. Genauer gesagt, 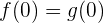 . Um die Fläche zu berechnen, müssen wir also das Integral an diesem Punkt abtrennen, an dem die Änderung der Hauptfunktion (diejenige mit dem größten Wert) zu finden ist.
. Um die Fläche zu berechnen, müssen wir also das Integral an diesem Punkt abtrennen, an dem die Änderung der Hauptfunktion (diejenige mit dem größten Wert) zu finden ist.
2
Wie wir oben festgestellt haben, ist  im Intervall
im Intervall 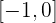 , aber dann ist
, aber dann ist  im Intervall
im Intervall  . Die Fläche zwischen den Graphen ist also
. Die Fläche zwischen den Graphen ist also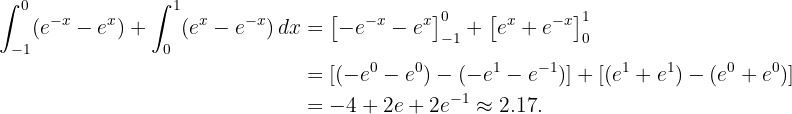
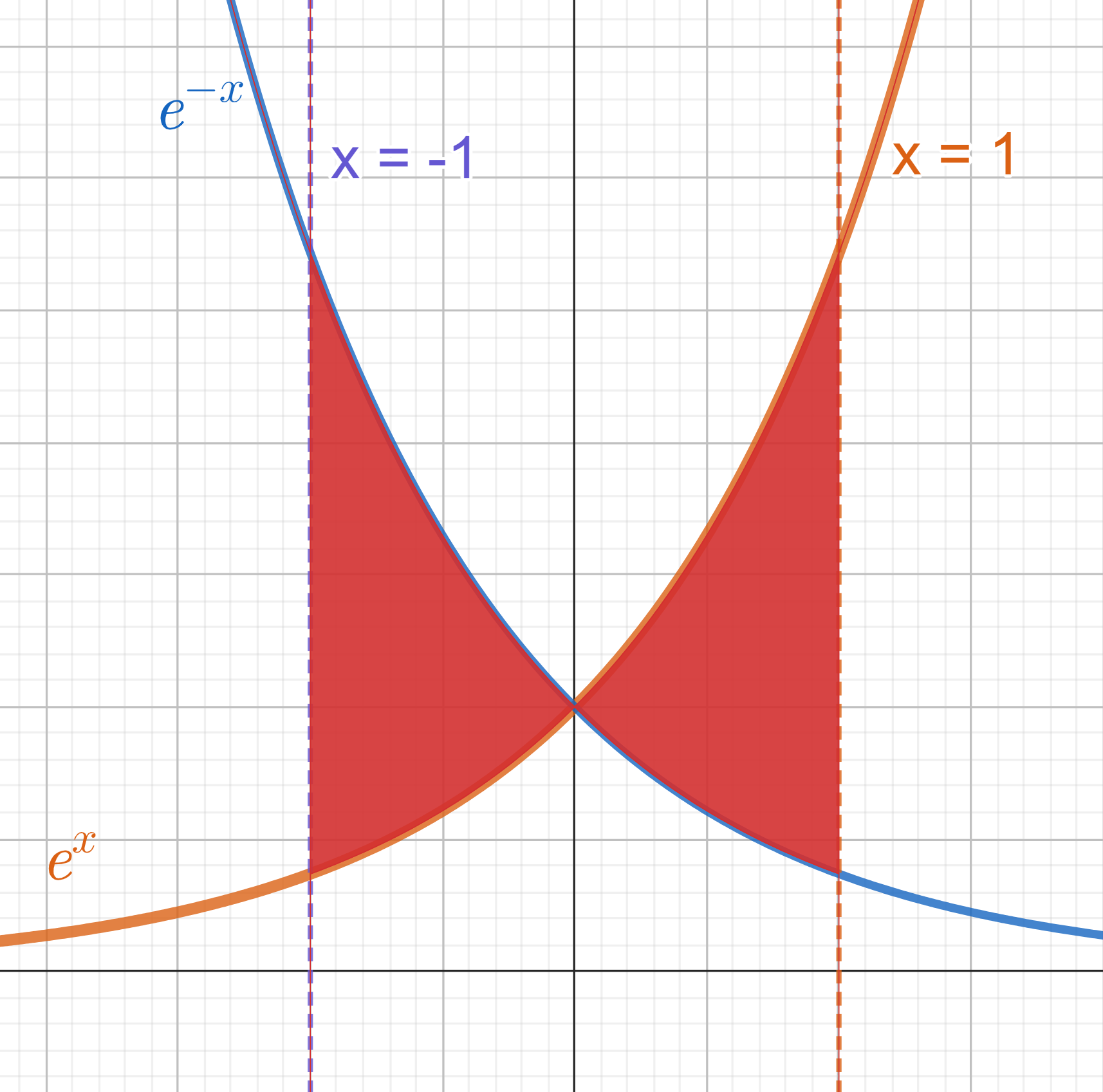
Berechne die Fläche zwischen den Graphen 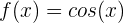 und
und 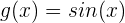 im Intervall
im Intervall 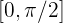 .
.
1
Zunächst analysieren wir die Schnittpunkte dieser Graphen. Beachte, dass für die Punkte  gilt
gilt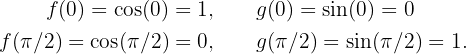
Wir beachten, dass bei 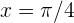 gilt:
gilt: 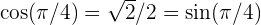 .
.
2
Somit ist die Fläche unter dem Graphen das Integral von  im Intervall
im Intervall 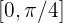 plus das Integral von
plus das Integral von 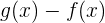 im Intervall
im Intervall 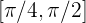 :
: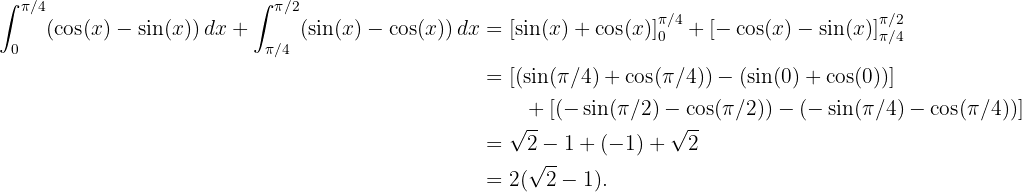
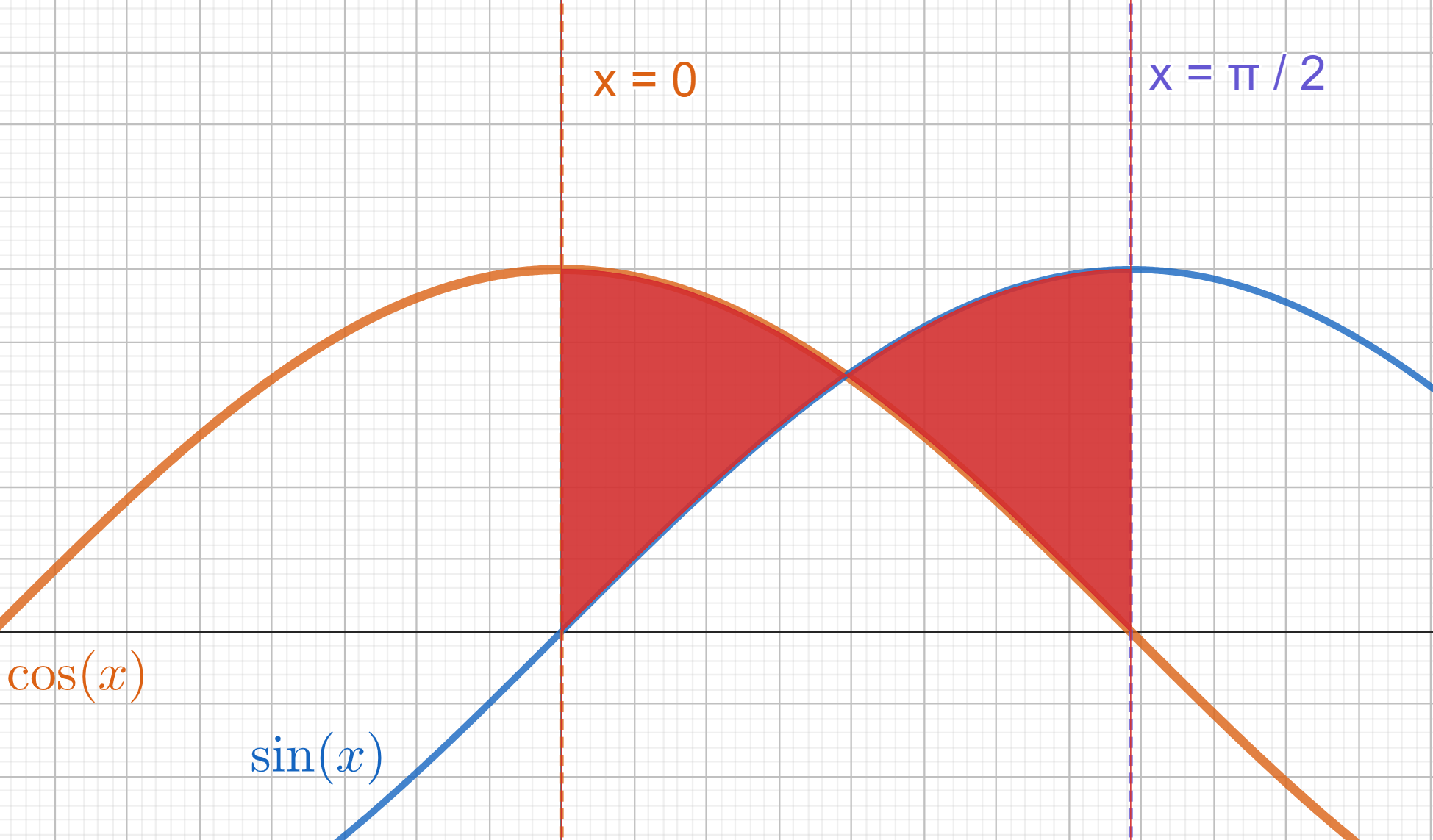
Mit KI zusammenfassen:












