Kapitel
- Der allgemeine Term einer geometrischen Folge
- Interpolation von n Termen einer geometrischen Folge
- Summe von n aufeinanderfolgenden Termen einer geometrischen Folge
- Summe der Terme einer abnehmenden geometrischen Folge
- Produkt aus zwei äquidistanten Termen
- Produkt aus n aufeinanderfolgenden Termen einer geometrischen Folge
Geometrische Folgen haben verschiedene Anwendungen im täglichen Leben, wie z. B. die Berechnung der Zinsen für einen Kredit, wenn man einen Gegenstand kauft oder um das Populationswachstum einer Art zu messen; hier erfährst du etwas über ihre Eigenschaften.
Eine geometrische Folge ist eine Reihe, bei der jeder Term durch Multiplikation des vorhergehenden Terms mit einer festen Größe q, dem sogenannten Quotienten, entsteht.
Beispiel:
Wenn wir einen ersten Term a1=3 und einen Quotienten q=4 haben, können wir folgende geometrische Folge erstellen:
3, 12, 48, 192, ...
Wenn wir also mit dem ersten Term a1=3 und dem Quotienten q=4 rechnen, erhalten wir:
3
3(4)=12
12(4)=48
48(4)=192, ...
Wie du siehst, erhält man 12, indem man 3 mit 4 multipliziert, was der Quotient ist, und so weiter, bis der gewünschte Term n erreicht ist.
Wenn aber zwei aufeinanderfolgende Terme an und an+1 der geometrischen Folge bekannt sind, der Quotient q jedoch nicht, kann der Quotient q durch Division dieser Terme wie in der folgenden Gleichung berechnet werden:
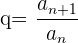
Beispiel:
Gegeben ist die geometrische Folge: 3, 6, 12, 24, 48, ... Wir stellen fest, dass zwei beliebige aufeinanderfolgende Terme den Quotienten q=2 haben. Durch Anwendung der vorhergehenden Gleichung erhält man:
q=6/3=2
q=12/6=2
q=24/12=2
q=48/24=2

Der allgemeine Term einer geometrischen Folge
Der allgemeine Term einer Folge ist der Ausdruck an, der es uns ermöglicht, jeden Term nach seiner n-ten Position zu bestimmen.
Wenn wir den Wert des allgemeinen Terms an bestimmen möchten, können sich zwei Situationen ergeben:
1 Der erste Term a1 und der Quotient q sind bekannt. In diesem Fall ist es möglich, jeden anderen Term der Folge mit Hilfe der folgenden Formel zu ermitteln:
an = a1 · qn-1
Beispiel:
Gegeben ist folgende Folge und du sollst den Wert des Terms, der an 20. Stelle steht, berechnen:
3, 6, 12, 24, 48, ...
Beweise, dass a1=3, der Quotient q=2 und da du den Wert des 20. Terms ermitteln sollst, somit n=20 ist. Wenn du diese Werte in die Formel einsetzt, erhältst du:
a20 = 3· 220-1 = 3· 219 = 1.572.864
Der Wert des 20. Terms ist somit 1.572.864.
2 Der erste Term a1 der geometrischen Folge ist nicht bekannt, allerdings ein anderer Term ak und der Quotient q. In diesem Fall ist es möglich, einen beliebigen Term an mit der folgenden Gleichung zu berechnen:
an = ak · qn-k
Dabei ist k die Nummer der Position des Terms, der bekannt ist, und n die Position des Terms, den man ermitteln möchte.
Beispiel:
Angenommen, ak ist gleich 24, wobei k=4 und der Quotient q=2 ist. Wenn du diese Werte in die Formel einsetzt, erhältst du:
an = a4 · 2n-4
Wenn du nun also den Wert von a1 ermittlen möchtest, rechnest du wie folgt:
a1 = 24· 21-4= (24)· 2-3 = (24)(1/8) =3
Willst du nun den Wert von a10 ermitteln, rechnest du wie im vorhergehenden Beispiel:
a10 = 24· 210-4= (24)· 26 = 1536
Vergiss nicht, dass n die Position des Terms ist, den du ermitteln willst.
Wie du feststellen wirst, spielt es keine Rolle, welchen Term an du ermitteln möchtest, da er je nach Situation mit der entsprechenden Formel berechnet wird.
Interpolation von n Termen einer geometrischen Folge
Geometrische oder proportionale Mittelwerte zwischen zwei Zahlen a und b zu interpolieren, bedeutet, eine geometrische Folge zu konstruieren, die als Extremwerte die Elemente a und b und eine bestimmte Anzahl von Zwischenwerten hat. Um dies zu erreichen, muss man wissen, wie viele Elemente m interpoliert werden sollen, und mit dieser Information den entsprechenden Quotienten q berechnen. Denn mit q und dem Wert von a wird die geometrische Folge erstellt.
Die Formel zur Ermittlung des passenden Quotienten q zur Interpolation von m geometrischen Mittelwerten zwischen a und b lautet:
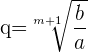
Beispiel:
Interpoliere 3 geometrische Mittelwerte zwischen a=-2 und b=-4802. Als Erstes ermitteln wir den entsprechenden Quotienten q.
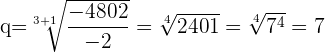
Da bekannt ist, dass q=7 ist, wird dieser Wert verwendet, um die geometrische Folge zu bilden, indem man a=-2 als ersten Wert nimmt und ihn nacheinander mit dem Quotienten q=7 multipliziert, wodurch man erhält:
-2, -14, -98, -686, -4802.
Wir stellen fest, dass wir drei Zahlen zwischen -2 und -4802 interpoliert haben und bilden so die Folge.
Beispiel:
Interpoliere drei geometrische Mittelwerte zwischen a=3 und b=48. Als Erstes ermitteln wir den passenden Quotienten q.
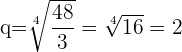
Mit dem ermittelten Quotienten können wir die geometrische Folge bilden und erhalten:
3, 6, 12, 24 , 48.
Auf die gleiche Weise wie im vorherigen Beispiel wurden 3 Zahlen interpoliert, aber nun zwischen 3 und 48, wodurch die gewünschte Folge entsteht.
Zusammenfassend lässt sich sagen, dass man beliebig viele Terme m zwischen a und b interpolieren kann, man muss nur den entsprechenden Quotienten q anhand der Formel berechnen.
Summe von n aufeinanderfolgenden Termen einer geometrischen Folge
Um n aufeinanderfolgende Terme einer geometrischen Folge zu addieren, muss man zunächst den Quotienten q, den ersten Term a1 und die Anzahl der Werte n kennen, die man in der Folge addieren möchte.
Da diese Daten bekannt sind, verwendet man die Formel:
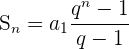
wobei Sn die Summe von n aufeinanderfolgenden Termen einer geometrischen Folge ist.
Beispiel:
Berechne die Summe der ersten 5 Terme der folgenden Folge: 3, 6, 12, 24, 48, ...
Wir berechnen den Quotienten q, indem wir zwei aufeinanderfolgende Terme dividieren
q=6/3 =2
Mit q=2, n=5 und a1 =3 setzen wir nun die Werte in die Formel ein und erhalten:
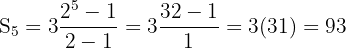
So erhalten wir das Ergebnis der Addition der n gewünschten Terme:
3 + 6 + 12 + 24 + 48 = 93
Ein Vorteil dieses Verfahrens ist, dass die Summe von n Termen sehr viel Arbeit spart, im Gegensatz zur direkten Addition, da die Anzahl der zu addierenden n Terme sehr groß sein kann.
Summe der Terme einer abnehmenden geometrischen Folge
Es gibt Fälle, in denen es notwendig ist, alle Terme einer unbegrenzt abnehmenden geometrischen Folge zu addieren. Damit die Summe einen Sinn ergibt, muss der Wert des Quotienten zwischen -1 und 1 liegen, andernfalls ist es nicht möglich, die Addition vorzunehmen, da sie kein numerisches Ergebnis liefern würde.
Es gibt eine Formel zur Ermittlung des Ergebnisses der Addition aller Terme
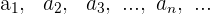
-1 < q < 1 ist:
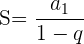
Mit dieser Formel wird die Summe aller Terme der Folge berechnet. Das heißt:

Beispiel:
Berechne die Summe der Terme der unbegrenzt abnehmenden geometrischen Folge, gebildet durch a1=2 und q=0,5.
Wir bedenken, dass der Wert von q zwischen -1 und 1 liegen muss. In unserem Fall ist q=0,5 und somit die Bedingung erfüllt. Wir können also mit unserer Berechnung fortfahren.
Es ergibt sich folgende geometrische Folge:
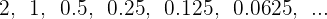
und so weiter (die Auslassungspunkte zeigen an, dass der Prozess noch nicht abgeschlossen ist).
Wir setzen in die Formel ein und erhalten das Ergebnis der Summe aller Terme:
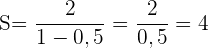
bedeutet:
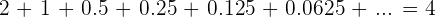
So erhalten wir das gesuchte Ergebnis.
Die Summe, mit der wir jetzt rechnen, unterscheidet sich von der vorhergehenden, da hier eine unbegrenzte Anzahl von Termen addiert wurde (vorher bestand die Summe aus einer begrenzten Anzahl von Termen). Deshalb war es notwendig, die oben genannte Formel zu verwenden.
Produkt aus zwei äquidistanten Termen
Bei einer geometrischen Folge, bei der a1 der erste Term und an der letzte Term ist, sind zwei Werte äquidistant, wenn sie von beiden Enden der Folge gleich weit entfernt sind. Zum Beispiel:
a2 ist äquidistant zu an-1
a3 ist äquidistant zu an-2
a4 ist äquidistant zu an-3
und so weiter.
Ein Rechengesetz besagt, dass die Multiplikation zweier äquidistanter Werte gleich dem Produkt der Extremwerte dieser Folge ist, das heißt:
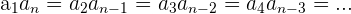
Beispiel:
Wir haben folgende geometrische Folge:
5, 10, 20, 40, 80, 160
Wir sehen, dass das Produkt der Extremwerte
5 (160) = 800
gleich dem Produkt eines beliebigen Paares äquidistanter Terme ist, zum Beispiel:
10 (80) = 800
20 (40) = 800
Dieses Rechengesetz hat den Vorteil, dass nur mit den Extremwerten multipliziert wird, so dass das Ergebnis der Multiplikation eines beliebigen Paares äquidistanter Terme bekannt ist und auch für zukünftige Ergebnisse verwendet werden kann.
Produkt aus n aufeinanderfolgenden Termen einer geometrischen Folge
Will man eine Anzahl n aufeinanderfolgender Terme einer geometrischen Progression multiplizieren, so genügt es, die Werte der Extremwerte a1 und an zu kennen, also das Produkt der Terme
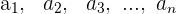
Wir verwenden die Formel:
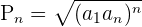
Mit anderen Worten: Die Formel ermöglicht es, das Ergebnis des folgenden Produkts auf effektive Weise zu ermitteln:
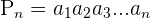
Beispiel:
Berechne das Produkt der ersten 5 Terme der Folge
3, 6, 12, 24, 48, ...
Wir sehen, dass a1 =3 a5 =48 mit n=5:
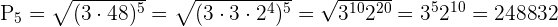
Mit anderen Worten, das Ergebnis lautet wie folgt:
(3) (6) (12) (24) (48) = 248.832
und genau wie bei der Summe von n aufeinanderfolgenden Termen ist es auch hier einfacher und praktischer, das Ergebnis des Produkts mit Hilfe der Formel zu ermitteln, da es eine große Anzahl von Faktoren haben kann.
Mit KI zusammenfassen:












