Kapitel
Konvergente Folgen
Konvergente Folgen sind Folgen, die einen Grenzwert besitzen.
Grenzwert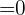 
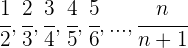
Grenzwert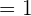 
Divergente Folgen
Divergente Folgen sind Folgen, die keinen Grenzwert besitzen.
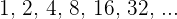
Grenzwerz 
Oszillierende Folgen
Oszillierende Folgen sind weder konvergent noch divergent. Ihre Terme alternieren zwischen dem größten und dem kleinsten Term oder umgekehrt.
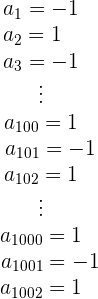
Alternierende Folgen
Alternierende Folgen sind solche, bei denen sich die Vorzeichen der Terme abwechseln. Diese können sein:
Konvergent
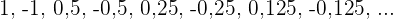
Sowohl die geraden als auch die ungeraden Terme haben den Grenzwert 
.
Divergent
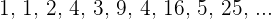
Sowohl die geraden als auch die ungeraden Terme haben den Grenzwert 
.
Oszillierend
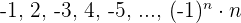
Monotone Folgen
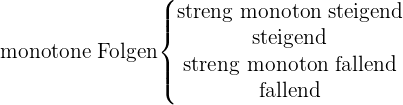
Streng monoton steigende Folgen
Eine Folge ist streng monoton steigend, wenn jeder Term größer als der vorhergehende Term ist.
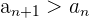
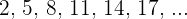
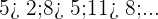
Steigende Folgen
Eine Folge ist steigend, wenn jeder Term größer oder gleich dem vorherigen Term ist.
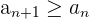
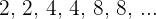
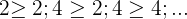
Streng monoton fallende Folgen
Eine Folge ist streng monoton fallend, wenn jeder Term der Folge kleiner ist als der vorherige Term.
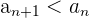
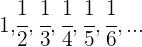
Fallende Folgen
Eine Folge ist fallend, wenn jeder Term der Folge kleiner oder gleich dem vorherigen Term ist.
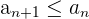
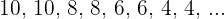
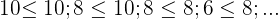
Konstante Folgen
Eine Folge ist konstant, wenn alle ihre Terme gleich sind, also 
.
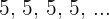
Nach unten beschränkte Folgen
Eine Folge ist nach unten beschränkt, wenn alle ihre Terme größer oder gleich einer bestimmten Zahl K sind, die wir untere Schranke der Folge nennen.
Die größte untere Schranke wird Infimum genannt.
Wenn das Infimum einer Folge einer ihrer Terme ist, nennt man es Mininum.
Nach oben beschränkte Folgen
Eine Folge ist nach oben beschränkt, wenn alle ihre Terme kleiner oder gleich einer bestimmten Zahl K' sind, die wir obere Schranke der Folge nennen.
Die kleinste obere Schranke wird Supremum genannt.
Wenn das Supremum einer Folge einer ihrer Terme ist, nennt man es Maximum.
Beschränkte Folgen
Eine Folge nennt man beschränkt, wenn sie nach oben oder unten beschränkt ist. Das heißt, wenn es eine Zahl k gibt, die kleiner oder gleich allen Termen der Folge ist, und eine andere Zahl K', die größer oder gleich allen Termen der Folge ist. Daher liegen alle Terme der Folge zwischen k und K'.
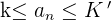
Beispiele für Folgen
1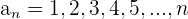 
Steigend
Nach unten beschränkt bei 
Das Minimum ist
Nach oben nicht beschränkt
Divergent
2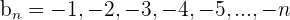 
Fallend
Nach oben beschränkt
Das Maximum ist 
Nach unten nicht beschränkt
Divergent
3 
Fallend
Nach oben beschränkt
Das Maximum ist 
Nach unten beschränkt
Das Infimum ist
Konvergent, Grenzwert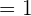
4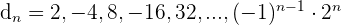 
Nicht monoton
Nicht beschränkt
Weder konvergent noch divergent
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
