Kapitel
In diesem Artikel befassen wir uns mit dem Begriff der Folge und nennen wichtige Definitionen im Zusammenhang damit.
Einleitung
Eine Folge ist eine Menge von Elementen, normalerweise Zahlen, die nacheinander angeordnet sind
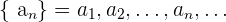
Jedes Element innerhalb der Folge wird als Glied der Folge bezeichnet. Der Index gibt die Stelle an, an der sich das Glied in der Folge befindet. Somit gibt 
das n-te Glied der Folge 
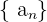an. Zum Beispiel ist 
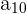das 10. Glied der Folge .
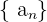Bestimmung einer Folge
Allgemeines Glied
Wir können eine Folge mithilfe dessen bestimmen, was wir als das allgemeine Glied kennen. Das allgemeine Glied hilft uns, den Wert jedes Gliedes der Folge auf der Grundlage seiner Position zu berechnen. Im Allgemeinen haben wir
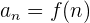
und wir schreiben
Beispiel: Ermittle die ersten 5 Glieder der Folge 
Die Folge ist durch das allgemeine Glied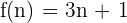 
gegeben
Um die Glieder der Folge zu bestimmen, setzen wir die Werte für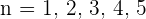 
ein
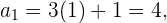
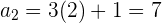
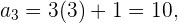
Formal sind Folgen als Funktionen bekannt, die von der Menge der natürlichen Zahlen zur Menge der reellen Zahlen führen, d. h.
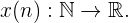
Durch Rekursion
Obwohl die Rekursion nicht sehr formal ist, sieht man häufig Folgen, die nach dieser Methode definiert sind. Die Rekursion besteht darin, eine endliche Anzahl von Gliedern durch einen bestimmten Wert und die anderen durch Operationen zwischen den vorhergehenden Gliedern zu definieren, wobei diese Operationen durch eine Funktion der folgenden Form definiert werden:
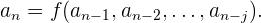
Üblicherweise definieren wir nur das erste Glied mit einem bestimmten Wert und die anderen Glieder als Funktion des unmittelbar vorhergehenden Gliedes.
Beispiel: Ermittle die ersten 5 Glieder der Folge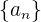 
, die durch 
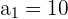und 
für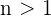 
definiert ist.
Die Glieder der Folge werden durch das vorhergehende Glied definiert, d. h. wenn wir ein Glied kennen, können wir das nächste Glied bestimmen. Wir kennen das 1. Glied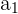 
und können somit das 2. Glied 
bestimmen
Da uns das 2. Glied bekannt ist, können wir das 3. Glied 
bestimmen
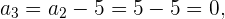
Da wir das 3. Glied kennen, können wir somit das 4. Glied 
bestimmen
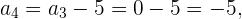
Da wir das 4. Glied kennen, können wir somit das 5. Glied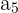 
bestimmen
und erhalten als Ergebnis
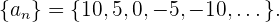
Rechnen mit Folgen
In diesem Teil sehen wir uns Rechenoperationen mit Folgen oder zwischen einer Folge und einer reellen Zahl an.
Addition von Folgen
Wenn wir 2 Folgen 
und 
haben, ist die Summe dieser beiden Folgen eine neue Folge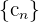 
Kurz gesagt: Wir addieren die Glieder, die sich an der gleichen Stelle befinden.
Beispiel: Berechne die Summe der folgenden Folgen
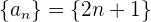
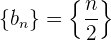
Wir berechnen die Glieder der einzelnen Folgen
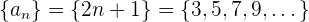
Wir addieren Glied mit Glied und erhalten
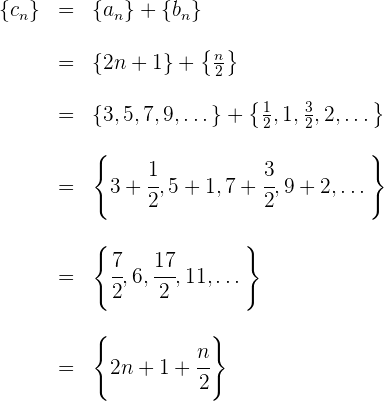
Dabei ist zu beachten, dass das allgemeine Glied der Summe gleich der Summe der allgemeinen Glieder der beteiligten Folgen ist.
Gesetze zur Addition von Folgen
1 Kommutativität: Wenn wir 2 Folgen und haben, gilt
2 Assoziativität: Wenn wir 3 Folgen , und 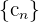haben, gilt
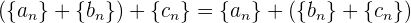
3 Neutrales Element: Es extistiert die Folge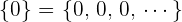 
und somit
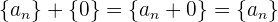
4 Inverses Element: Für jede Folge existiert die Folge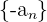 
, die dieselben Elemente wie hat, jedoch mit umgekehrtem Vorzeichen
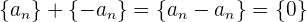
Subraktion von Folgen
Wenn wir 2 Folgen und haben, ist die Differenz 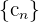dieser Folgen wie folgt definiert
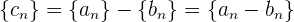
Kurz gesagt: Wir subtrahieren die Glieder, die sich an der gleichen Stelle befinden.
Beispiel: Bestimme die Differenz der folgenden Folgen
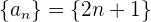
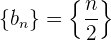
Wir berechnen die Glieder der einzelnen Folgen
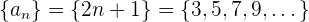
Wir subtrahieren Glied von Glied und erhalten
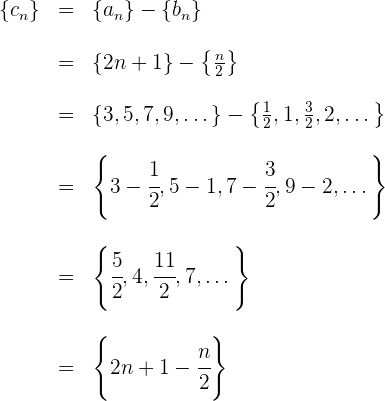
Dabei ist zu beachten, dass das allgemeine Glied der Subtraktion gleich der Subtraktion der allgemeinen Glieder der beteiligten Folgen ist.
Die Differenz aus und ist gleich der Summe aus und 
, wobei der Kehrwert von in Bezug auf die Summe ist.
Multiplikation von Folgen
Wenn wir 2 Folgen und haben, wird die Multiplikation dieser Folgen wie folgt definiert:
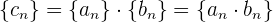
Kurz gesagt: Wir multiplizieren die Glieder, die sich an der gleichen Stelle befinden.
Beispiel: Ermittle das Produkt der folgenden Folgen
Wir berechnen die Glieder der einzelnen Folgen
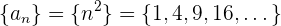
Wir multiplizieren Glied mit Glied und erhalten
Dabei ist zu beachten, dass das allgemeine Glied der Multiplikation gleich der Multiplikation der allgemeinen Glieder der beteiligten Folgen ist.
Eigenschaften der Multiplikation von Folgen
1 Kommutativität: Wenn wir 2 Folgen und haben, gilt
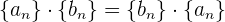
2 Assoziativität: Wenn wir 3 Folgen , und 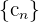haben, gilt
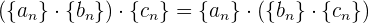
3 Neutrales Element: Es existiert eine Folge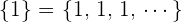 
und somit
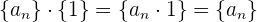
4 Inverses Element: Für jede Folge , sodass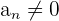 
für alle 
, existiert die Folge 
, die die Kehrwerte der Elemente von enthält und folgende Bedingung erfüllt:
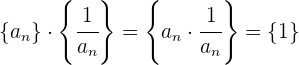
5 Distributivität in Bezug auf die Summe: Wenn wir 3 Folgen , und 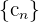haben, gilt
Division von Folgen
Wenn wir 2 Folgen und haben, ist die Division dieser Folgen wie folgt definiert:
Kurz gesagt: Wir dividieren die Glieder, die sich an gleicher Stelle befinden. Dabei ist zu beachten, dass die Glieder von nicht null sein dürfen, da die Division durch null nicht genau definiert ist.
Beispiel: Bestimme die Division von 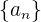durch 
Wir berechnen die Glieder der einzelnen Folgen
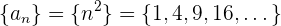
Wir dividieren Glied durch Glied und erhalten
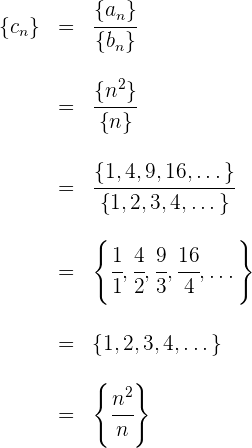
Dabei ist zu beachten, dass das allgemeine Glied der Division gleich der Division der allgemeinen Glieder der beteiligten Folgen ist.
Die Division von und entspricht der Multiplikation von und 
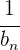, wobei 
der Kehrwert von in Bezug auf die Multiplikation ist.
Grenzwert einer Folge
Gegeben ist eine Folge . Wir sagen, dass der Grenzwert derjenige Wert ist, dem sich die Elemente der Folge nähern, wenn zunimmt. Im Allgemeinen wird der Grenzwert mit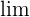 
ausgedrückt.
Beispiel: Bestimme den Grenzwert der Folge
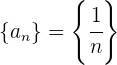
Die Glieder der Folge sind:
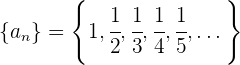
Dabei ist zu beachten, dass mit wachsendem das Glied kleiner wird.
Die Folge hat den Grenzwert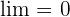 
. Das liegt daran, dass sich bei wachsendem 
gegen 0 bewegt.
Allerdings haben nicht alle Folgen einen Grenzwert, in diesem Fall gibt es drei Möglichkeiten:
1 Konvergent. Eine Folge ist konvergent, wenn sie einen Grenzwert hat.
2 Nicht konvergent. Eine Folge ist nicht konvergent, wenn sie keinen Grenzwert hat.
3 Divergent. Eine Folge divergiert nach unendlich oder minus unendlich, wenn sich ihre Glieder mit wachsendem unendlich (
) bzw. minus unendlich (
) nähern.
Beispiele: Die Folge
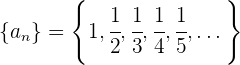
ist konvergent, da .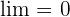
Die Folge
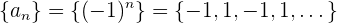
hat keinen Grenzwert, da ihre Elemente zwischen 
und 
alternieren, weshalb sie nicht konvergent ist.
Die Folge
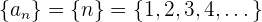
ist divergent, da ihre Glieder mit zunehmendem immer weiter zunehmen.
Monotone Zahlenfolgen
In diesem Teil sehen wir uns Folgen im Hinblick darauf an, wie wir jedes aufeinanderfolgende Gliederpaar vergleichen.
Monoton steigende Folge
Eine Folge ist monoton steigend (oder monoton wachsend), wenn für jedes Paar von aufeinanderfolgenden Gliedern und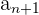 
gilt, dass
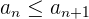
Beispiel: Für die Folge
beachten wir, dass
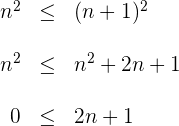
Die letzte Ungleichung gilt für das gesamte , weshalb die Folge monoton steigend ist.
Streng monoton steigende Folge
Eine Folge ist streng monoton steigend, wenn für jedes Paar von aufeinanderfolgenden Gliedern und 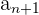Folgendes gilt:
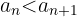
Beispiel: Für die Folge
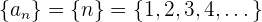
beachten wir, dass:
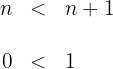
Die letzte Ungleichung ist immer erfüllt, weshalb die Folge streng monoton steigt.
Monton fallende Folge
Eine Folge ist monoton fallend, wenn für jedes Paar an aufeinanderfolgenden Gliedern und 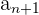Folgendes gilt:
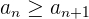
Beispiel: Für die Folge
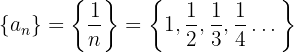
beachten wir, dass:
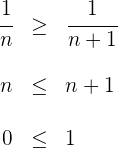
Die letzte Ungleichung gilt für alle , weshalb die Folge monoton fallend ist.
Streng monton fallende Folge
Eine Folge ist streng monoton fallend, wenn für jedes Paar an aufeinanderfolgenden Gliedern und 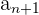Folgendes gilt:
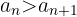
Beispiel: Für die Folge
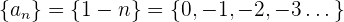
beachten wir, dass
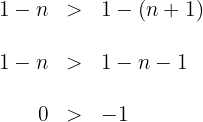
Die letzte Ungleichung ist immer erfüllt, weshalb die Folge streng monoton fallend ist.
Beschränktheit von Folgen
Hier werden wir sehen, was eine beschränkte Folge ist und welche verschiedenen Arten von Schranken es gibt.
Nach unten beschränkte Folge
Eine Folge ist nach unten beschränkt, wenn eine reelle Zahl 
exisitert, sodass
Kurz gesagt: Wenn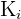 
kleiner oder gleich aller Glieder der Folge ist. In diesem Fall sagen wir, dass 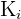eine untere Schranke von ist. Dabei ist zu beachten, dass jede reelle Zahl 
, die
erfüllt,
eine untere Schranke von ist.
Beispiel: Für die Folge
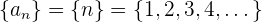
gilt immer, dass
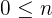
Somit ist 
eine untere Schranke von . Deshalb ist eine nach unten beschränkte Folge. Ebenso sind die Zahlen und 
untere Schranken von .
Nach oben beschränkte Folge
Eine Folge ist nach oben beschränkt, wenn eine reelle Zahl 
existiert, sodass
Kurz gesagt: Wenn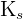 
größer oder gleich aller Glieder der Folge ist. In diesem Fall sagen wir, dass 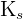eine obere Schranke von ist. Dabei ist zu beachten, dass jede reelle Zahl , die
erfüllt,
eine obere Schranke von ist.
Beispiel: Für die Folge
gilt immer, dass
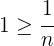
Somit ist eine obere Schranke von . ist also eine nach oben beschränkte Folge. Ebenso sind die Zahlen 
und 
obere Schranken von .
Beschränkte Folge
Eine Folge ist beschränkt, wenn sie nach unten und oben beschränkt ist. Kurz gesagt: Wenn es reelle Zahlen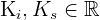 
gibt, sodass
Eine andere äquivalente Definition lautet, dass beschränkt ist, wenn es eine reelle Zahl 
gibt, für die gilt
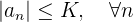
Beispiel: Für die Folge, die wir zuvor untersucht haben
gilt immer, dass
.
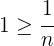Somit ist eine obere Schranke von .
Außerdem ist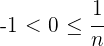 
für alle , weshalb
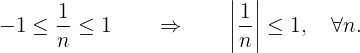
Somit ist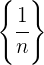 
eine beschränkte Folge.
Arithmetische Folgen
Eine arithmetische Folge ist eine Folge von Zahlen, bei der jedes Glied gleich einer festen Zahl 
plus 
mal einem Betrag 
(Differenz) ist. Die Formel ist gegeben durch
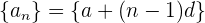
oder auch
Dabei ist zu beachten, dass die Folge für und vollständig definiert ist. Außerdem ist die Formel der einer Geraden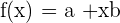 
sehr ähnlich, wobei unsere Werte für 
nur natürliche Zahlen sein können.
Beachte, dass für eine arithmetische Folge immer gilt, dass
Aus diesem Grund wird oft gesagt, dass eine arithmetische Folge die folgende Form hat
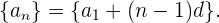
Beispiel: Ermittle die Glieder der arithmetischen Folge
Hierbei ist 
und 
Wir werten das allgemeine Glied für die verschiedenen Werte von aus
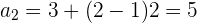
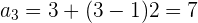
Wir sehen, dass sich zwei aufeinanderfolgende Glieder um unterscheiden
Geometrische Folgen
Eine geometrische Folge ist eine Folge von Zahlen, bei der jedes Glied einer festen Zahl multipliziert mit einer Menge 
zur Potenz 
entspricht. Die Formel ist gegeben durch
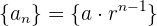
Diese Folge ist für und vollständig definiert.
Beachte, dass für eine geometrische Folge immer gilt, dass
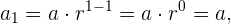
Aus diesem Grund wird oft gesagt, dass eine geometrische Folge die folgende Form hat
Beispiel: Bestimme die Glieder der geometrischen Folge
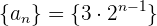
Hierbei ist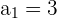 
und 
Wir werten das allgemeine Glied für die verschiedenen Werte von aus
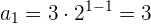
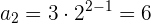
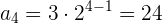
Allgemeines Glied einer Folge
Hier sind einige Empfehlungen, um das allgemeine Glied zu bestimmen
1 Überprüfe, ob es sich um eine arithmetische Folge handelt.
2 Überprüfe, ob es sich um eine geometrische Folge handelt.
3 Überprüfe, ob die Glieder Quadratzahlen sind.
4 Wenn die Glieder der Folge abwechselnd das Vorzeichen wechseln. In diesen Fällen gibt es normalerweise ein Glied 
(positive gerade Zahlen) oder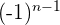 
(positive ungerade Zahlen), mit dem die Glieder multipliziert werden, sodass sie alternieren.
5 Sind die Glieder der Folge Brüche (es handelt sich nicht um eine Folge), so wird das allgemeine Glied von Zähler und Nenner getrennt berechnet.
Beispiel: Ermittle das allgemeine Glied der Folge
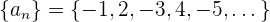
Wir stellen fest, dass die Glieder im Betrag fortlaufend sind.
Das Vorzeichen des ersten Glieds ist negativ, danach alternieren die Vorzeichen. Somit ist das allgemeine Glied gegeben durch
Beispiel: Ermittle das allgemeine Glied der Folge
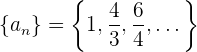
Wir stellen fest, dass der Zähler des 2. und 3. Glieds aufeinanderfolgende gerade Zahlen sind und schlagen somit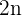 
vor.
Ebenso sind der Nenner des 2. und 3. Glieds aufeinanderfolgende ganze Zahlen, so dass wir 
vorschlagen.
Das vorgeschlagene allgemeine Glied ist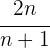 
.
Wir überprüfen, ob das vorgeschlagene allgemeine Glied das 1. Glied erfüllt
.
Da die angegebenen Glieder den vorgeschlagenen Ausdruck erfüllen, kommen wir zu dem Schluss, dass
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
