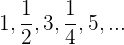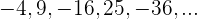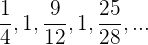Kapitel
Allgemeines Glied und Eigenschaften
Bestimme das allgemeine Glied der Folgen:
a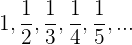 
Zähler
Er ist konstant gleich 
Nenner
Es handelt sich um eine arithmetische Folge von 
Sie beginnt bei 1, da der Nenner durch 
gegeben ist
b 
Zähler
Es handelt sich um eine arithmetische Folge mit
Sie beginnt bei , da der Nenner durch gegeben ist
Nenner
Es handelt sich um eine arithmetische Folge von
Sie beginnt bei 
, da der Zähler durch 
gegeben ist
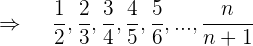
c 
Bei dieser Folge wurden einige Brüche vereinfacht.
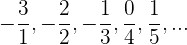
Zähler
Es handelt sich um eine arithmetische Folge mit
Sie beginnt bei 
, da der Zähler durch 
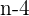gegeben ist
Nenner
Es handelt sich um eine arithmetische Folge von
Sie beginnt bei , da der Zähler durch gegeben ist
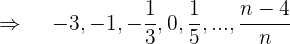
d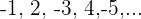 
Wenn wir das Vorzeichen weglassen, handelt es sich um eine arithmetische Folge mit
Da die ungeraden Glieder negativ sind, multiplizieren wir mit 
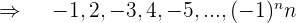
e 
Bei dieser Folge wurden einige Brüche vereinfacht.
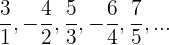
Zähler
Wenn wir das Vorzeichen weglassen, handelt es sich um eine arithmetische Folge mit
Sie beginnt bei 
, da der Zähler durch 
gegeben ist
Nenner
Es handelt sich um eine arithmetische Folge von
Sie beginnt bei 1, da der Zähler durch gegeben ist
Da die geraden Glieder negativ sind, multiplizieren wir mit (–1) n+1
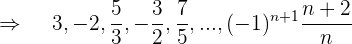
f 
Es handelt sich um eine oszillierende Folge
Die ungeraden Glieder bilden eine arithmetische Folge mit , wenn wir die geraden Glieder nicht beachten
Der Nenner der geraden Glieder bildet eine arithmetische Folge mit 
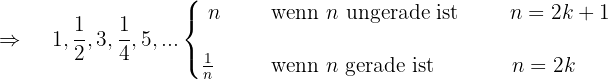
g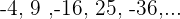 
Wir können die Folge wie folgt schreiben
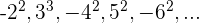
Wenn wir das Vorzeichen und den Exponenten weglassen, haben wir eine arithmetische Folge mit una
Da die Glieder quadriert sind, müssen wir das allgemeine Glied quadrieren
Da die ungeraden Glieder negativ sind, multiplizieren wir mit
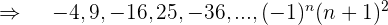
h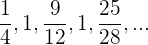 
Wir können die Folge wie folgt schreiben
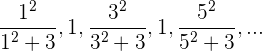
Es handelt sich um eine oszillierende Folge
Zähler
Der Zähler der ungeraden Glieder bildet eine arithmetische Folge mit , wenn man die geraden Glieder außer Acht lässt.
Da die Glieder quadriert sind, müssen wir das allgemeine Glied quadrieren
Nenner
Der erste Summand des Nenners (ohne das Quadrat) ist eine arithmetische Folge von (gerade Glieder nicht mitgezählt)
Wir müssen das allgemeine Glied quadrieren und dazu addieren
Die geraden Glieder bilden eine konstante Folge.
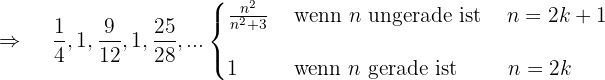
Untersuche die Monotonie, die Konvergenz oder Divergenz sowie die Schranken (sofern vorhanden) der folgenden Folgen:
a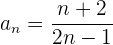 
Wir berechnen die ersten Glieder
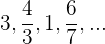
Sie ist streng monoton fallend.
Wenn wir außerdem die sehr großen Werte von berechnen, erhalten wir
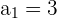
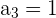
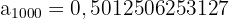
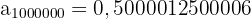
Es handelt sich also um eine konvergente Folge und der Grenzwert ist 0,5.
Da sie fällt, ist 3 eine obere Schranke, das Maximum
0,5 ist eine untere Schranke, das Infimum
Die Folge ist also beschränkt
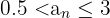
b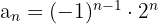 
Wir berechnen die ersten Glieder
Sie ist nicht monoton
Sie ist weder konvergent noch divergent
Sie ist nicht beschränkt
c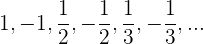 
Sie ist nicht monoton
Sie ist konvergent, da der Grenzwert = 0 ist
Sie ist nach oben beschränkt, 1 ist das Maximum
Sie ist nach unten beschränkt, –1 ist das Minimum
Sie ist beschränkt
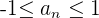
Finde die Folge
Das vierte Glied einer arithmetischen Folge ist 10 und das sechste Glied ist 16. Schreibe die Folge.
Die bekannten Glieder sind
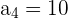
Wir wenden die Formel an
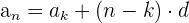
Wir können 
berechnen
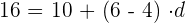
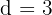
Mit der gleichen Formel können wir das erste Glied der Folge berechnen
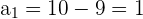
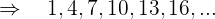
Das zweite Glied einer geometrischen Folge ist 6, das fünfte Glied ist 48. Schreibe die Folge
Die bekannten Glieder sind
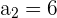
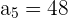
Wir wenden die Formel an
Wir können 
berechnen
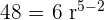
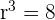
Mit der gleichen Formel berechnen wir das erste Glied
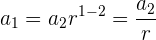
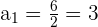
Berechne die Summe, die Differenz oder das Produkt von Gliedern
Finde die Summe der ersten 15 Vielfachen von 5
Wir möchten die Summe der ersten 15 Glieder der Folge erhalten
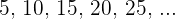
Folgende Werte sind bekannt
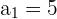
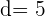
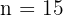
Wir ermitteln das 15. Glied mit der folgenden Formel
Wir wenden die Formel an
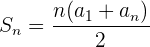
Wir können die Summe der ersten 
Glieder berechnen
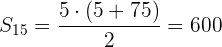
Finde die Summe der ersten 15 Zahlen, die auf 
enden
Wir möchten die Summe der ersten 15 Glieder der Folge erhalten
Folgende Werte sind bekannt
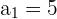
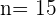
Wir ermitteln das 15. Glied mit der folgenden Formel
Mit der Formel
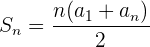
Wir können die Summe der ersten Glieder berechnen
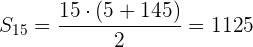
Finde die Summe der ersten 15 geraden Zahlen größer als
Wir möchten die Summe der ersten 15 Glieder der Folge erhalten
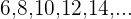
Folgende Werte sind bekannt
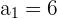
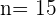
Wir ermitteln das 15. Glied mit der folgenden Formel
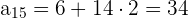
Mit der Formel
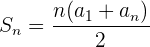
Wir können die Summe der ersten Glieder berechnen
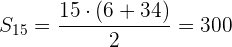
Der erste Glied einer arithmetischen Folge ist 
und das 15. Glied ist 
. Bestimme die Differenz und die Summe der ersten 15 Glieder.
Folgende Werte sind bekannt
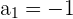
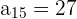
Wir wenden die Formel an
Wir können den Wert von berechnen
Mit der Formel
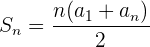
Wir können die Summe der ersten Glieder berechnen
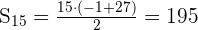
Das erste Glied einer geometrischen Folge ist und das achte Glied ist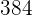 
. Berechne den Quotienten, die Summe und das Produkt der ersten Glieder 
Folgende Werte sind bekannt
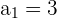
Wir wenden die Formel an
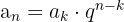
Wir können den Wert von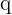 
berechnen
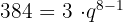
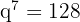
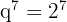
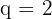
Mit der Formel
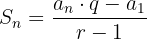
Wir können die Summe der ersten acht Glieder berechnen
Wir betrachten nun die Formel für das Produkt
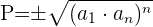
Um das Produkt der ersten Terme zu erhalten
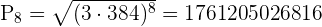
Arithmetische und geometrische Mittel
Schreibe drei arithmetische Mittel zwischen und 
Wir haben folgende Werte
Wir wenden die Formel an
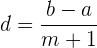
Wir können den Wert von berechnen
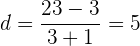
Schließlich
Interpoliere drei geometrische Mittel zwischen und 
Wir haben folgende Werte
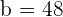
Wir wenden die Formel an
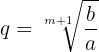
Wir können den Wert von 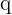berechnen
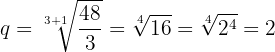
Schließlich
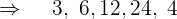
Ermittle den entsprechenden Bruch
Schreibe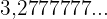 
als Bruch
Wir schreiben die Zahl wie folgt
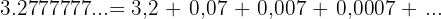
Wir haben eine unbegrenzt abnehmende geometrische Folge
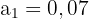
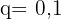
Somit
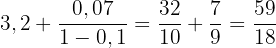
Geometrische Folgen
Berechne die Winkel eines konvexen Vierecks, wenn du weißt, dass sie eine arithmetischer Folge bilden, wobei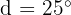 
Die Summe der Innenwinkel eines Vierecks ist:
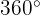
Die vier Winkel bilden eine arithmetische Folge:
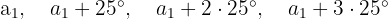
Die Winkelsumme ergibt:
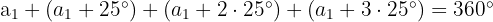
Zusammengefasst:
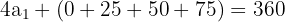
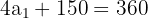
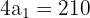
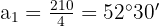
Die weiteren Winkel sind:
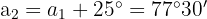
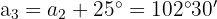
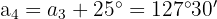
Der kleinste Schenkel eines rechtwinkligen Dreiecks misst 8 cm. Berechne die beiden anderen, wobei du weißt, dass die Seiten des Dreiecks eine arithmetische Folge bilden
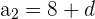
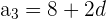
Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck die Hypotenuse zum Quadrat gleich der Summe der Schenkel zum Quadrat ist.
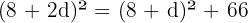
Die negative Lösung ist nicht gültig, da es keine negativen Seiten gibt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
