Kapitel
Willkommen in unserer Rubrik "Aufgaben zu geometrischen Folgen". Geometrische Folgen sind ein faszinierender Bereich der Mathematik, der in zahlreichen Kontexten zu finden ist, vom
exponentiellen Wachstum bis hin zu Berechnungen im Finanzwesen. In diesem Abschnitt geben wir dir detaillierte Lösungen zu einer Reihe von Aufgaben, die geometrische Folgen beinhalten, mit dem Ziel, dein Verständnis und deine Fähigkeiten in diesem Bereich zu stärken.
Jede gelöste Aufgabe wird klar und systematisch dargestellt und führt dich Schritt für Schritt durch den Lösungsprozess. Wir werden Konzepte wie das allgemeine Glied, die Summe der Glieder und andere Schlüsseleigenschaften von geometrischen Folgen untersuchen. Diese Übungen werden dir nicht nur ein besseres Verständnis der Theorie vermitteln, sondern dir auch praktische Werkzeuge an die Hand geben, um reale Probleme mit diesen Arten von Folgen zu lösen.
Wir möchten dich dazu ermutigen, dir diese Aufgaben mit Lösungen anzusehen und die Gelegenheit zu nutzen, dein Wissen zu festigen und geometrische Folgen effektiv in einer Vielzahl von mathematischen und praktischen Szenarien anzuwenden.
Aufgaben
Das 2. Glied einer geometrischen Folge ist 
und das 5. Glied ist 
. Schreibe die Folge.
Das 2. Glied einer geometrischen Folge ist und das 5. Glied ist .
Schreibe die Folge.
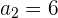
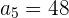
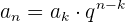
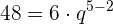
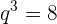
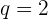
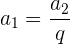
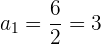
Das 1. Glied einer geometrischen Folge ist 
und das 8. Glied ist 
. Bestimme den Quotienten sowie die Summe und das Produkt der ersten 8 Glieder.
Das 1. Glied einer geometrischen Folge ist und das 8. Glied ist .
Bestimme den Quotienten sowie die Summe und das Produkt der ersten 8 Glieder.
;
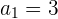
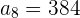Berechnung des Quotienten
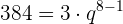
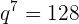
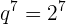
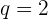
Summe von n Termen:
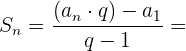
Produkt aus n Termen:
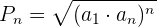
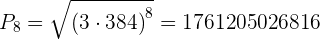
Interpoliere drei geometrische Mittel zwischen und .
Interpoliere drei geometrische Mittel zwischen und .
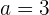
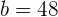
Berechnung des Quotienten:
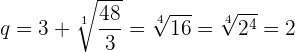
Schreibe die Glieder:
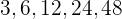
Berechne die Summe der ersten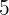 
Glieder der Folge:
Berechne die Summe der ersten 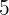Glieder der Folge:
Berechne die Summe der Glieder der streng monoton fallenden geometrischen Folge: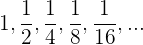 
Berechne die Summe der Glieder der streng monoton fallenden geometrischen Folge:
Wir berechnen den Quotienten: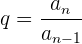
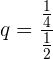
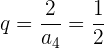
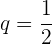
Wir wenden die Formel für die Summe von n Gliedern an.
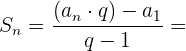
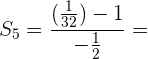
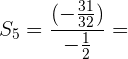
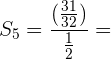
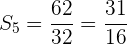
Berechne das Produkt der ersten 5 Glieder der Folge:
Berechne das Produkt der ersten 5 Glieder der Folge:
Wir wenden die Formel für das Produkt aus n Gliedern an:
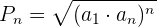
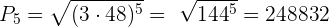
Jan hat 20 Bücher gekauft. Für das 1. Buch hat er 1 Euro bezahlt, für das 2. Buch 2 Euro, für das 3. Buch 4 Euro, für das 4. Buch 8 Euro und so weiter. Wie viel hat er insgesamt für die Bücher bezahlt?
Jan hat 20 Bücher gekauft. Für das 1. Buch hat er 1 Euro bezahlt, für das 2. Buch 2 Euro, für das 3. Buch 4 Euro, für das 4. Buch 8 Euro und so weiter. Wie viel hat er insgesamt für die Bücher bezahlt?
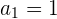
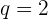
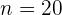
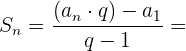
Wir berechnen das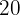 
. Glied:
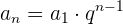
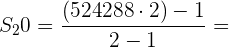
Verbindet man die Mittelpunkte der Seiten eines Quadrats mit der Seitenlänge 
, so erhält man ein weiteres Quadrat. Wenn man diesen Vorgang wiederholt, erhält man wieder ein Quadrat usw. Berechne die Summe der Flächen der unendlichen Quadrate.
Verbindet man die Mittelpunkte der Seiten eines Quadrats mit der Seitenlänge , so erhält man ein weiteres Quadrat. Wenn man diesen Vorgang wiederholt, erhält man wieder ein Quadrat usw.
Berechne die Summe der Flächen der unendlichen Quadrate.
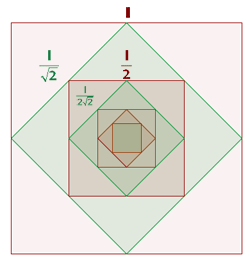
Mit dem Satz des Pythagoras können wir das 2. Glied der Folge berechnen:
Da wir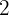 
Glieder haben, können wir den Quotienten berechnen:
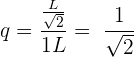
Die Folge lautet:
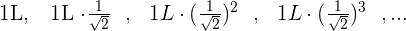
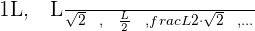
Wir quadrieren jedes Glied, um uns die Folge besser vorstellen zu können:
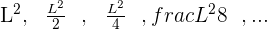
Wir wenden die Formel zur Berechnung der Summe von n Gliedern an. Hierzu nutzen wir den Grenzwert. Beachte: Wenn n im Nenner gegen unendlich geht, geht der Wert des Bruchs gegen null.
Ermittle den entsprechenden Bruch der Zahl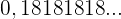 
Ermittle den entsprechenden Bruch der Zahl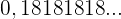
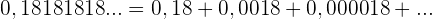
Hierbei handelt es sich um eine streng monoton fallende geometrische Folge.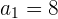
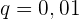
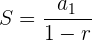
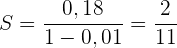
Ermittle den entsprechenden Bruch der Zahl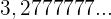 
Ermittle den entsprechenden Bruch der Zahl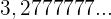
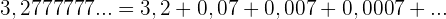
Wir haben eine streng monoton fallende Folge
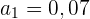
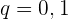
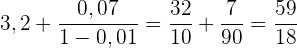
Ermittle den entsprechenden Bruch der Zahl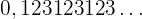 
Die Zahl kann wie folgt dargestellt werden
Wir gehen von einer Anfangsinvestition von 5.000 € und einem festen Zinssatz von 8 % pro Monat aus. Wie viel wird die Investition nach 10 Monaten wert sein, wenn die Erträge in einer geometrischen Folge reinvestiert werden?
Bei einer Anfangsinvestition von 5.000 € mit einem festen Zinssatz von 8 % pro Monat wird der Wert der Investition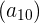 
nach 10 Monaten mihilfe der Formel der geometrischen Folge berechnet:
,
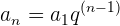wobei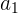 
die Anfangsinvestition, 
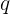der Quotient des Wachstums (1 + Zinssatz) und 
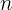die Anzahl der Monate ist. Somit
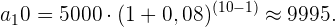
Ein Darlehen von 10.000 €, das in 12 Monaten mit einem Zinssatz von 5 % pro Monat zurückgezahlt werden soll, wird monatlich in geometrischer Folge getilgt. Wie viel muss am Ende von 12 Monaten allein an Zinsen gezahlt werden?
Die monatliche Rückzahlungsrate für ein Darlehen von 10.000 €, das in 12 Monaten mit einem Zinssatz von 5 % pro Monat zurückgezahlt werden soll, lässt sich mit der Formel der geometrischen Folge berechnen: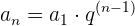
,
wobei 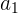der Darlehensbetrag, 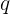der Quotient des Wachstums (1 + Zinssatz) und 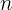die Anzahl der Monate ist. Somit muss insgesamt folgender Betrag bezahlt werden
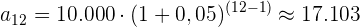
Das heißt, dass 17.103€ - 10.000€ = 7.103€ Zinsen bezahlt werden müssen.
Der Wert eines Vermögens sinkt um 15 % pro Monat. Wenn der ursprüngliche Wert 50.000 Euro beträgt, wie viel ist das Vermögen bei einer geometrischen Folge der Wertminderung nach 6 Monaten noch wert?
Wenn der Wert eines Vermögens um 15 % pro Monat sinkt, wird der Wert des Vermögens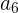 
nach 6 Monaten mithilfe der Formel für die geometrische Folge berechnet: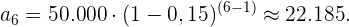
Angenommen, eine Anfangsinvestition von 10.000 € wird zu einem festen Zinssatz von 5 % pro Jahr getätigt. Wie viele Jahre muss man warten, um die Investition zu verdoppeln?
Wir wollen herausfinden, wie viele Jahre es dauert, bis die Investition 20.000 € erreicht. Wir beachten, dass die geometrische Folge durch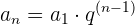 
gegeben ist. Wir ermitteln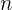 
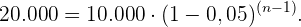
Wir lösen nach 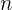auf:
,
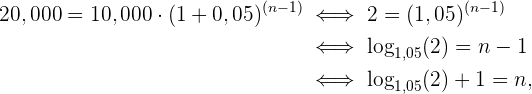wobei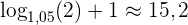 
. Das heißt, dass es 16 Jahre dauert, bis sich die Investition verdoppelt hat.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
