Kapitel
- Grenzwerte, wenn die Variable gegen unendlich konvergiert
- Grenzwert des Quotienten von Polynomen mit Zähler und Nenner gleichen Grades
- Grenzwert des Quotienten von Polynomen, bei denen der Zähler einen höheren Grad hat als der Nenner
- Grenzwert des Quotienten, wenn der Nenner einen höheren Grad als der Zähler hat

Grenzwerte, wenn die Variable gegen unendlich konvergiert
Bei der Berechnung des Grenzwerts des Quotienten von Polynomen durch direkte Substitution kommt es häufig vor, dass die Operation unbestimmt ist. Im folgenden Fall ist der Quotient beispielsweise unbestimmt, wenn eine direkte Substitution vorgenommen wird:
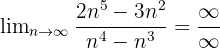
In diesem Fall ist es noch nicht möglich zu sagen, ob der Grenzwert existiert oder nicht.
Andererseits zeigt eine grafische Analyse dieser Funktion, dass mit zunehmendem Wert von n auch der Wert von 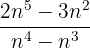 zunimmt; daraus lässt sich ableiten, dass der Grenzwert dieses Quotienten, wenn n gegen unendlich konvergiert, unendlich ist.
zunimmt; daraus lässt sich ableiten, dass der Grenzwert dieses Quotienten, wenn n gegen unendlich konvergiert, unendlich ist.
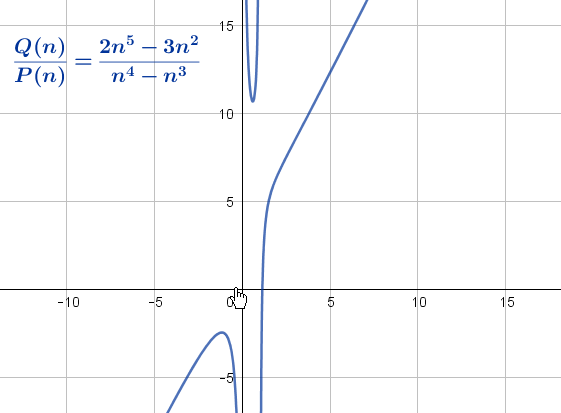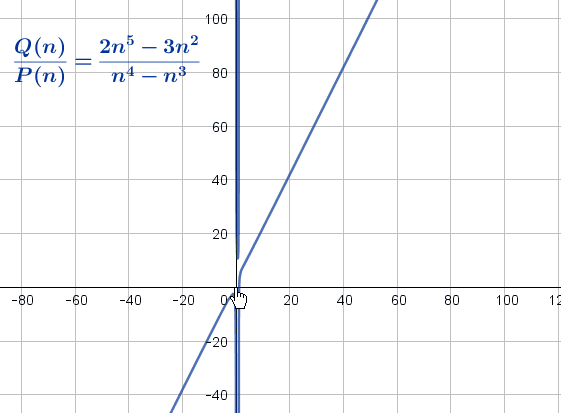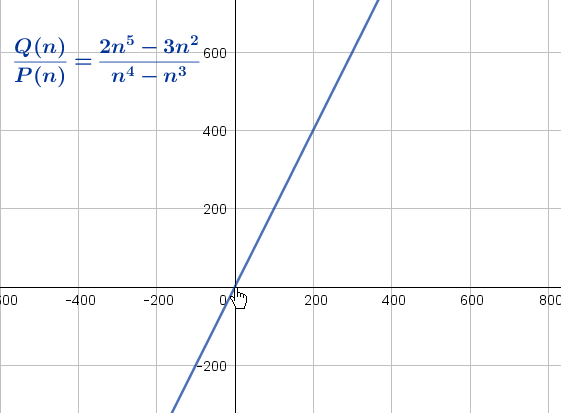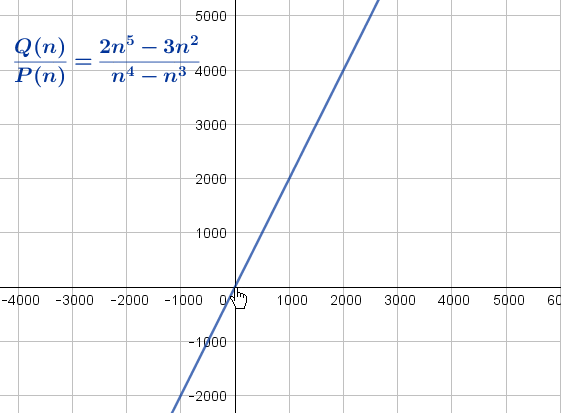
Um ihn algebraisch zu berechnen, muss der Quotient manchmal mit einem „ günstigen Wert“ so bearbeitet werden, dass der Ausdruck zur Bestimmung des Grenzwertes vereinfacht wird. Um zum Ausgangsbeispiel zurückzukehren, können wir den Quotienten mit 1 multiplizieren und ihn wie folgt umschreiben:
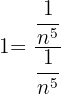
Multipliziert man also den Zähler und den Nenner des Quotienten mit 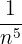 , so erhält man den folgenden Ausdruck:
, so erhält man den folgenden Ausdruck:
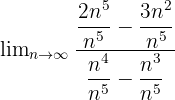
Daraus lässt sich vereinfacht schließen, dass der Grenzwert unendlich ist:
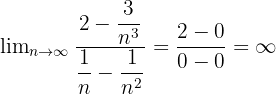
Wie man sieht, ist es nicht immer möglich oder effizient, eine grafische Analyse durchzuführen oder zu bestimmen, wie der algebraische Ausdruck bearbeitet werden kann, um festzustellen, ob der Grenzwert existiert und wie er lautet. Aus diesem Grund ist es nützlich, einige Regeln zu kennen, die uns eine direkte Berechnung ermöglichen.
Grenzwert des Quotienten von Polynomen mit Zähler und Nenner gleichen Grades
Wenn Zähler und Nenner denselben Grad haben, ist der Grenzwert bei n gegen unendlich der Quotient der Koeffizienten der Potenzen höheren Grades.
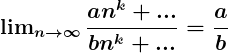
Beispiele
1 Berechne den Grenzwert von 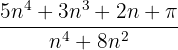 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
Wie man sieht, ist der Grad des Polynoms von Zähler und Nenner 4, daher ist der Grenzwert der Quotient der Koeffizienten der Monome höheren Grades, d.h.:
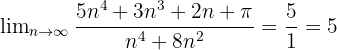
2 Berechne den Grenzwert von 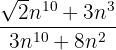 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
In diesem Fall ist der Grad des Polynoms von Zähler und Nenner 10, so dass der Grenzwert der Quotient der Monome höheren Grades ist, das heißt:
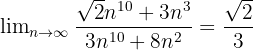
Grenzwert des Quotienten von Polynomen, bei denen der Zähler einen höheren Grad hat als der Nenner
Wenn der Zähler einen höheren Grad als der Nenner hat, ist der Grenzwert, wenn n gegen unendlich konvergiert, ± ∞, abhängig vom Vorzeichen des Koeffizienten höheren Grades.
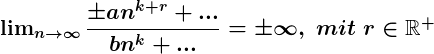
Beispiel
1 Berechne den Grenzwert von 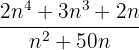 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
Wie man sieht, ist der Grad des Polynoms des Zählers 4 und der des Nenners 2, so dass der Grenzwert unendlich sein muss, und da der Koeffizient positiv ist, ist der Grenzwert unendlich positiv, d.h.:
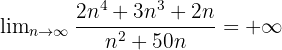
2 Berechne den Grenzwert von 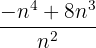 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
In diesem Beispiel ist der Grad des Polynoms im Zähler 4 und der des Nenners 2, so dass der Grenzwert unendlich sein muss. Da jedoch im Gegensatz zum vorherigen Beispiel der Koeffizient des Monoms höheren Grades im Zähler negativ ist, ist der Grenzwert positiv unendlich, d. h:
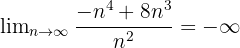
Grenzwert des Quotienten, wenn der Nenner einen höheren Grad als der Zähler hat
Wenn der Nenner einen höheren Grad hat, ist der Grenzwert 0.
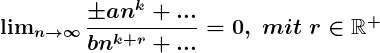
Beispiele
1 Berechne den Grenzwert von 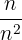 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
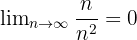
2 Berechne den Grenzwert von 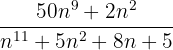 , wenn n gegen unendlich konvergiert.
, wenn n gegen unendlich konvergiert.
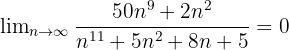
Mit KI zusammenfassen:












