Kapitel
Die Formeln für die Berechnung der Determinanten werden je nach Ordnung der Determinante angegeben. Es gibt auch eine allgemeine Methode, um die Berechnung für jede beliebige Ordnung durchzuführen.
Formeln für Determinanten
Berechnung einer Determinante der Ordnung 1
Da es sich um ein einziges Element handelt, ist die Determinante das gleiche Element
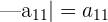
Berechnung einer Determinante der Ordnung 2
Sie kann berechnet werden, indem man das Produkt der Elemente der Diagonale vom Produkt der Elemente der Gegendiagonale subtrahiert.
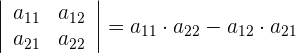
Berechnung einer Determinante der Ordnung 3
Un Eine häufig verwendete Methode ist die Regel von Sarrus, bei der die Terme mit dem Vorzeichen 
aus den Elementen der Hauptdiagonale und den Elementen der parallelen Diagonalen mit dem jeweils gegenüberliegenden Scheitelpunkt gebildet werden.
Die Terme mit dem Vorzeichen 
werden durch die Elemente der Nebendiagonale und die Elemente der Paralleldiagonalen mit dem jeweils gegenüberliegenden Scheitelpunkt gebildet.
Berechnung einer Determinante beliebiger Ordnung
Hierbei muss gewährleistet sein, dass eine der Zeilen der Determinante aus Nullelementen minus 1 besteht: dem Basiselement, das den Wert 1 oder -1 hat.
Wir führen folgende Schritte durch:
1 Wenn ein Element der Determinante den Wert 1 hat, wird eine der beiden Zeilen gewählt: die Zeile oder die Spalte, die dieses Element enthält (man muss diejenige wählen, die die größtmögliche Anzahl von Nullelementen enthält).
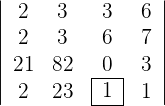
2 Wenn nicht, führen wir einen der folgenden Schritte durch:
a Wir betrachten eine Reihe, die so viele Nullelemente wie möglich enthält, und gehen so vor, dass eines der Elemente dieser Reihe entweder eine 1 oder eine -1 ist (wir befassen uns mit einer beliebigen parallelen Reihe).
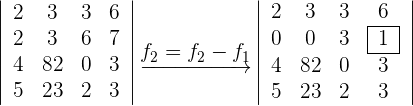
b Dividiert man die Zeile (oder die Spalte) durch eines ihrer Elemente, so muss man die Determinante mit diesem Element multiplizieren, damit sich ihr Wert nicht ändert. Das heißt, wir nehmen einen gemeinsamen Faktor in einer Zeile (oder einer Spalte) aus einem ihrer Elemente.
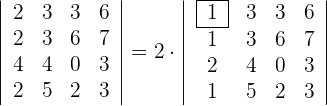
2 Wenn wir das Basiselement als Referenz nehmen, werden wir so vorgehen, dass alle Elemente der Zeile oder Spalte, in der es sich befindet, Nullen sind.
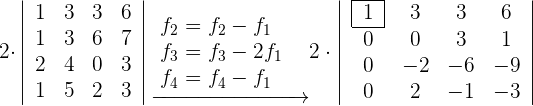
3 Wir nehmen die Adjunkte des Basiselements und erhalten so eine Determinante der Ordnung eine Einheit niedriger als das Original.
Eigenschaften von Determinanten
1 Die Determinante einer Matrix und die Determinante ihrer Transposition sind gleich.
2 Wenn die Determinante einer Matrix 0 ist, gilt:
a Sie hat zwei gleiche Zeilen (oder Spalten).
b Alle Elemente in einer Zeile (oder einer Spalte) sind 0.
c Die Elemente einer Zeile (oder einer Spalte) sind eine Linearkombination der anderen.
3 Eine dreieckige Determinante ist gleich dem Produkt der Elemente der Hauptdiagonale.
4 Wenn zwei Zeilen (oder zwei Spalten) in einer Determinante gegeneinander vertauscht werden, ändert sich nur das Vorzeichen ihres Werts.
5 Werden die Elemente einer Zeile (oder Spalte) zu den Elementen einer anderen Zeile (oder Spalte), die mit einer reellen Zahl multipliziert werden, addiert, ändert sich der Wert der Determinante nicht.
6 Wenn eine Determinante mit einer reellen Zahl multipliziert wird, wird eine beliebige Zeile (oder eine beliebige Spalte) mit dieser Zahl multipliziert, aber nur eine.
7 Wenn alle Elemente einer Zeile (oder Spalte) aus zwei Summanden bestehen, zerfällt diese Determinante in die Summe von zwei Determinanten, wobei die anderen Zeilen (oder Spalten) unverändert bleiben.
8 Die Determinante eines Produkts von Matrizen ist gleich dem Produkt ihrer Determinanten
Berechnung der inversen Matrix
Um die Inverse einer Matrix 
zu berechnen, verwenden wir folgende Formel
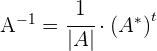
mit
Berechnung des Rangs einer Matrix
Der Rang ist die Ordnung der größten quadratischen Untermatrix, die nicht 0 ist.
Wir können eine Reihe verwerfen, wenn:
Alle ihre Koeffizienten Nullen sind.
Zwei Zeilen identisch sind.
Eine Reihe proportional zu einer anderen Reihe ist.
Eine Reihe eine Linearkombination von anderen Reihen ist.
Im Allgemeinen lauten die Schritte zur Berechnung des Rangs mittels Determinanten wie folgt:
1 Wir streichen die Zeilen (oder Spalten), die die oben genannten Bedingungen erfüllen.
2 Wenn mindestens ein Element der Matrix ungleich 0 ist, ist ihre Determinante nicht 0 und der Rang ist daher größer oder gleich 1.
3 Der Rang ist größer oder gleich 2, wenn es eine quadratische Untermatrix der Ordnung 2 gibt, deren Determinante ungleich 0 ist.
4 Der Rang ist größer oder gleich 3, wenn es eine quadratische Untermatrix der Ordnung 3 gibt, deren Determinante ungleich 0 ist.
5 Der Rang ist größer oder gleich 4, wenn es eine quadratische Untermatrix der Ordnung 4 gibt, deren Determinante ungleich 0 ist.
Auf die gleiche Weise wird geprüft, ob ihr Rang größer als 4 ist, bis die höchstmögliche Untermatrix (oder Untermatrizen) eine Determinante von 0 hat (oder haben).
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
