Fundamentalsatz der Analysis
Der Fundamentalsatz der Analysis (oder auch Hauptsatz der Differential- und Integralrechnung (HDI)) besagt, dass die Ableitung des Integrals 
der stetigen Funktion 
die Funktion ist.
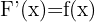
Der Fundamentalsatz der Analysis besagt, dass die Ableitung und die Integration inverse Operationen sind.
Durch die Integration einer stetigen Funktion und ihre anschließende Ableitung wird die ursprüngliche Funktion wiederhergestellt.
Beispiel:
Berechne die Ableitung von
1 Wir stellen fest, dass 
, weshalb ihr Differential 
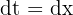ist
2 Wir wenden den Fundamentalsatz der Analysis an und erhalten
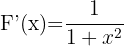
Beispiel:
Berechne die Ableitung von
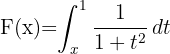
1 Zunächst ändern wir die Integrationsgrenzen, was dazu führt, dass sich das Vorzeichen des Integrals ändert.
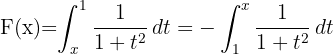
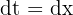2 Wir stellen fest, dass , weshalb ihr Differential ist
3 Wir wenden den Fundamentalsatz der Analysis an und erhalten
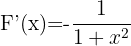
Beispiel:
Berechne die Ableitung von
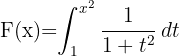
1 Wir stellen fest, dass 
, weshalb ihr Differential 
ist
2 Wir wenden den Fundamentalsatz der Analysis an und erhalten
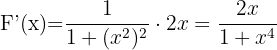
Mittelwertsatz der Differentialrechnung für Integrale
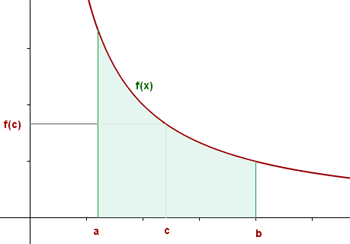
Wenn eine Funktion auf einem geschlossenen Intervall 
stetig ist, dann gibt es einen Punkt 
im Inneren des Intervalls, so dass:
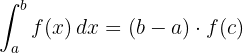
Beispiel:
Berechne den Wert von des Mittelwertsatzes für die Funktion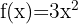 
auf dem Intervall 
.
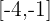1 Wir berechnen das Ergebnins des bestimmten Integrals
2 Da die Funktion auf dem Intervall 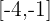stetig ist, kann der Mittelwertsatz angewendet werden.
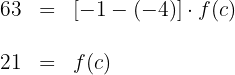
3 Wir setzen den Wert von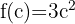 
in die vorherige Gleichung ein und bestimmen
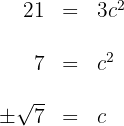
Die positive Lösung ist nicht gültig, da sie nicht Teil des Intervalls ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
