
1 Wir trennen die Terme des Zählers, die jeweils einen gemeinsamen Nenner haben, und wenden die Regel des Integrals für Additionen an

2 Wir integrieren jedes der erhaltenen Integrale und nutzen dazu die Formeln
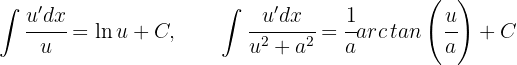
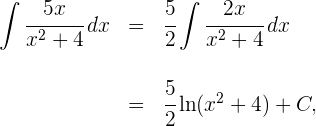
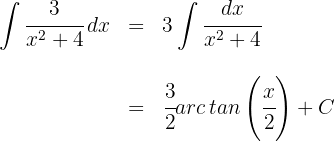
3 Somit ist das Ergebnis des Integrals
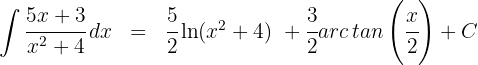
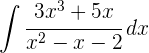
1 Wir schreiben den Quotienten in der Form 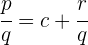 , wobei
, wobei  der Quotient ist und
der Quotient ist und  der Rest
der Rest
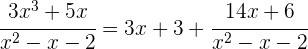
2 Wir schreiben das Integral

3 Wir lösen das Integral
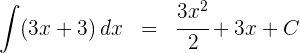
4 Wir lösen das 2. Integral mit der Partialbruchzerlegung

Wir addieren:
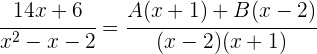
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:

Um die Werte von 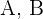 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren

Wir berechnen die Integrale der einfachen Brüche:
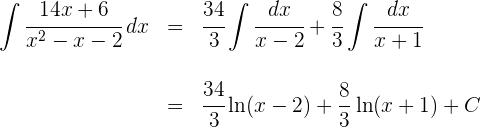
5 Somit ist die Lösung des Integrals
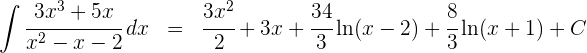
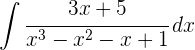
1 Wir faktorisieren den Quotienten

2 Wir lösen mit der Partialbruchzerlegung
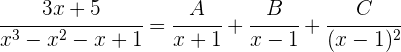
Wir addieren:
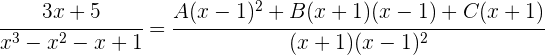
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
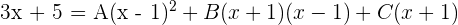
Um die Werte von 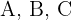 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren
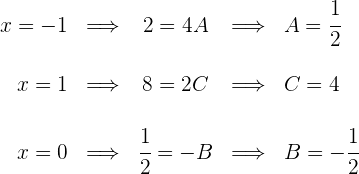
3 Wir berechnen die Integrale der einfachen Brüche:
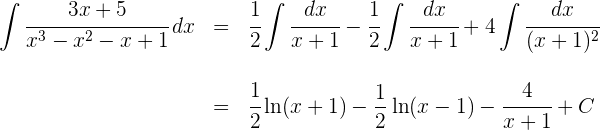
4 Somit ist die Lösung des Integrals
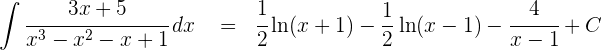

1 Wir lösen mit der Partialbruchzerlegung
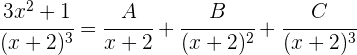
Wir addieren:
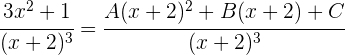
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
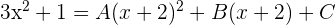
Um die Werte von 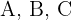 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren

Wir leiten ab und substituieren 

Wir leiten erneut ab

2 Wir berechnen die Integrale der einfachen Brüche:
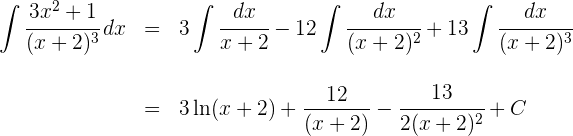
3 Somit ist die Lösung des Integrals


1 Wir faktorisieren den Quotienten
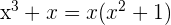
2 Wir lösen mit der Partialbruchzerlegung

Wir addieren:

Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
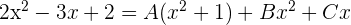
Um die Werte von 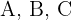 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren

Wir leiten ab und substituieren erneut 
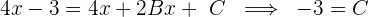
Wir leiten noch einmal ab
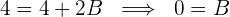
3 Wir berechnen die Integrale der einfachen Brüche:
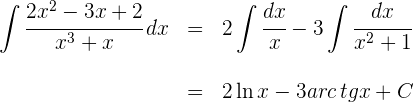
4 Somit ist die Lösung des Integrals
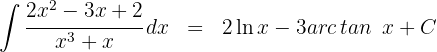
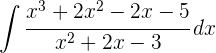
1 Wir drücken den Quotienten in der Form 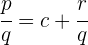 aus, wobei
aus, wobei  der Quotient und
der Quotient und  der Rest ist
der Rest ist
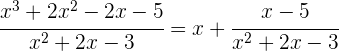
2 Wir schreiben das Integral
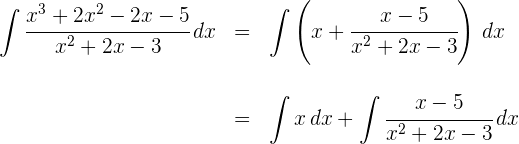
3 Wir lösen das 1. Integral

Wir faktorisieren den Quotienten

Wir lösen mit der Partialbruchzerlegung

Wir addieren:

Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:

Um die Werte von 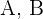 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren
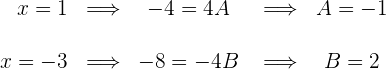
4 Wir berechnen die Integrale der einfachen Brüche:

5 Somit ist die Lösung des Integrals

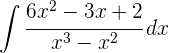
1 Wir faktorisieren den Quotienten
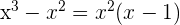
2 Wir lösen mit der Partialbruchzerlegung
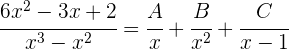
Wir addieren:
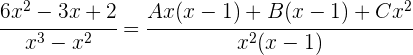
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:

Um die Werte von 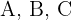 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren
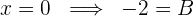
Wir leiten ab und substituieren erneut 
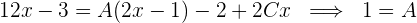
Wir leiten erneut ab

3 Wir berechnen die Integrale der einfachen Brüche:
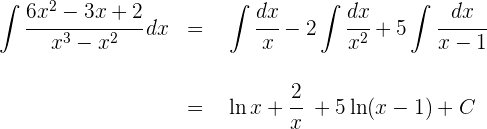
4 Somit ist die Lösung des Integrals
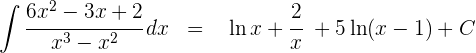

1 Wir lösen mit der Partialbruchzerlegung
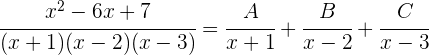
Wir addieren:
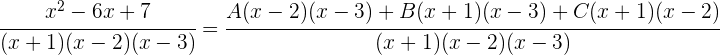
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
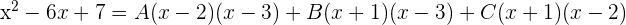
Um die Werte von 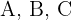 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren
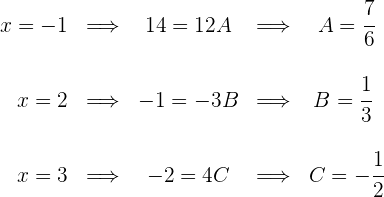
2 Wir berechnen die Integrale der einfachen Brüche:
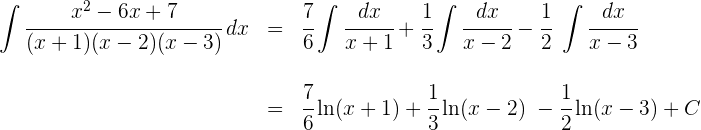
3 Somit ist die Lösung des Integrals


1 Wir lösen mit der Partialbruchzerlegung
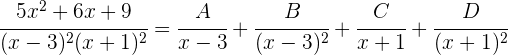
Wir addieren:

Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
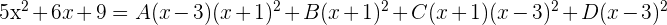
Um die Werte von 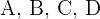 zu berechnen, weisen wir
zu berechnen, weisen wir  die Werte zu, für die der Nenner 0 wird und einen weiteren
die Werte zu, für die der Nenner 0 wird und einen weiteren
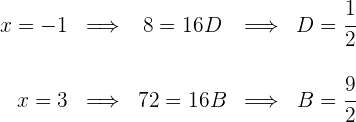
Wir leiten ab und weisen  Werte zu, für die der Nenner 0 wird
Werte zu, für die der Nenner 0 wird
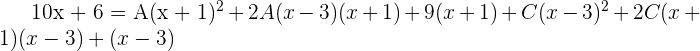

2 Wir berechnen die Integrale der einfachen Brüche:
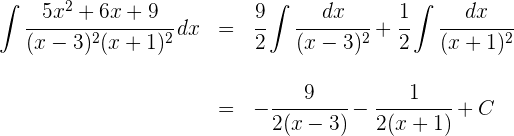
3 Somit ist die Lösung des Integrals
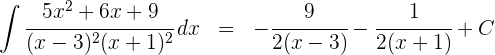
Mit KI zusammenfassen:


