Kapitel
Eine Folge ist eine Menge von Zahlen, die nacheinander angeordnet sind:
Die Zahlen 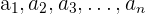 ; heißen Glieder einer Folge.
; heißen Glieder einer Folge.
Der tiefgestellte Index gibt den Platz an, den das Glied in der Folge einnimmt.
Das allgemeine Glied  ist ein Kriterium, mit dem wir ein beliebiges Glied der Folge bestimmen können.
ist ein Kriterium, mit dem wir ein beliebiges Glied der Folge bestimmen können.

Grenzwerte einer Folge
Endlicher Grenzwert
Eine Folge  hat dann und nur dann den Grenzwert
hat dann und nur dann den Grenzwert  , wenn für jede positive Zahl
, wenn für jede positive Zahl  ,
,
die wir nehmen, ein Glied  existiert, von dem aus alle Glieder von
existiert, von dem aus alle Glieder von  , die auf
, die auf
 folgen, folgende Bedingung erfüllen:
folgen, folgende Bedingung erfüllen:
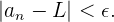
Das heißt, 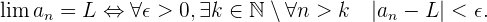
Wir können den Grenzwert einer Folge auch mithilfe von Umgebungen definieren:
Eine Folge  hat dann und nur dann den Grenzwert
hat dann und nur dann den Grenzwert  , wenn es für jede Umgebung von
, wenn es für jede Umgebung von  ,
,
die wir nehmen, egal wie klein ihr Radius  ist, ein Glied der Folge gibt, von dem ausgehend
ist, ein Glied der Folge gibt, von dem ausgehend
die folgenden Glieder zur besagten Umgebung gehören.
Wenn 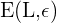 eine Umgebung von
eine Umgebung von  mit dem Radius
mit dem Radius  darstellt, gilt
darstellt, gilt 
Unendlicher Grenzwert
Eine Folge  hat den Grenzwert
hat den Grenzwert  , wenn für alle
, wenn für alle 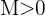
ein Glied  existiert, von dem aus alle Glieder von
existiert, von dem aus alle Glieder von  , die auf
, die auf  folgen, folgende Bedingung erfüllen:
folgen, folgende Bedingung erfüllen:
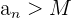 .
.
x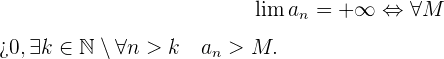
Eine Folge  hat den Grenzwert
hat den Grenzwert  , wenn für alle
, wenn für alle 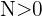
ein Glied  existiert, von dem aus alle Glieder von
existiert, von dem aus alle Glieder von  , die auf
, die auf  folgen, folgende Bedingung erfüllen:
folgen, folgende Bedingung erfüllen:
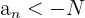 .
.
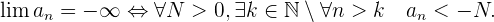
Eigenschaften von Grenzwerten
Die folgende Liste beschreibt die gängigsten Eigenschaften von Grenzwerten
1 Wenn ein Grenzwert existiert, dann ist er eindeutig.
2 Wenn eine Folge  einen Grenzwert hat, haben alle Teilfolgen denselben Grenzwert wie
einen Grenzwert hat, haben alle Teilfolgen denselben Grenzwert wie  .
.
3 Alle konvergenten Folgen sind beschränkt.
4 Es gibt beschränkte Folgen, die nicht konvergent sind.
5 Alle monotonen und beschränkten Folgen sind konvergent.
6 Es gibt konvergente Folgen, die nicht monoton sind.
Infinitesimalzahl
Eine Folge  ist eine Infinitesimalzahl, wenn ihr Grenzwert 0 ist.
ist eine Infinitesimalzahl, wenn ihr Grenzwert 0 ist.
Die folgende Liste beschreibt die üblichen Eigenschaften von Infinitesimalzahlen
Eigenschaften:
1 Die Summe von zwei Infinitesimalzahlen ergibt eine Infinitesimalzahl.
2 Das Produkt aus einer Infinitesimalzahl und einer beschränkten Folge ist eine Infinitesimalzahl.
3 Das Produkt aus Infinitesimalzahlen ist eine Infinitesimalzahl.
4 Das Produkt aus einer Konstante und einer Infinitesimalzahl ist eine Infinitesimalzahl.
5 Wenn eine Folge  gegen
gegen  konvergiert, ist die Folge
konvergiert, ist die Folge  eine Infinitesimalzahl.
eine Infinitesimalzahl.
6 Wenn eine Folge  divergent ist, ist ihre Umkehrung eine Infinitesimalzahl.
divergent ist, ist ihre Umkehrung eine Infinitesimalzahl.
Rechnen mit Grenzwerten
Im Folgenden siehst du die gängisten Rechenoperationen mit Grenzwerten
1 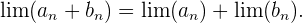
2 
3 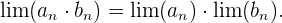
4 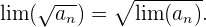
5 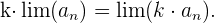
6 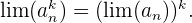
8 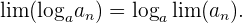
Bei der Anwendung dieser Rechenregeln können die folgenden Fälle auftreten:
Es ist zu beachten, dass die von uns verwendeten symbolischen Ausdrücke nicht exakte
Gleichheiten sind, da Unendlich keine reelle Zahl ist, sondern eine Form, um
Ergebnisse auszudrücken.
1 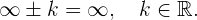
2 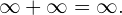
3 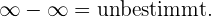
4 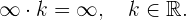
5 
6 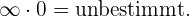
7 
8 
9 
10 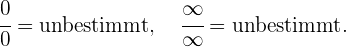
11 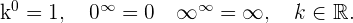
12 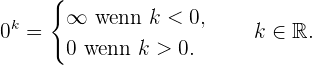
13 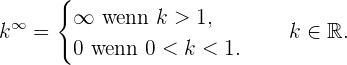
14 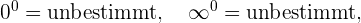
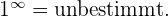
Eine Folge bestimmen
Eine Folge kann auf zwei verschiedene Arten bestimmt werden, die im Folgenden vorgestellt werden.
Durch das allgemeine Glied
Wir können eine allgemeine Formel für das  -te Glied
-te Glied  einer Folge bestimmen. Zum Beispiel
einer Folge bestimmen. Zum Beispiel
für die Folge
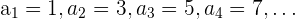 ist das allgemeine Glied
ist das allgemeine Glied 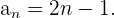
Rekursion
Die Glieder können anhand der vorhergehenden Glieder ermittelt werden. Zum Beispiel:
Für die Folge 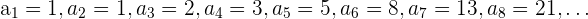
haben wir 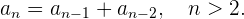
Rechnen mit Folgen
Gegeben sind die Folgen  ,
,  und
und  . Wir können folgende Regeln festlegen:
. Wir können folgende Regeln festlegen:

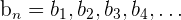
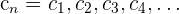
Folgen addieren
Die Addition von Folgen wird Glied für Glied durchgeführt 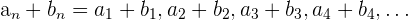
Rechenregeln
Wie bei der üblichen Addition von Zahlen gelten auch für die Addition von Folgen folgende Regeln
1 Assoziativität:
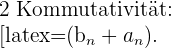
3 Neutrales Element:
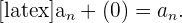
4 Gegenfolge:
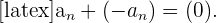
Subtraktion von Folgen
Die Subtraktion von Folgen erfolgt Glied für Glied 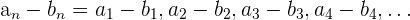
Multiplikation von Folgen
Die Multiplikation von Folgen erfolgt Glied für Glied 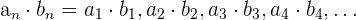
Rechenregeln
Wie für das gewöhnliche Produkt von Zahlen gelten auch für das Produkt von Folgen die folgenden Eigenschaften
1 Assoziativität:

2 Kommutativität:
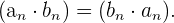
3 Neutrales Element:
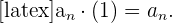
4 Umkehrfolge
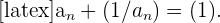
5 Distributivität in Bezug auf die Summe
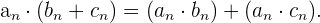
Inverse Folge
Eine Folge ist invers, wenn alle ihre Glieder ungleich
0 sind. Wenn die Folge  invers ist, gilt:
invers ist, gilt:
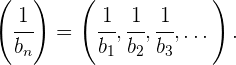
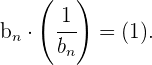
Quotient
Der Quotient aus zwei Folgen kann nur ermittelt werden, wenn der Nenner
invers ist.
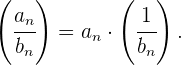
Arten von Folgen
Monotone Folgen
Das folgende Diagramm zeigt alle Arten von monotonen Folgen, die vorkommen können
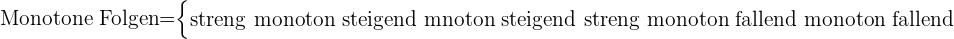
Streng monoton steigende Folgen
Eine Folge ist streng monoton steigend, wenn jedes Glied größer oder gleich dem vorhergehenden Glied ist.

Monton steigende Folgen
Eine Folge ist monton steigend, wenn jedes Glied größer oder gleich dem vorhergehenden Glied ist.
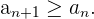
Streng monoton fallende Folgen
Eine Folge ist streng monoton fallend, wenn jedes Glied der Folge kleiner als das vorhergehende Glied ist.
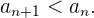
Monton fallende Folgen
Eine Folge ist monoton fallend, wenn jedes Glied kleiner oder gleich dem vorhergehenden Glied ist.
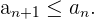
Konstante Folgen
Eine Folge ist konstant, wenn alle ihre Glieder gleich einer
Konstante  sind. Das heißt,
sind. Das heißt, 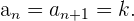
Nach unten beschränkte Folgen
Eine Folge ist nach unten beschränkt, wenn alle ihre Glieder größer oder
gleich einer bestimmten Zahl  sind, die wir untere Schranke der Folge nennen.
sind, die wir untere Schranke der Folge nennen.

Die größte untere Schranke wird Infimum genannt .
Wenn das Infimum einer Folge eines ihrer Glieder ist, nennt man es Minimum.
Die gesamte nach unten beschränkte Folge ist monoton steigend.
Nach oben beschränkte Folgen
Eine Folge ist nach oben beschränkt, wenn alle ihre Glieder kleiner oder
gleich einer bestimmten Zahl 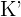 sind, die wir obere Schranke der Folge nennen.
sind, die wir obere Schranke der Folge nennen.
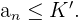
Die kleinste obere Schranke wird Supremum genannt.
Wenn das Supremum einer Folge eines ihrer Glieder ist, nennt man es Maximum.
Die gesamte nach oben beschränkte Folge ist monton fallend.
Beschränkte Folgen
Eine Folge gilt als beschränkt, wenn sie nach oben und unten beschränkt ist. Das heißt:
Es gibt eine Zahl  kleiner oder gleich aller Glieder der Folge und eine weitere Zahl
kleiner oder gleich aller Glieder der Folge und eine weitere Zahl 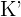
größer oder gleich aller Glieder der Folge. Daher liegen alle
Glieder der Folge zwischen  und
und 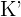 .
.

Konvergente Folgen
Haben einen endlichen Grenzwert.
Divergente Folgen
Sie haben einen unendlichen Grenzwert oder
oder  .
.
Oszillierende Folgen
Sie sind weder konvergent noch divergent. Ihre Glieder wechseln von der höchsten zur niedrigsten Zahl
oder umgekehrt. Zum Beispiel 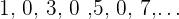
Alternierende Folgen
Das Vorzeichen ihrer Glieder wechselt sich ab.
Arithmetische Folgen
Eine arithmetische Folge ist eine Folge von Zahlen, die so beschaffen ist, dass jede von ihnen (außer der ersten) gleich der vorhergehenden Zahl plus einer festen Zahl ist.
Diese wird Differenz genannt
und mit  dargestellt.
dargestellt.
Allgemeines Glied einer arithmetischen Folge
Für eine Folge dieser Art gibt es die folgenden Arten von allgemeinen Gliedern
1 Das Anfangsglied ist bekannt.
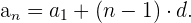
2 Wenn wir den Wert kennen, den ein beliebiges anderes Glied der Folge hat.

Interpolation von Gliedern
Die Interpolation von Differenz- oder arithmetischen Mitteln zwischen zwei Zahlen bedeutet das Erstellen einer
arithmetischen Folge, die als Extrema die gegebenen Zahlen hat.
Gegeben sind  und
und  sowie die Anzahl der zu interpolierenden Mittelwerte
sowie die Anzahl der zu interpolierenden Mittelwerte  .
.
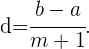
Summe von äquidistanten Gliedern
Wenn 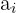 und
und  zwei äquidistante Glieder zu den Extrema sind, gilt, dass die Summe
zwei äquidistante Glieder zu den Extrema sind, gilt, dass die Summe
der äquidistanten Glieder gleich der Summe der Extrema ist.
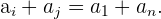
Gegeben ist die Folge 
Es gilt: 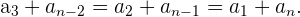
Summe von n aufeinanderfolgenden Gliedern
Die Summe von  einer arithmetischen Folge erhält man unter Verwendung der folgenden Formel
einer arithmetischen Folge erhält man unter Verwendung der folgenden Formel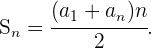
Geometrische Folgen
Eine geometrische Folge ist eine Folge, bei der jedes Glied ermittelt werden kann,
indem man das vorhergehende Glied mit einer bestimmten Menge 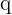 , Quotient genannt, multipliziert.
, Quotient genannt, multipliziert.
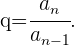
Allgemeines Glied einer geometrischen Folge
Für eine Folge dieser Art haben wir die folgenden Arten des allgemeines Glieds
1 Das Anfangsglied ist bekannt.
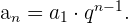
2 Wir kennen den Wert, den ein beliebiges anderes Glied der Folge annimmt.
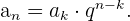
Interpolation von Gliedern
Die Interpolation von geometrischen oder proportionalen Mittel bedeutet das Erstellen
einer geometrischen Folge, die als Extrema die gegebenen Zahlen hat.
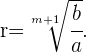
Summe von n aufeinanderfolgenden Gliedern
Die Summe von  aufeinanderfolgenden
aufeinanderfolgenden  einer geometrischen Folge ergibt sich aus folgender Formel
einer geometrischen Folge ergibt sich aus folgender Formel 
Summe der Glieder einer abnehmenden geometrischen Folge
Für den Fall einer abnehmenden geometrischen Folge haben wir folgende Formel 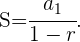
Produkt aus zwei äquidistanten Gliedern
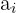 und
und  sind zwei äquidistante Glieder zu den Extrema. Es gilt, dass das
sind zwei äquidistante Glieder zu den Extrema. Es gilt, dass das
Produkt der äquidistanten Glieder gleich dem Produkt der Extrema ist.
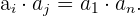
Gegeben ist die Folge 
Es gilt: 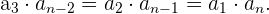
Produkt aus n äquidistanten Gliedern
Im Falle von äquidistanten Gliedern ist das Produkt gegeben durch 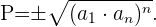
Allgemeines Glied einer Folge
1 Überprüfe, ob es sich um eine arithmetische Folge handelt.
2 Überprüfe, ob es sich um eine geometrische Folge handelt.
3 Überprüfe, ob die Glieder Quadratzahlen sind.
Wir können allerdings auch auf Folgen stoßen, deren Glieder Zahlen sind,
die sich Quadratzahlen annähern.
4 Wenn die Glieder der Folge nacheinander das Vorzeichen wechseln.
Wenn die ungeraden Glieder negativ und die geraden Glieder positiv sind: Wir multiplizieren
 por
por  .
.
Wenn die ungeraden Glieder positiv und die geraden Glieder sind: Wir multiplizieren
 por
por 
5 Wenn die Glieder der Folge Brüche sind:
Das allgemeine Glied wird für den Zähler und den Nenner separat berechnet.
Untersuchung von Unbestimmtheiten
Unendlich geteilt durch Unendlich
Dies hat die folgende Form
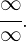
Lösung: Jeder Summand wird durch die Potenz mit dem höchsten Exponenten dividiert.
Praktische Regel
1 Wenn der Zähler und der Nenner denselben Grad haben, ist der Grenzwert
der Quotient aus den Koeffizienten der Potenzen höheren Grades.
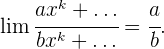
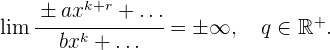
2 Wenn der Nenner einen höheren Grad hat, ist der Grenzwert 0.
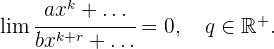
Unendlich minus Unendlich
Es wird wie folgt dargestellt 
1. Ganzzahlige Folge
Der gemeinsame Faktor wird aus der Potenz mit dem höchsten Exponenten ausgeklammert.
Praktische Regel:
Der Grenzwert ist  , abhängig vom Vorzeichen des Koeffizienten mit dem höchsten Grad.
, abhängig vom Vorzeichen des Koeffizienten mit dem höchsten Grad.
2. Rationale Folgen.
Wir bringen auf einen gemeinsamen Nenner und wenn wir  erhalten, lösen wir die
erhalten, lösen wir die
Unbestimmtheit.
3. Irrationale Folgen.
Wir multiplizieren oder dividieren.
Null mal Unendlich
Es wird wie folgt dargestellt 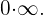
Es wird in  umgewandelt.
umgewandelt.
Wir wenden die folgende Gleichheit an 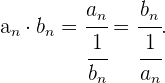
Null geteilt durch Null
Es wird wie folgt dargestellt 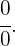
Und wird in  umgeformt
umgeformt
Eins hoch Unendlich
Es wird wie folgt dargestellt 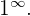
Wir lösen, indem wir den Ausdruck in eine Potenz der Zahl e umwandeln.
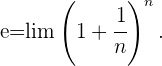
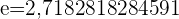
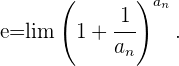
1. Methode
Wir addieren und subtrahieren 1 zu/von der Basis.
Wir bringen die letzten Summanden auf einen gemeinsamen Nenner.
Wir substituieren mit dem Kehrwert des Kehrwerts.
Wir heben den Nenner auf seinen Kehrwert.
2. Methode
Diese Unbestimmtheit wird durch die folgende Gleichheit gelöst 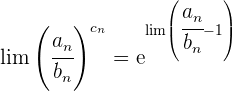
Mit KI zusammenfassen:












