Kapitel
Unendlich ist keine Zahl. Rechenoperationen, die wir mit  durchführen, sind lediglich ein Hilfsmittel, das uns bei der Lösung von Grenzwerten hilft.
durchführen, sind lediglich ein Hilfsmittel, das uns bei der Lösung von Grenzwerten hilft.

Aufgben zu Folgen
Aufgaben zu Grenzwerten von Folgen der Form 
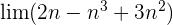

Wir faktorisieren 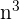 :
:



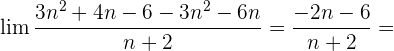
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 
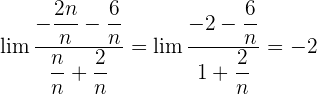
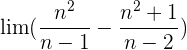

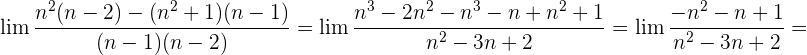
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 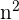

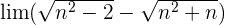
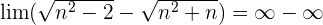
Multiplikation und Division durch das konjugierte Binom
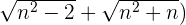
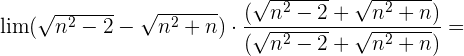
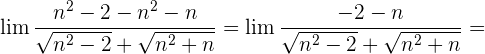
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 

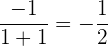
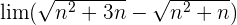
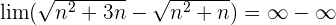

Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 
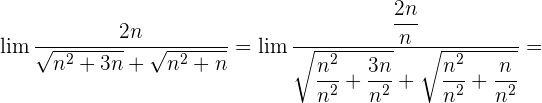
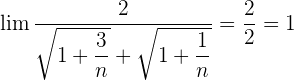
Aufgaben zu Grenzwerten von Folgen der Form 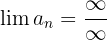
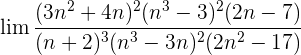
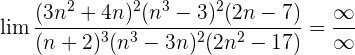
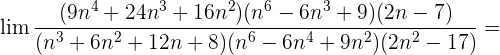
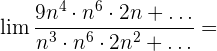
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 

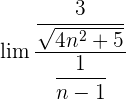

Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch  . Denke daran, dass das
. Denke daran, dass das  innerhalb der Wurzel zu
innerhalb der Wurzel zu 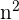 wird.
wird.
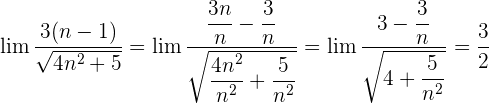
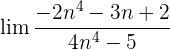
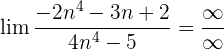
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 

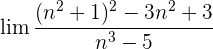
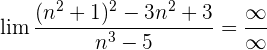
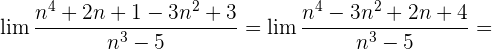 Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 
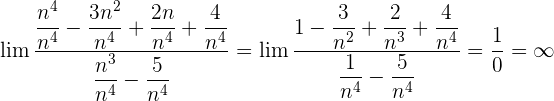

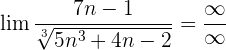
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch  . Denke daran, dass das
. Denke daran, dass das  innerhalb der Kubikwurzel zu
innerhalb der Kubikwurzel zu 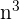 wird
wird
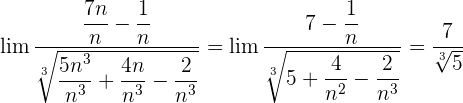
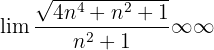

Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 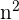 . Denke daran, dass das
. Denke daran, dass das 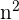 innerhalb der Wurzel zu
innerhalb der Wurzel zu  wird
wird



Wir separieren 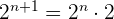 und
und 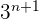 . Im Anschluss dividieren wir durch
. Im Anschluss dividieren wir durch 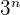
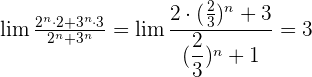
Aufgaben zu Grenzwerten von Folgen der Form  und
und 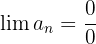

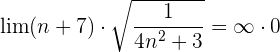
Wir stellen den 1. Faktor unter die Wurzel und erhalten 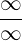 .
.
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 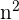
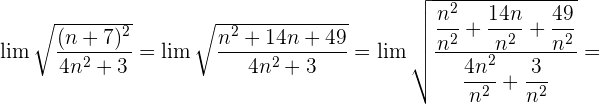
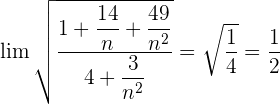
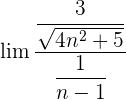
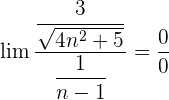
Wir wandeln um: 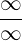 .
.
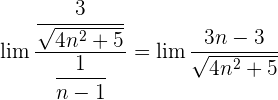
Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch  . Denke daran, dass das
. Denke daran, dass das  innerhalb der Wurzel zu
innerhalb der Wurzel zu 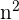 wird
wird



Wir wandeln um: 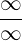 .
.

Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 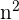

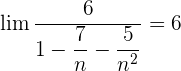
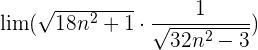
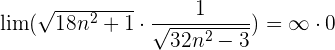
Wir wandeln um: 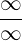 .
.

Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 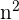
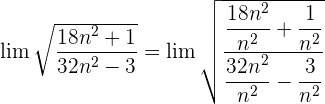


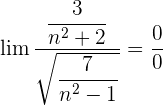
Wir wandeln um: 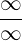 . Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch
. Wir dividieren jeden Faktor sowohl des Zählers als auch des Nenners durch 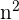 . Denke daran, dass das
. Denke daran, dass das 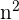 innerhalb der Wurzel zu
innerhalb der Wurzel zu  wird.
wird. 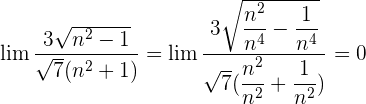
Aufgaben zu Grenzwerten von Folgen der Form 
Für diese Aufgaben müssen wir folgende Regeln beachten:
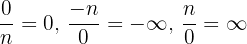 .
.
 ist hierbei eine beliebige positive Zahl.
ist hierbei eine beliebige positive Zahl.

Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 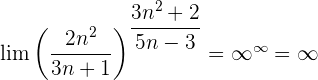
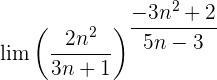
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 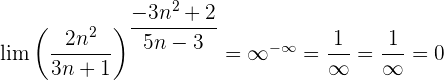

Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 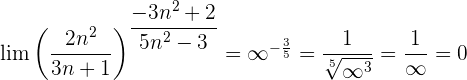
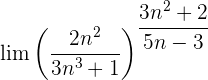
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 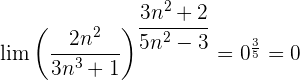
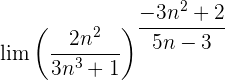
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 
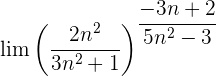
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 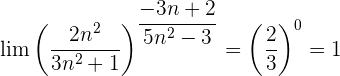
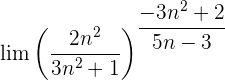
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 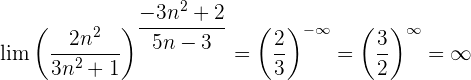
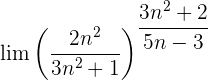
Wir werten direkt sowohl den Grenzwert der Potenz als auch den Grenzwert der Basis aus: 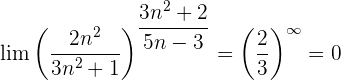
Aufgaben zu Grenzwerten von Folgen der Form 
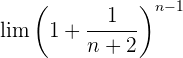
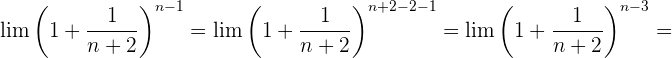

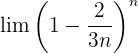
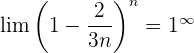

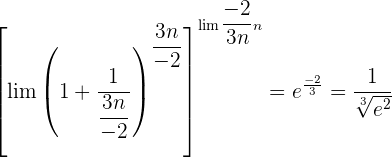
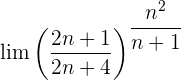
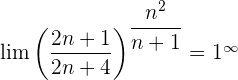
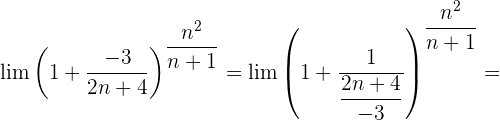
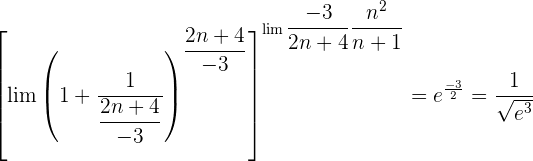
Aufgaben zu Grenzwerten von arithmetischen und geometrischen Folgen
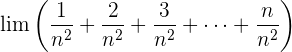
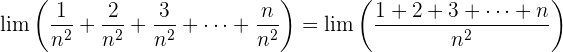
Der Zähler ist die Summe der Glieder einer arithmetischen Folge. 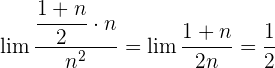
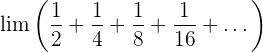
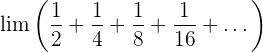
Wir haben die Summe von unendlich vielen Termen einer geometrischen Folge.

Aufgaben zu Grenzwerten von Wurzelfolgen

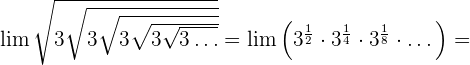
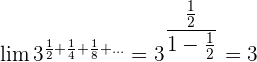
In dieser Aufgabe wenden wir im vorletzten Schritt die Formel der unendlichen geometrischen Folge an.
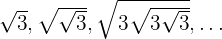
Wir stellen fest, dass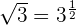

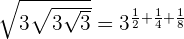 Entonces
Entonces

Der Exponent ist die unbegrenzte Summe einer abnehmenden geometrischen Folge:
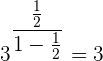
Mit KI zusammenfassen:












