Kapitel
Willkommen zu dieser Reihe von Übungen zur statistischen Inferenz. Die statistische Inferenz ist ein grundlegendes Instrument der Datenanalyse, das es uns ermöglicht, Schlussfolgerungen zu ziehen und Entscheidungen über Populationen oder Phänomene auf der Grundlage begrenzter Stichproben von Informationen zu treffen. Anhand dieser Übungen lernen wir, wie man statistische Methoden einsetzt, um Schätzungen vorzunehmen, Entscheidungen zu treffen und die Zuverlässigkeit der Ergebnisse zu bewerten.
Während dieser Reihe von Übungen arbeiten wir mit Schlüsselkonzepten wie Konfidenzintervallen, Hypothesentests und Signifikanzanalysen, die es uns ermöglichen, Schlussfolgerungen zu ziehen, die durch Beweise aus unseren Daten gestützt werden. Im weiteren Verlauf werden wir lernen, wie wir unsere Ergebnisse interpretieren und die Schlussfolgerungen, die wir daraus ziehen, effektiv kommunizieren können.

Stichprobe
In einer Fabrik mit 600 Beschäftigten wollen wir eine Stichprobe von 20 Beschäftigten nehmen. Wir wissen, dass es 200 Beschäftigte in Abteilung A, 150 in Abteilung B, 150 in Abteilung C und 100 in Abteilung D gibt.
Wenn beschlossen wird, eine geschichtete Stichprobe mit proportionaler Schichtung einzusetzen, wie groß wird jede Schicht sein?
 ist hierbei der Umfang der Grundgesamtheit und
ist hierbei der Umfang der Grundgesamtheit und  der Umfang der Stichprobe. Analog dazu ist
der Umfang der Stichprobe. Analog dazu ist 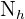 der Umfang der Schicht
der Umfang der Schicht  und
und  der Umfang der Stichprobe, den wir aus
der Umfang der Stichprobe, den wir aus  nehmen. Wenn wir also eine proportionale Schichtung haben, gilt
nehmen. Wenn wir also eine proportionale Schichtung haben, gilt
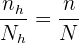
Das Problem besteht lediglich darin, die Werte  für jede Schicht zu ermitteln. Und da der Umfang der Grundgesamtheit
für jede Schicht zu ermitteln. Und da der Umfang der Grundgesamtheit 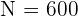 ist:
ist: 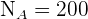 ,
, 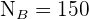 ,
, 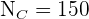 und
und 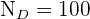 .
.
Außerdem kennen wir  , sodass wir alle Daten haben, um den Stichprobenumfang für jede Schicht zu berechnen. Wir bestimmen zunächst
, sodass wir alle Daten haben, um den Stichprobenumfang für jede Schicht zu berechnen. Wir bestimmen zunächst  :
:
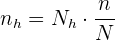
Für Abteilung A gilt:

Für Abteilung B:
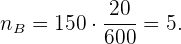
Für Abteilung C:
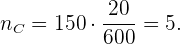
Und schließlich für Abteilung D:

Wir überprüfen

Eine bestimmte Einkaufszentrumskette beschäftigt 150 Personen in der Personalabteilung, 450 in der Verkaufsabteilung, 200 in der Buchhaltung und 100 im Kundendienst. Für die Durchführung einer Umfrage soll eine Stichprobe von 180 Mitarbeitenden ausgewählt werden.
a Welche Art von Stichprobe sollten wir für die Auswahl der Stichprobe verwenden, wenn wir wollen, dass sie Mitarbeitende aus den vier oben genannten Abteilungen umfasst?
b Wie viele Mitarbeitende müssten wir in jeder Abteilung auswählen, wenn wir eine proportionale Schichtung nutzen?
a Die geschichtete Zufallsstichprobe (mit oder ohne proportionaler Schichtung) ist die einzige Möglichkeit, die garantiert, dass Mitarbeitende aus allen vier Abteilungen dabei sind.
b Die Vorgehensweise ist ähnlich wie bei den vorherigen Übungen. Der Umfang der Grundgesamtheit ist
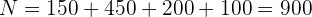
und der Umfang der Stichprobe ist 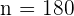 . Die Anzahl der Mitarbeitenden in der Personalabteilung, die wir wählen müssen, ist also
. Die Anzahl der Mitarbeitenden in der Personalabteilung, die wir wählen müssen, ist also
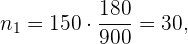
die Anzahl der Mitarbeitenden in der Verkaufsabteilung ist
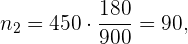
die Anzahl der Mitarbeitenden in der Buchhaltung ist

und die Anzahl der Mitarbeiter, die wir aus der Kundendienstabteilung nehmen müssen, ist

In einer bestimmten Bildungseinrichtung gibt es 100 Lehrkräfte, 95 Verwaltungsangestellte und 505 Schüler*innen. Es wird eine Stichprobe von 30 Personen gebildet. Wie viele Personen müssten wir in jeder Gruppe auswählen, wenn wir eine proportionale Schichtung anwenden?
Der Umfang der Grundgesamtheit ist
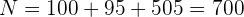
und der Stichprobenumfang ist 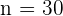 . Die Anzahl der Personen in der Gruppe der auszuwählenden Lehrkräfte ist also
. Die Anzahl der Personen in der Gruppe der auszuwählenden Lehrkräfte ist also
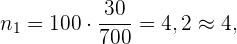
die Anzahl der Mitarbeitenden in der Verwaltung ist
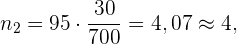
die Anzahl der Schüler*innen ist
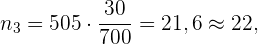
Stichprobenwahrscheinlichkeit
Bist du auf der Suche nach Nachhilfe in Algebra? Finde deinen Profi bei Superprof!
Sieh dir folgende Grundgesamtheit an:  .
.
a Schreibe alle möglichen Stichproben der Größe zwei auf, die durch eine einfache Zufallsstichprobe ohne Ersatz ausgewählt werden.
b Berechne die Varianz der Grundgesamtheit.
c Berechne die Varianz der Stichprobenmittelwerte bei einem Stichprobenumfang von zwei.
a Die möglichen Stichproben sind alle möglichen Teilmengen der Grundgesamtheit. Das heißt:

b Um die Varianz zu berechnen, müssen wir zunächst den Mittelwert der Grundgesamtheit ermitteln:

Somit ist die Varianz
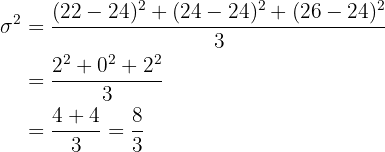
c Wir denken daran, dass die möglichen Mittelwerte als eine weitere Grundgesamtheit betrachtet werden können. Da die möglichen Stichproben  und
und  sind, haben wir drei mögliche Stichprobenmittelwerte:
sind, haben wir drei mögliche Stichprobenmittelwerte:
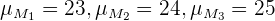
Das heißt, die Grundgesamtheit der Stichprobenmittelwerte (bei Stichprobenumfang zwei) ist
 .
.
Wir müssen die Varianz von  berechnen. Hierzu berechnen wir zunächst den Mittelwert:
berechnen. Hierzu berechnen wir zunächst den Mittelwert:

Deshalb ist die Varianz
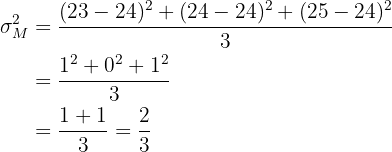
Die Varianz der Mittelwerte ist kleiner als die Varianz der ursprünglichen Grundgesamtheit.
Sieh dir folgende Grundgesamtheit an:  .
.
a Schreibe alle möglichen Stichproben des Umfangs zwei auf, die durch einfache Zufallsstichproben mit Ersatz ausgewählt werden.
b Berechne die Varianz der Grundgesamtheit.
c Berechne die Varianz der Stichprobenmittelwerte bei einem Stichprobenumfang von zwei.
a Die möglichen Stichproben sind alle möglichen Teilmengen der Grundgesamtheit. Das heißt:
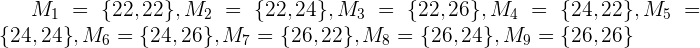
b Um die Varianz zu berechnen, müssen wir zunächst den Mittelwert der Grundgesamtheit berechnen:

Somit ist die Varianz
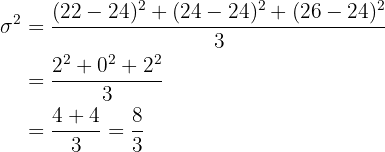
c Wir müssen daran denken, dass die möglichen Mittelwerte als eine weitere Grundgesamtheit betrachtet werden können. Da die möglichen Stichproben 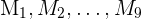 sind, haben wir neun mögliche Stichprobenmittelwerte:
sind, haben wir neun mögliche Stichprobenmittelwerte:
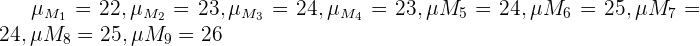
Das heißt, die Grundgesamtheit der Stichprobenmittelwerte (Stichprobenumfang zwei) ist
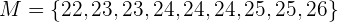
Wir müssen die Varianz von  berechnen. Hierzu berechnen wir zunächst ihren Mittelwert:
berechnen. Hierzu berechnen wir zunächst ihren Mittelwert:
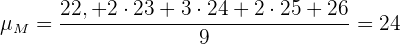
Deshalb ist die Varianz
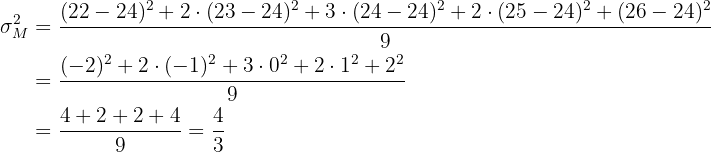
Die Varianz der Mittelwerte ist kleiner als die Varianz der Grundgesamtheit.
Die Größe der Schülerinnen einer Sprachenschule folgt einer Normalverteilung mit einem Mittelwert von 1,62 m und einer Standardabweichung von 0,12 m. Wie groß ist die Wahrscheinlichkeit, dass der Mittelwert einer Zufallsstichprobe von 100 Schülerinnen größer als 1,60 m ist?
Diese Aufgabe wird in ähnlicher Weise gelöst wie die vorherige Aufgabe. Wir haben eine Zufallsvariable  , die einer Normalverteilung folgt. Das heißt:
, die einer Normalverteilung folgt. Das heißt:
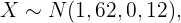
Somit folgt der Durchschnittswert ebenfalls einer Normalverteilung
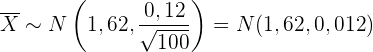
Die Wahrscheinlichkeit wird also wie folgt berechnet
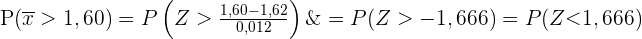
Wenn wir in diesem Fall eine Normalverteilungstabelle verwenden, ist das Ergebnis
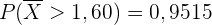
Wenn wir hingegen ein Computerprogramm verwenden, erhalten wir das folgende Ergebnis
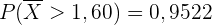
Auch hier gilt, dass das Ergebnis mit Computerprogrammen immer genauer ist. Unabhängig davon, welche Methode man anwendet, kommt das Ergebnis immer recht nahe an das reale Ergebnis heran (man beachte, dass die Ergebnisse auf zwei Stellen nach dem Komma gleich sind).
Salz wird maschinell in Säcke verpackt. Die Säcke haben ein Durchschnittsgewicht von  mit einer Standardabweichung von
mit einer Standardabweichung von 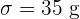 . Die Säcke wurden in Kartons zu jeweils 100 Stück verpackt.
. Die Säcke wurden in Kartons zu jeweils 100 Stück verpackt.
a Berechne die Wahrscheinlichkeit, dass der Durchschnitt der Gewichte der Säcke eines Kartons weniger als 495 g beträgt.
b Berechne die Wahrscheinlichkeit, dass ein Karton mit 100 Säcken mehr als 51 kg wiegt.
a Zur Beantwortung der ersten Frage müssen wir bedenken, dass der Durchschnittswert einer Stichprobe mit dem Umfang  einer Normalverteilung folgt (aufgrund des zentralen Grenzwertsatzes). Das heißt:
einer Normalverteilung folgt (aufgrund des zentralen Grenzwertsatzes). Das heißt:
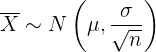
Die durchschnittliche Anzahl der Säcke in jedem Karton entspricht daher der folgenden Verteilung
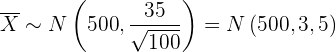
Um die Wahrscheinlichkeit zu berechnen, gehen wir wie folgt vor:
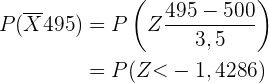 ,
,
wobei  eine Zufallsvariable mit Standardnormalverteilung ist.
eine Zufallsvariable mit Standardnormalverteilung ist.
Diese Wahrscheinlichkeit kann auf verschiedene Weise berechnet werden, zum Beispiel mit Excel oder einer Programmiersprache wie R.
Eine andere Möglichkeit, diese Wahrscheinlichkeit zu berechnen, ist die Verwendung einer Wahrscheinlichkeitstabelle der Normalverteilung, für die wir die Wahrscheinlichkeit wie folgt schreiben müssen:
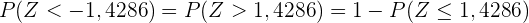
Wir können 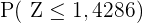 nun in einer Normalverteilungstabelle nachschlagen. Wir erhalten
nun in einer Normalverteilungstabelle nachschlagen. Wir erhalten 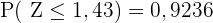 (dies ist der nächstliegende Wert, da er nur auf 2 Stellen genau ist). Somit
(dies ist der nächstliegende Wert, da er nur auf 2 Stellen genau ist). Somit
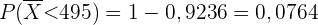
Bei Verwendung einer Programmiersprache ist das Ergebnis
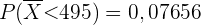 ,
,
was ziemlich ähnlich ist.
b Dieser Abschnitt ist ähnlich wie der vorherige. Der einzige Unterschied besteht darin, dass die Zufallsvariable jetzt die Summe der 100 Elemente der Stichprobe ist. In diesem Fall ergibt sich nach dem zentralen Grenzwertsatz
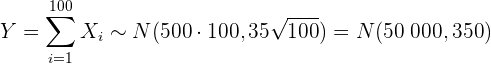 ,
,
wobei  das Gewicht des Kartons in Gramm ist. Somit ist die gesuchte Wahrscheinlichkeit
das Gewicht des Kartons in Gramm ist. Somit ist die gesuchte Wahrscheinlichkeit 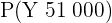 , da 51 kg 51 000 g sind.
, da 51 kg 51 000 g sind.
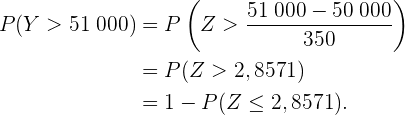
Wenn wir also eine Normalverteilungstabelle verwenden, ist das Ergebnis
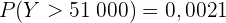 .
.
Wenn wir hingegen Excel oder eine Programmiersprache verwenden, lautet das Ergebnis
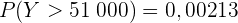
Beachte, dass das mit einem Computer erzielte Ergebnis genauer ist.
Hypothesentests mit Teststatistik
In einer Fabrik für elektronische Bauteile betrug der Anteil der fehlerhaften Endbauteile 20 %. Nach einer Reihe von Maßnahmen und Investitionen zur Verbesserung der Leistung wurde eine Zufallsstichprobe von 500 Bauteilen analysiert, von denen sich 90 als fehlerhaft erwiesen. Welches Konfidenzniveau sollte zugrunde gelegt werden, um anzunehmen, dass die Leistung unverändert geblieben ist?
Um das Konfidenzniveau zu bestimmen, müssen wir zunächst feststellen, dass es sich um einen Hypothesentest handelt, bei dem Anteile verglichen werden sollen.
Somit lautet die Nullhypothese (wobei 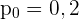 )
)
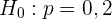
Die Alternativhypothese ist
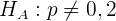
Bei der Stichprobe ergab sich, dass  ,
,  und
und
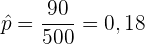
In diesem Fall ist die Teststatistik
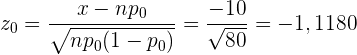 ,
,
wobei 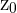 einer Standardnormalverteilung folgt. Um die Nullhypothese zu akzeptieren (d. h. anzunehmen, dass es keine Schwankungen bei der Leistung gibt), genügt es also, dass
einer Standardnormalverteilung folgt. Um die Nullhypothese zu akzeptieren (d. h. anzunehmen, dass es keine Schwankungen bei der Leistung gibt), genügt es also, dass  , wobei
, wobei  das Konfidenzniveau ist.
das Konfidenzniveau ist.
Es genügt also, 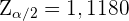 zu nehmen, um die Nullhypothese zu akzeptieren. Und somit
zu nehmen, um die Nullhypothese zu akzeptieren. Und somit
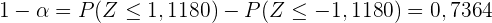
Das bedeutet, dass ein Konfidenzniveau von nur 73,64 % bereits ausreicht, um anzunehmen, dass die Leistung unverändert ist. Das Konfidenzniveau kann jedoch auch bei 80 % oder sogar 99 % liegen.
Wenn wir die Nullhypothese akzeptieren, drücken wir einfach nur aus, dass es keine ausreichenden Beweise gibt, um sie zu verwerfen.
Hinweis: Eine andere Möglichkeit, die Hypothese zu überprüfen, besteht darin, ein Konfidenzintervall ausgehend von 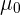 zu erstellen. Da die Hypothese zweiseitig ist, wird das Konfidenzintervall wie folgt berechnet
zu erstellen. Da die Hypothese zweiseitig ist, wird das Konfidenzintervall wie folgt berechnet
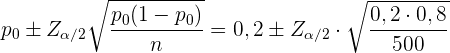
Das Konfidenzintervall ist
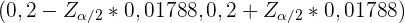
Für die Annahme der Hypothese genügt es, dass
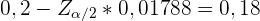
Wenn wir  bestimmen, erhalten wir
bestimmen, erhalten wir
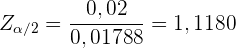 ,
,
was genau das war, was wir zuvor erhalten hatten. Daraus folgt, dass die Konfidenz bei 73,64 % liegt.
Ein Soziologe hat vorausgesagt, dass in einer bestimmten Stadt die Wahlenthaltung bei den nächsten Wahlen bei mindestens 40 % liegen wird. Es wird eine Zufallsstichprobe von 200 wahlberechtigten Personen ausgewählt, von denen 75 bereit wären zu wählen. Bestimme mit einem Signifikanzniveau von 1 %, ob die Vorhersage akzeptiert werden kann.
In diesem Fall handelt es sich um einen Hypothesentest für den Anteil. Allerdings handelt es sich jetzt um einen einseitigen Test, denn die Nullhypothese lautet
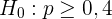
Die Alternativhypothese lautet
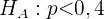 ,
,
wobei  der Anteil der Personen ist, die bei den nächsten Wahlen nicht wählen werden.
der Anteil der Personen ist, die bei den nächsten Wahlen nicht wählen werden. 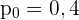 ist der hypothetische Anteil.
ist der hypothetische Anteil.
Die Teststatistik ist also
 ,
,
wobei 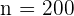 ,
, 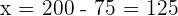 . Damit nimmt die Statistik den Wert von
. Damit nimmt die Statistik den Wert von
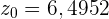 an.
an.
Da es sich um einen einseitigen Test handelt, wird die Hypothese abgelehnt, wenn 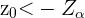 . Daher entspricht
. Daher entspricht 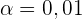 dem kritischen Wert
dem kritischen Wert 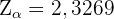 . Und da
. Und da
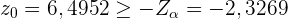 ,
,
akzeptieren wir  .
.
Daher kann man mit einem Signifikanzniveau von 1 % davon ausgehen, dass die Wahlenthaltung mindestens 40 % betragen wird.
Hinweis: Wenn wir ein Konfidenzintervall um 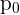 (einseitig) bilden, wäre die Untergrenze
(einseitig) bilden, wäre die Untergrenze

Wir setzen ein und erhalten
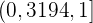
und da 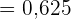 im Konfidenzintervall liegt, akzeptieren wir die Nullhypothese. Dies ist eine andere Form des Hypothesentests.
im Konfidenzintervall liegt, akzeptieren wir die Nullhypothese. Dies ist eine andere Form des Hypothesentests.
Aus einem Bericht geht hervor, dass der durchschnittliche Flugpreis zwischen den Kanarischen Inseln und Madrid höchstens 120 € beträgt, mit einer Standardabweichung von 40 €. Bei einer Stichprobe von 100 Reisenden liegt der Durchschnittspreis ihrer Tickets bei 128 €.
Kann die ursprüngliche Aussage bei einem Signifikanzniveau von 0,1 akzeptiert werden?
Bei diesem Hypothesentest wird geprüft, ob der Mittelwert kleiner oder gleich einem bestimmten Wert ist. Daher lautet die Nullhypothese
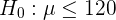
und die Alternativhypothese ist
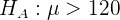 ,
,
wobei 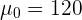 der hypothetische Wert ist. Durch die Stichprobe ergibt sich, dass
der hypothetische Wert ist. Durch die Stichprobe ergibt sich, dass  ,
, 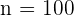 und
und 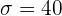 . Unsere Teststatistik ist also
. Unsere Teststatistik ist also
 ,
,
die den Wert 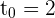 annimmt.
annimmt.
Da es sich um einen einseitigen Test handelt, ist das Kriterium für die Ablehnung der Nullhypthese  . In diesem Fall entspricht
. In diesem Fall entspricht 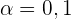 einem kritischen Wert von
einem kritischen Wert von 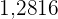 .
.
Und da
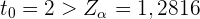 ,
,
verwerfen wir somit die Nullhypothese.
Daraus schließen wir, dass die durchschnittlichen Flugpreise nicht bei höchstens 120 € liegen. Wir haben Beweise, die bestätigen, dass der Durchschnitt höher als 120 € ist.
Ein Agrarwissenschaftler berichtet, dass der durchschnittliche Ertrag von Tomatenpflanzen mindestens 5 kg beträgt, mit einer Standardabweichung von 1,3 kg. Es wird eine Stichprobe von 90 Pflanzen genommen und der mittlere Ertrag pro Pflanze beträgt 4,5 kg.
Kann die ursprüngliche Aussage bei einem Signifikanzniveau von 0,1 akzeptiert werden?
Bei diesem Hypothesentest wird geprüft, ob der Mittelwert größer oder gleich einem bestimmten Wert ist. Daher lautet die Nullhypothese
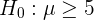
und die Alternativhypothese ist
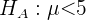 ,
,
wobei 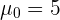 der hypothetische Wert ist. Bei Durchführung der Stichprobe erhalten wir
der hypothetische Wert ist. Bei Durchführung der Stichprobe erhalten wir 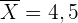 ,
, 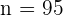 und
und 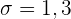 . Unsere Teststatistik ist also
. Unsere Teststatistik ist also
 ,
,
die den Wert 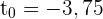 annimmt.
annimmt.
Da es sich um einen einseitigen Test handelt, ist das Kriterium für die Ablehnung der Nullhypothese 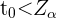 . In diesem Fall entspricht
. In diesem Fall entspricht 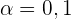 einem kritischen Wert von
einem kritischen Wert von 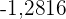 .
.
Und da
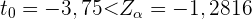 ,
,
verwerfen wir somit die Nullhypothese.
Daraus schließen wir, dass der durchschnittliche Ertrag der Tomatenpflanzen nicht bei mindestens 5 kg liegt. Wir haben Beweise, die bestätigen, dass der Durchschnitt weniger als 5 kg beträgt.
Hypothesentests mit Konfidenzintervallen
Ein Lampenhersteller testet ein neues Produktionsverfahren, das als akzeptabel gilt, wenn die nach diesem Verfahren hergestellten Lampen eine durchschnittlichen Lebensdauer von 2400 Stunden haben und die Standardabweichung 300 beträgt. Es wird eine Stichprobe von 100 nach diesem Verfahren hergestellten Lampen entnommen, die eine durchschnittliche Lebensdauer von 2320 Stunden hat. Kann die Hypothese der Eignung des neuen Produktionsverfahrens mit einem Risiko von 5 % oder weniger akzeptiert werden?
In diesem Fall handelt es sich um einen Hypothesentest, bei dem überprüft werden soll, ob der Mittelwert gleich einem bestimmten Wert ist. Daher lautet die Nullhypothese
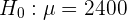
und die Alternativhypothese ist
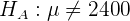 ,
,
wobei 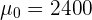 der hypothetische Wert ist.
der hypothetische Wert ist.
Da wir den Mittelwert der Grundgesamtheit testen, wird das Konfidenzintervall wie folgt gebildet
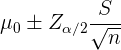 ,
,
da es sich um einen zweiseitigen Test handelt. Wir erhalten aus der Stichprobe 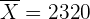 ,
, 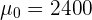 ,
,  und
und 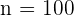 . Der Signifikanz
. Der Signifikanz 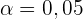 entspricht ein kritischer Wert von
entspricht ein kritischer Wert von 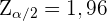 . Das Konfidenzintervall ist also
. Das Konfidenzintervall ist also
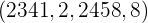
und da 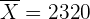 außerhalb des Konfidenzintervalls liegt, verwerfen wir die Nullhypothese.
außerhalb des Konfidenzintervalls liegt, verwerfen wir die Nullhypothese.
Wir kommen daher zu dem Schluss, dass das neue Herstellungsverfahren nicht akzeptabel ist.
Die Qualitätskontrolle einer Akkufabrik vermutet, dass bei der Produktion eines Akkumodells für Mobiltelefone Fehler aufgetreten sind, die die Lebensdauer des Akkus verringern. Bislang folgte die Gesprächszeit einer Normalverteilung mit einem Mittelwert von 300 Minuten und einer Standardabweichung von 30 Minuten. Bei der Überprüfung der letzten produzierten Charge vor der Auslieferung an den Handel wurde jedoch festgestellt, dass bei einer Stichprobe von 60 Akkus die durchschnittliche Gesprächszeit 290 Minuten betrug. Angenommen, diese Zeit bleibt normal mit der gleichen Standardabweichung:
Kann man bei einem Signifikanzniveau von 2 % davon ausgehen, dass der Verdacht der Qualitätskontrolle zutrifft?
Da wir davon ausgehen, dass die Lebensdauer verkürzt wurde, handelt es sich um einen Hypothesentest, bei dem wir überprüfen wollen, ob der Mittelwert unter einem bestimmten Wert liegt. Die Nullhypothese lautet also
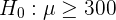
und die Alternativhypothese ist
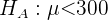 ,
,
wobei  der hypothetische Mittelwert ist.
der hypothetische Mittelwert ist.
Das Konfidenzintervall für den Mittelwert ist
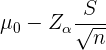
Für diese Stichprobe haben wir  ,
,  ,
,  und
und  . Da es sich um einen einseitigen Test handelt, betrachten wir nur die untere Grenze (da die obere Grenze
. Da es sich um einen einseitigen Test handelt, betrachten wir nur die untere Grenze (da die obere Grenze  wäre). Bei einer Signifikanz von
wäre). Bei einer Signifikanz von 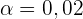 ist der zugehörige kritische Wert
ist der zugehörige kritische Wert 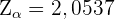 . Das Konfidenzintervall ist also
. Das Konfidenzintervall ist also
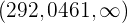
Und da  nicht im Konfidenzintervall liegt, ist das Kriterium der Ablehnung erfüllt.
nicht im Konfidenzintervall liegt, ist das Kriterium der Ablehnung erfüllt.
Folglich verwerfen wir die Nullhypothese. Daher akzeptieren wir den Verdacht der Qualitätskontrolle, dass die Lebensdauer der Akkus weniger als 300 Minuten beträgt (mit einer Konfidenz von 2 %).
Man geht davon aus, dass der mittlere Protombin-Spiegel in einer normalen Grundgesamtheit 20 mg/100 ml Plasma mit einer Standardabweichung von 4 Milligramm/100 ml beträgt. Um dies zu prüfen, wird eine Stichprobe von 40 Personen genommen, bei denen der Mittelwert 18,5 mg/100 ml beträgt. Kann die Hypothese mit einem Signifikanzniveau von 5 % akzeptiert werden?
In diesem Fall handelt es sich um einen Hypothesentest, bei dem überprüft werden soll, ob der Mittelwert gleich einem bestimmten Wert ist. Die Nullhypothese lautet also
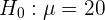
Die Alternativhypothese ist
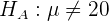 ,
,
wobei 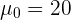 der kritische Wert ist
der kritische Wert ist
Da wir einen Test für den Mittelwert durchführen und es sich um einen zweiseitigen Test handelt, wird das Konfidenzintervall wie folgt berechnet
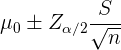 ,
,
wobei 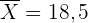 ,
, 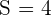 ,
,  und
und 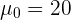 . Für eine Signifikanz von
. Für eine Signifikanz von 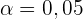 haben wir
haben wir 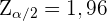 . Das Konfidenzintervall ist also
. Das Konfidenzintervall ist also
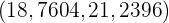
Und da 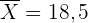 nicht im Konfidenzintervall liegt, verwerfen wir die Nullhypothese.
nicht im Konfidenzintervall liegt, verwerfen wir die Nullhypothese.
Daraus schließen wir, dass der mittlere Protombin-Spiegel nicht 20 mg / 100 ml Plasma beträgt.
Ein Apfelerzeuger verkauft seine Ernte in Kisten zu 25 kg mit einer Standardabweichung von 1 kg. Um dies zu überprüfen, wird eine Stichprobe von 30 Kisten genommen, deren Mittelwert 24,5 kg beträgt. Kann die Hypothese mit einem Signifikanzniveau von 2 % akzeptiert werden?
In diesem Fall handelt es sich um einen Hypothesentest, bei dem überprüft werden soll, ob der Mittelwert gleich einem bestimmten Wert ist. Die Nullhypothese lautet also
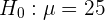 ,
,
während die Alternativhypothese wie folgt lautet
 ,
,
wobei  der hypothetische Wert ist
der hypothetische Wert ist
Da wir einen Test für den Mittelwert durchführen und es sich um einen zweiseitigen Test handelt, wird das Konfidenzintervall wie folgt berechnet
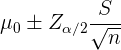 ,
,
wobei 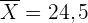 ,
, 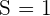 ,
, 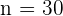 und
und  . Für eine Signifikanz von
. Für eine Signifikanz von 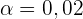 haben wir
haben wir 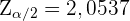 . Daher ist das Konfidenzintervall
. Daher ist das Konfidenzintervall
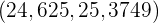
Und da 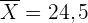 nicht im Konfidenzintervall liegt, verwerfen wir die Nullhypothese.
nicht im Konfidenzintervall liegt, verwerfen wir die Nullhypothese.
Daraus schließen wir, dass das Durchschnittsgewicht jeder Kiste Äpfel nicht 25 kg beträgt.
Mit KI zusammenfassen:












