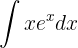
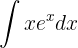
Wir lösen durch partielle Integration
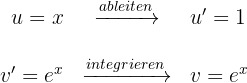
Wir setzen in die Formel der partiellen Integration ein
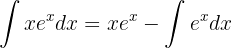
Wir lösen das neue Integral
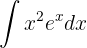
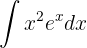
Wir lösen durch partielle Integration
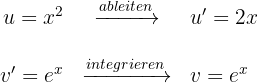
Wir setzen in die Formel der partiellen Integration ein
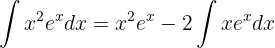
Wir lösen das zweite Integral, das wir durch die partielle Integration erhalten
Wir setzen in die Formel der partiellen Integration ein
Wir lösen das neue Integral
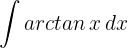
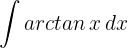
Wir lösen durch partielle Integration
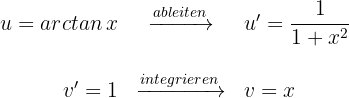
Wir setzen in die Formel der partiellen Integration ein
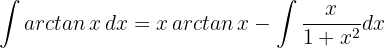
Wir lösen das neue Integral
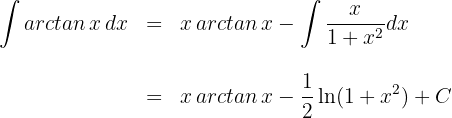
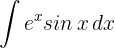
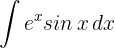
Wir lösen durch partielle Integration
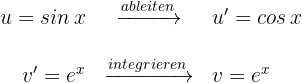
Wir setzen in die Formel der partiellen Integration ein
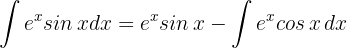
Wir lösen das zweite Integral, das wir durch die partielle Integration erhalten
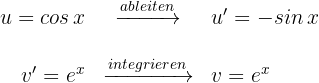
Wir setzen in die Formel der partiellen Integration ein
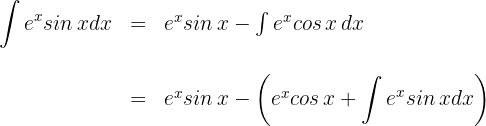
Wir lösen das neue Integral
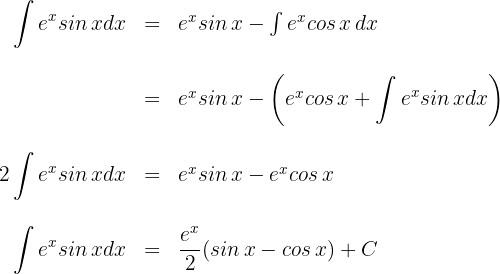
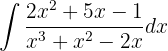
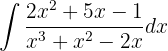
Wir lösen durch Partialbruchzerlegung
Wir addieren:
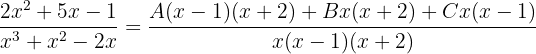
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
Wir berechnen die Koeffizienten von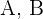 
und 
. 
weisen wir die Werte zu, für die der Nenner 0 wird.
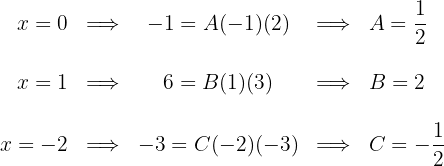
Wir berechnen die Integrale der Brüche:
Eine andere Möglichkeit, die Koeffizienten zu ermitteln, besteht darin, die entsprechenden Rechenoperationen durchzuführen und die Koeffizienten gleichzusetzen.
Wir setzen die Koeffizienten gleich:
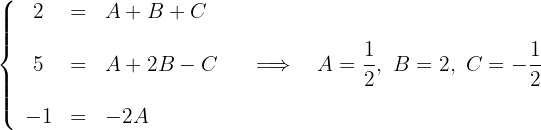
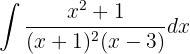
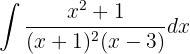
Wir lösen durch Partialbruchzerlegung
Wir addieren:
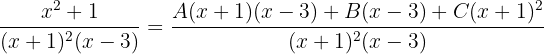
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
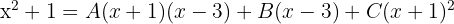
Um die Wert von 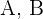und zu berechnen, weisen wir die Werte zu, für die der Nenner 0 wird sowie einen weiteren
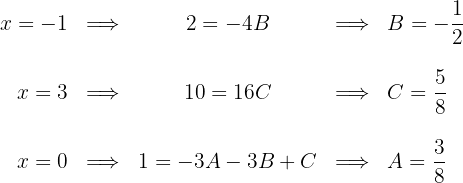
Wir berechnen die Integrale der Brüche:
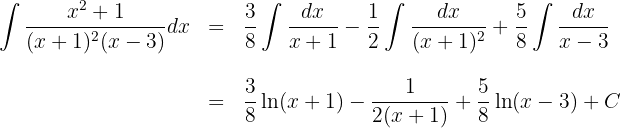
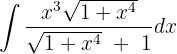
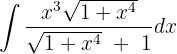
Wir substituieren
Wir berechnen das Differential auf beiden Seiten
Wir setzen in das Integral ein und lösen nach 
Wir substituieren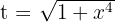 
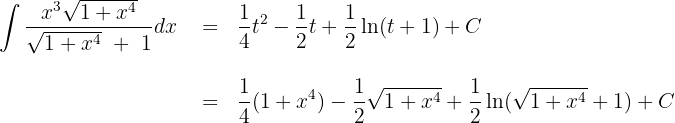
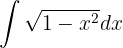
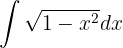
Wir substituieren
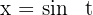
Wir berechnen das Differential auf beiden Seiten
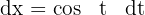
Wir setzen in das Integral ein und lösen nach
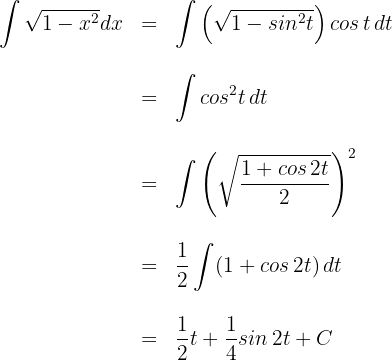
Wir substituier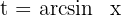en 
en
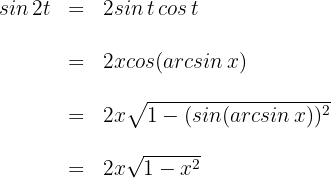
Wir substituieren den vorherigen Ausdruch und erhalten die Lösung
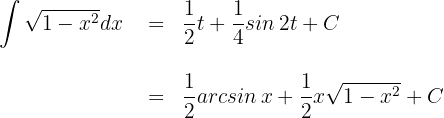
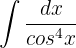
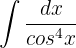
Wir substituieren
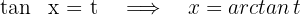
Wir berechnen das Differential auf beiden Seiten
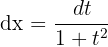
Wir setzen den Ausdruck des Differentials und der Äquivalenz in das Integral ein: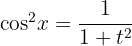 
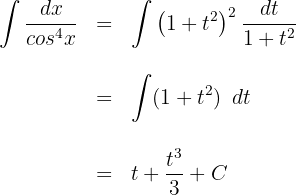
Wir substituieren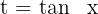 
in der Lösung
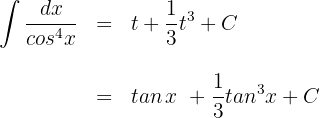
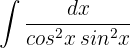
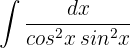
Wir substituieren
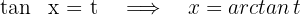
Wir berechnen das Differential auf beiden Seiten
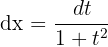
Wir setzen den Ausdruck des Differentials und der Äquivalenzen in das Integral ein: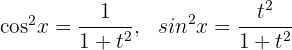 
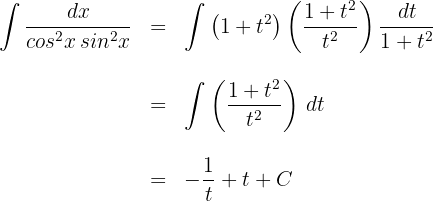
Wir substituieren 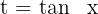in der Lösung
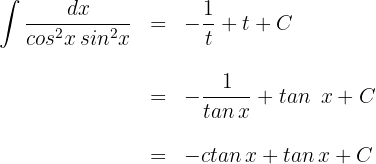
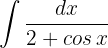
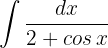
Wir substituieren
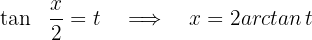
Wir berechnen das Integral auf beiden Seiten
Wir setzen den Ausdruck des Differentials und der Äquivalenz in das Integral ein: 
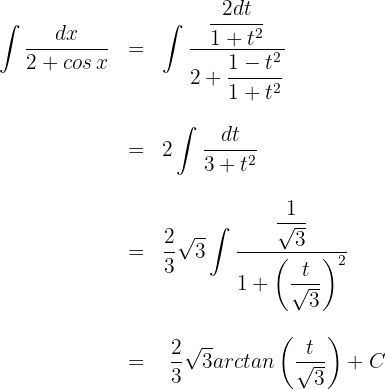
Wir substituieren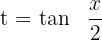 
in der Lösung
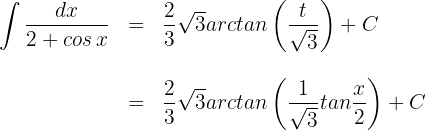
Wir substituieren
Wir berechnen das Integral auf beiden Seiten
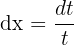
Wir setzen den Ausdruck des Differentials in das Integral ein:
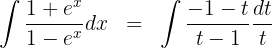
Wir lösen durch Partialbruchzerlegung
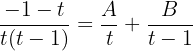
Wir addieren:
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
Um die Werte von 
y 
zu berechnen, weisen wir die Werte zu, für die der Nenner 0 wird
Wir berechnen die Integrale der Brüche:
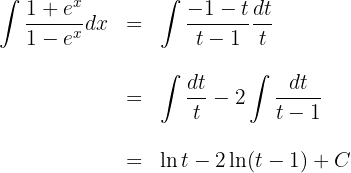
Wir substituieren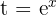 
in der Lösung
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
