Was bedeutet das bestimmte Integral und wie kann man es berechnen?
Der Fundamentalsatz der Analysis (oder Hauptsatz der Differential- und Integralrechnung) besagt, dass das bestimmte Integral wie folgt berechnet werden kann
,
wobei 
eine beliebige Stammfunktion von 
ist.
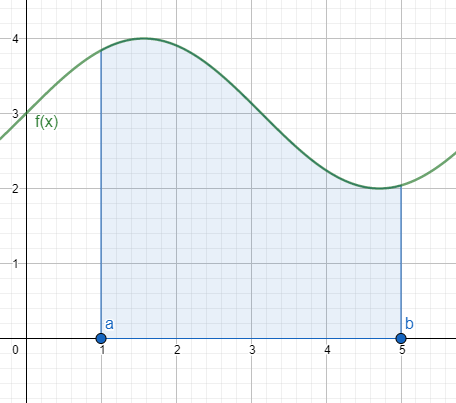
Wir denken außerdem daran, dass das bestimmte Integral die Fläche unter dem Graphen von zwischen den Punkten 
und 
misst, wie in der folgenden Abbildung dargestellt:
Aufgaben mit Lösungen
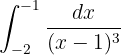
Das erste Integral kann mit der Formel für die Integration einer Potenz gelöst werden. Wir gehen wie folgt vor
Wir können die Formel anwenden
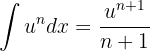
und substituieren: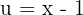 
und 
(beachte, dass bei bestimmten Integralen die Integrationskonstante nicht notwendig ist). So erhalten wir
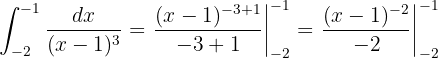
Das heißt:
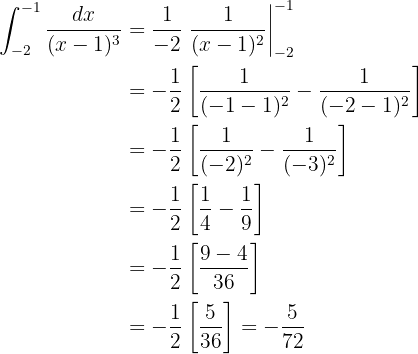
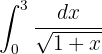
Wie im vorherigen Fall wird dieses Integral mit der Formel für die Integration einer Potenz gelöst:
wir vereinfachen ein wenig
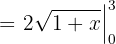
Wir untersuchen an den Grenzen des Integrals:
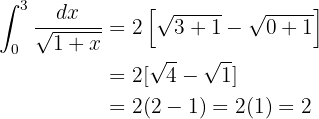
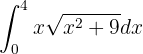
Dieses Integral wird mit der Substitution gelöst. Wir sehen, dass unter der Wurzel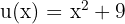 
steht. Wenn wir ableiten, haben wir 
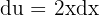; wir lösen nach 
und erhalten
Da wir die Substitution anwenden, müssen wir auch die Grenzen des Integrals ändern. Insbesondere
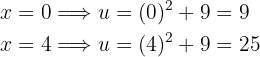
Das Integral wird also zu
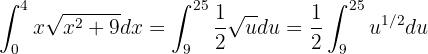
Wir lösen nun das Integral mithilfe der Formel für das Integral einer Potenz:
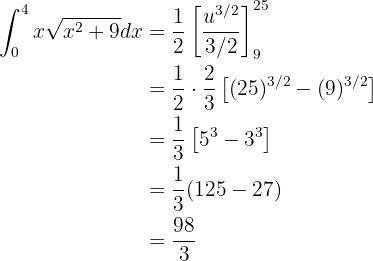
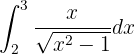
Wie im vorherigen Fall substituieren wir wie folgt
Wenn wir ableiten, erhalten wir 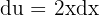. Wir lösen nach (denn das ist es, was wir innerhalb des Integranden haben) und erhalten
Wir erhalten nun die neuen Grenzen:
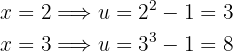
Das Integral wird also zu
Wir integrieren mit der Formel des Integrals einer Potenz:
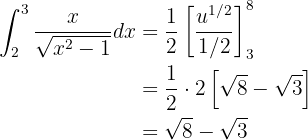
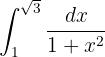
Dieses Integral kann sehr schnell gelöst werden, wenn wir bedenken, dass
Das Integral kann also sofort gelöst werden:
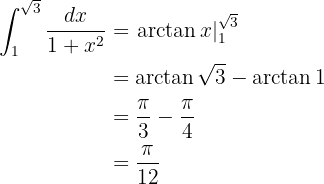
Beachte, dass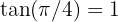 
und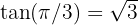 
(das Merken dieser Werte ist nützlich, wenn wir die Werte des Arkustangens ermitteln möchten).
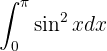
Um dieses Integral zu lösen, benötigen wir eine trigonometrische Identität. Da wir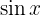 
auf eine gerade Potenz (in diesem Fall 2) erhöht haben, benötigen wir eine Potenz, die sich auf eine ungerade Potenz verringert. Dies ergibt sich aus der Identität des doppelten Winkels für den Kosinus:
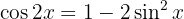
Wenn wir nach 
auflösen, erhalten wir
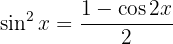
Das Integral wird also zu
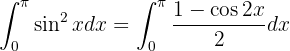
Dies kann nun auf einfachere Art und Weise integriert werden:
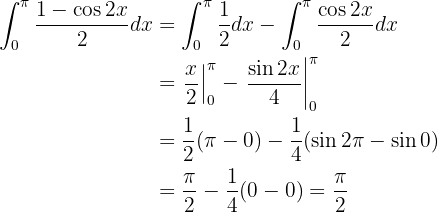
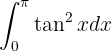
Es ist etwas schwierig, durch Ausprobieren eine Funktion zu finden, bei der 
). Aus diesem Grund ist es besser,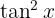 
mithilfe einer pythagoräischen Identität zu umzuformen. Das heißt
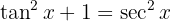
Somit ist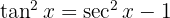 
. Das Integral wird also zu
Da
,
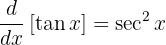können wir das Integral also sofort lösen:
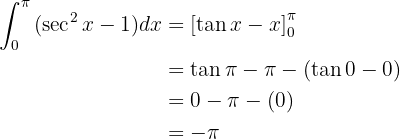
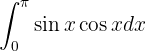
Für dieses Integral brauchen wir keine trigonometrische Identität zu verwenden, da weder 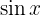noch 
potenziert sind. Wir nehmen also
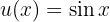
Und somit
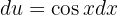
Beachte, dass die Substitution nicht bijektiv (eins-zu-eins) im Definitionsbereich ist. Daher ist es notwendig, vor der Auswertung zur ursprünglichen Variable zurückzukehren:
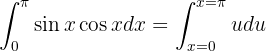
Wir berechnen die Stammfunktion:
Wir kehren zur vorherigen Variable zurück:
Nun untersuchen wir an den Grenzen des Integrals:
Dies ist unser gesuchtes Ergebnis.
Hinweis: Wenn wir 
genommen hätten, hätten wir das Integral ganz einfach berechnen können.
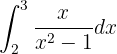
Beachte, dass wir in diesem Integral auch eine Änderung der Variablen haben. Somit
,
woraus folgt, dass 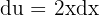ist. Somit
Außerdem
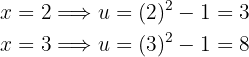
Das Integral wird also zu
Wir lösen, werten aus und erhalten
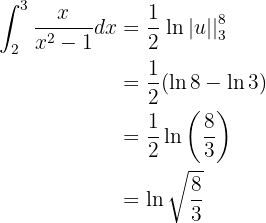
Auch wenn es nicht sofort ersichtlich ist, kann dieses Integral ebenfalls mit der Substitution gelöst werden (beachte, dass nicht alle Integrale mit der Substitution gelöst werden können). Wir nehmen
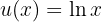
Und somit
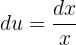
Die Grenzen werden zu
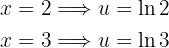
Das Integral wird also zu
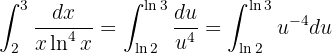
Wenn wir also das Integral lösen und an den Grenzen auswerten, erhalten wir
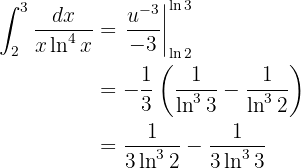
Weiter können wir nicht vereinfachen.
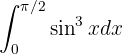
Bei diesem Integral haben wir eine ungerade Potenz von 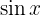. Wir müssen eine Substitution durchführen, bei der 
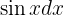ein Teil des Differentials der neuen Variablen sein wird. Wir unterteilen also wie folgt:
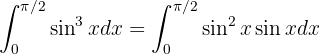
Nun wenden wir den Satz des Pythagoras an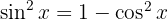 
und erhalten so
Wir können substituieren: , weshalb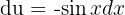 
ist. Somit
Außerdem ist die Substitution im Integrationsintervall injektiv, daher:
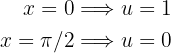
Das Integral wird also zu
Wir lösen das Integral und erhalten
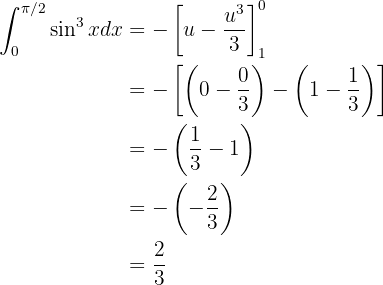
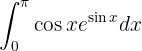
Hier können wir sofort sehen, dass wir eine Änderung der Variablen haben. Wir nehmen
,
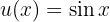weshalb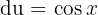 
. Das Integral wird also zu
Wir integrieren und erhalten
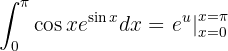
Wir kehren zur vorherigen Variablen zurück und werten an den Grenzen aus:
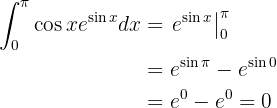
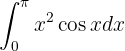
Dieses Integral wird durch partielle Integration gelöst. Zuerst lösen wir das Integral, ohne uns um die Grenzwerte zu kümmern, und dann werten wir aus:
Da wir ein Polynom multipliziert mit haben, nehmen wir 
und 
. Somit
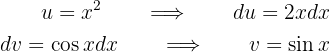
Das Integral ist nun
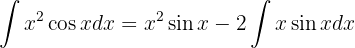
Wir wiederholen den Vorgang erneut, diesmal mit
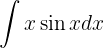
Wir nehmen 
und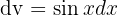 
. Hier haben wir:
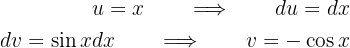
daher wird dieses zweite Integral zu
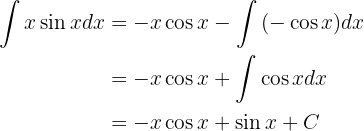
Wir setzen in das ursprüngliche Integral ein und erhalten
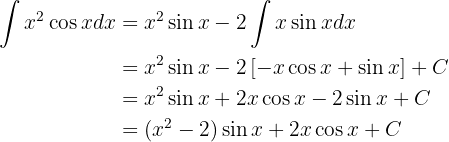
Da wir nun das unbestimmte Integral haben, werten wir an den Integrationsgrenzen aus:
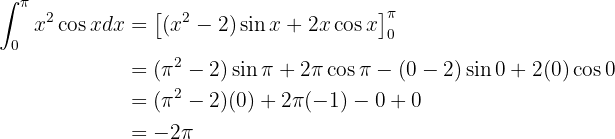
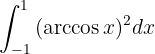
Das Lösen von Integralen mit trigonometrischen Funktionen ist etwas komplizierter. Normalerweise versuchen wir, irgendeine Art von Substitution anzuwenden, wie z.B.
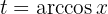
(obwohl das nicht immer funktioniert). Wenn wir nach 
auflösen, erhalten wir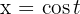 
. Somit
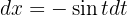
Daraus folgt, dass
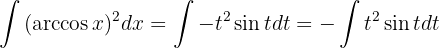
Dieses Integral wird ebenfalls partiell gelöst. Wir nehmen zunächst 
und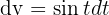 
, weshalb
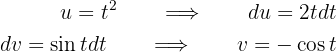
Das Integral wird zu
Nun nehmen wir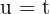 
und 
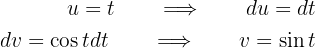
Somit ist das Integral
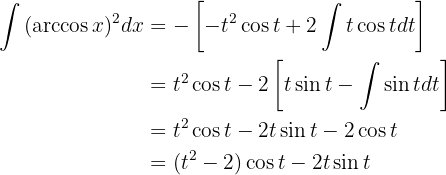
Wir können zur inneren Variablen zurückkehren oder die Grenzen des Integrals ändern. Wir entscheiden uns für die 2. Option:
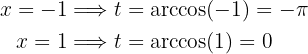
Das Integral ist somit
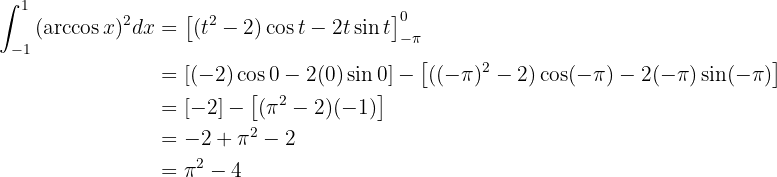
Schließlich lösen wir dieses Integral mit Substitution, um die Wurzel loszuwerden. Wir nehmen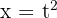 
und erhalten
,
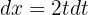wobei wir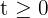 
haben. Somit ist 
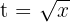und
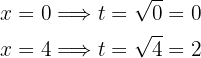
Das Integral wird zu
Wir müssen den Integranden ein wenig umformen. Somit
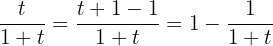
Wir erhalten
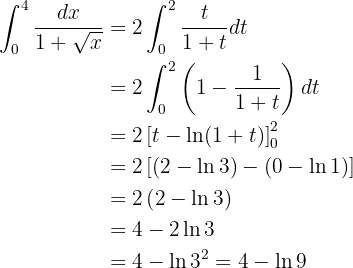
Dies ist das Ergebnis des Integrals.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
