Kapitel
Das bestimmte Integral ist ein Fall des Integrals, das verwendet wird, um den Wert der Flächen zu bestimmen, die von einem Graphen innerhalb eines Intervalls und der horizontalen Achse begrenzt werden. Es kommt in verschiedenen Bereichen und Kontexten vor, z. B. in der Biologie (Populationswachstum), in der Robotik, in der Architektur (Volumina von Festkörpern) usw. Ein konkretes Beispiel für eine Anwendung wird später gegeben.
Formal ist es wie folgt definiert:
Definition des bestimmten Integrals
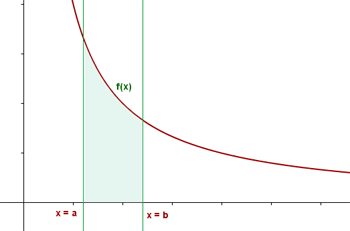
Gegeben ist eine Funktion f(x) mit einer reellen Variable x und einem Intervall [a,b] der Zahlengerade. Das bestimmte Integral ist gleich der Fläche, die durch den Graphen von f(x), die x-Achse und die senkrechten Geraden x = a und x = b begrenzt wird.
Es wird mit 
dargestellt.
ist das Integralzeichen.- a ist die untere Grenze der Integration.
- b ist die obere Grenze der Integration.
ist der Integrand oder die zu integrierende Funktion.
ist das Differential von x und gibt an, welche Variable der Funktion integriert wird.
Eigenschaften des bestimmten Integrals
1 Der Wert des bestimmten Integrals wechselt das Vorzeichen, wenn die Grenzen der Integration vertauscht werden.
Diese Eigenschaft kann uns helfen, dass wir nicht mit negativen Vorzeichen rechnen müssen.
Beispiel:
2 Wenn die Integrationsgrenzen übereinstimmen, ist das bestimmte Integral gleich null.
Da die Integrationsgrenze an beiden Seiten dieselbe ist, gibt es keine zu berechnende Fläche, weshalb das Integral in diesem Fall 0 ist.
Beispiel:
3 Wenn c ein innerer Punkt des Intervalls [a, b] ist, kann das bestimmte Integral in eine Summe von zwei Integralen zerlegt werden, die sich auf die Intervalle [a, c] und [c, b] erstrecken.
Da der Punkt c zwischen a und b auf der x-Achse liegt, ist die durch das Intervall [a,b] begrenzte Fläche die Summe der durch [a,c] und [c,d] begrenzten Flächen; dasselbe gilt für den Wert des Integrals.
Beispiel:
Die Zahl 7 soll zum Intervall [3,10] gehören:
4 Das bestimmte Integral einer Summe von Funktionen ist gleich der Summe der Integrale.
Diese Eigenschaft kann uns helfen, sehr lange Ausdrücke innerhalb desselben Integrals zu vermeiden und so die Handhabung und die Berechnungen zu vereinfachen, oder im anderen Fall Ausdrücke zu gruppieren, um eine einfachere Berechnung zu ermöglichen.
Beispiel:
Für 
und 
,
5 Das Integral des Produkts aus einer Konstanten k und einer Funktion ist gleich der Konstanten k multipliziert mit dem Integral der Funktion.
Dies bedeutet, dass die Konstante aus dem Integral herausgenommen wird.
Beispiel:
Für die Konstante k=3
Beispiel der Anwendung
In diesem Beispiel setzen wir die oben genannten Eigenschaften zur besseren Veranschaulichung in eine Anwendung des Integrals beim Bevölkerungswachstum um.
Eine Bevölkerung wächst mit einer Rate von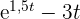 
Personen pro Jahr (wobei 
die Anzahl der Jahre ist). Im ersten Jahr liegt die Bevölkerung bei 1500 Personen.
Um wie viel ist die Bevölkerung zwischen dem ersten und dem dritten Jahr gewachsen und wie hoch ist die Bevölkerung im dritten Jahr?
1 Da die Frage nach dem Bevölkerungswachstum zwischen 1 und 3 gestellt wird, d. h. nach der Fläche unter der Kurve der Wachstumsrate zwischen 1 und 3, wird sie wie folgt ausgedrückt:
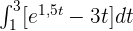
Anmerkung: Die folgenden Schritte dienen der Veranschaulichung, einige davon können weggelassen werden.
2 Bei den Berechnungen ist zu beachten, dass wir die Eigenschaft 4 verwenden und eine Summe bilden können.
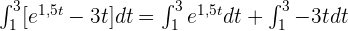
3 Wir können auch Eigenschaft 5 verwenden und die Konstante -3 herausnehmen, die mit t multipliziert wird.
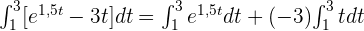
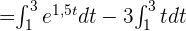
4 Da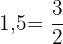 
, setzen wir ein und führen die entsprechenden Berechnungen durch, damit wir die 1. Frage beantworten können:
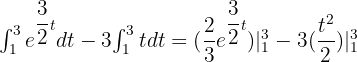
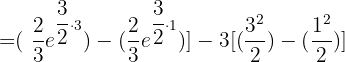
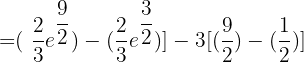
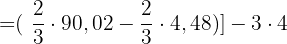
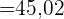
Somit betrug der Zuwachs zwischen dem ersten und dritten Jahr etwa 33 Personen.
6 Bei der zweiten Frage gehen wir von folgender Überlegung aus:
- Im Jahr 1 betrug die Bevölkerung 1000 Personen.
- Der Zuwachs zwischen dem 1. und 3. Jahr betrug etwa 33 Personen.
- Somit beträgt die Bevölkerung im Jahr 3 etwa 1033 Personen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
