Kapitel

Übungsaufgaben
Bestimme die Fläche, die durch die Gerade  , die
, die  -Achse sowie die Geraden
-Achse sowie die Geraden  und
und 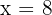 definiert ist.
definiert ist.
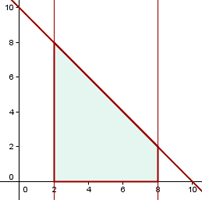
1 Wir stellen die Geraden sowie die angegebenen Achsen grafisch dar und zeichnen die gesuchte Fläche ein
2 Die Extremwerte der gesuchten Fläche sind durch die Geraden  und
und 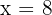 gegeben. Wir stellen die Gerade also in Funktion der Variable
gegeben. Wir stellen die Gerade also in Funktion der Variable  dar
dar
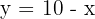
3 Die gesuchte Fläche ist gegeben durch

4 Wir setzen  in die Funktion von
in die Funktion von  ein und lösen das bestimmte Integral
ein und lösen das bestimmte Integral

Berechne die durch den Graphen 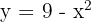 und die
und die  -Achse begrenzte Fläche.
-Achse begrenzte Fläche.
1 Wir bestimmen die Punkte, an denen der Graph die  -Achse schneidet, da diese die Integrationsgrenzen sind; hierfür setzen wir den Graphen gleich null und bestimmen die Werte für
-Achse schneidet, da diese die Integrationsgrenzen sind; hierfür setzen wir den Graphen gleich null und bestimmen die Werte für 
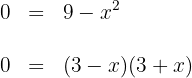
somit sind 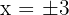 die Punkte, an denen der Graph die
die Punkte, an denen der Graph die  -Achse schneidet. Grafisch dargestellt:
-Achse schneidet. Grafisch dargestellt:
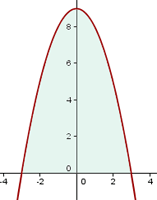
2 Die gesuchte Fläche ist gegeben durch
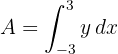
3 Wir setzen  in die Funktion von
in die Funktion von  ein und lösen das bestimmte Integral
ein und lösen das bestimmte Integral

Da die 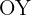 -Achse die Symmetrieachse der Parabel ist, ist die Fläche gleich dem Doppelten der Fläche zwischen
-Achse die Symmetrieachse der Parabel ist, ist die Fläche gleich dem Doppelten der Fläche zwischen  und
und 
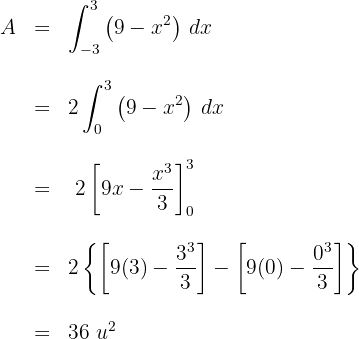
Berechne die Fläche des Dreicks mit den Eckpunkten 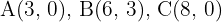 .
.
1 Wir stellen die gegebenen Punkte grafisch dar und zeichnen die gesuchte Fläche ein
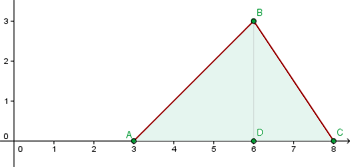
2 Wir berechnen die Steigungen der Geraden  und
und  und ermitteln die entsprechenden Gleichungen der Geraden
und ermitteln die entsprechenden Gleichungen der Geraden

3 Die gesuchte Fläche wird in zwei Teilen angegeben, einer für jede Gerade

4 Wir setzen die Geraden in Funktion von  ein und lösen das bestimmte Integral
ein und lösen das bestimmte Integral
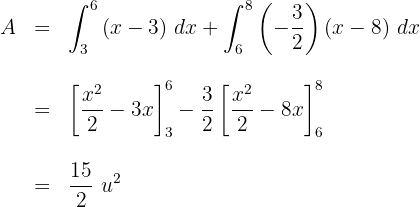
Berechne die durch die Graphen 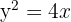 und
und  begrenzte Fläche.
begrenzte Fläche.
1 Wir stellen die Graphen grafisch dar und zeichnen die gesuchte Fläche ein
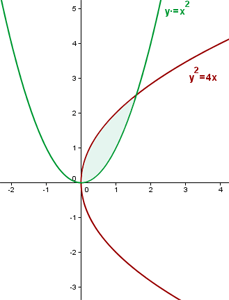
2 Wir berechnen die Integrationsgrenzen. Hierfür suchen wir die Punkte, an denen sich die Graphen schneiden
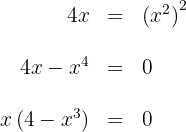
somit sind  und
und 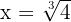 die Integrationsgrenzen.
die Integrationsgrenzen.
33 beiden Graphen.
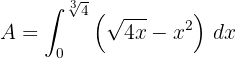
4 Wir lösen das bestimmte Integral

Berechne die Fläche, die durch den Graphen 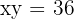 , die
, die  -Achse und die Geraden
-Achse und die Geraden  ,
,  begrenzt ist.
begrenzt ist.
1 Wir stellen die gegebenen Graphen grafisch dar und zeichnen die gesuchte Fläche ein
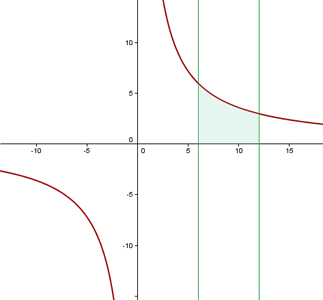
2 Die gesuchte Fläche ist gegeben durch
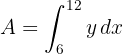
3 Wir setzen  in Funktion von
in Funktion von  ein und lösen das bestimmte Integral
ein und lösen das bestimmte Integral
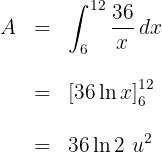
Berechne die Fläche, die durch den Graphen 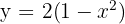 und die Gerade
und die Gerade 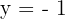 gegeben ist.
gegeben ist.
1 Wir stellen den Graphen und die gegebene Gerade grafisch dar. So können wir die gesuchte Fläche bestimmen.
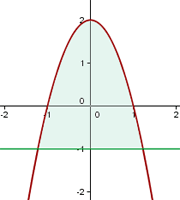
2 Wir berechnen die Integrationsgrenzen. Hierfür suchen wir die Punkte, an denen sich die Graphen schneiden
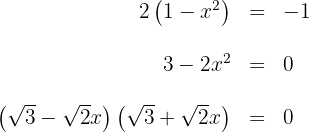
somit sind  die Integrationsgrenzen.
die Integrationsgrenzen.
3 Die gesuchte Fläche ergibt sich aus dem Integral der Differenz der beiden Graphen
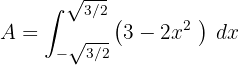
4 Wir lösen das bestimmte Integral und stellen fest, dass die 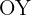 -Achse die Symmetrieachse der Fläche ist
-Achse die Symmetrieachse der Fläche ist

Berechne die Fläche, die durch die Parabel 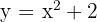 und die Gerade, die durch die Punkte
und die Gerade, die durch die Punkte  und
und 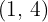 verläuft, begrenzt ist.
verläuft, begrenzt ist.
1 Wir stellen den gegebenen Graphen sowie die Gerade dar und zeichnen die gesuchte Fläche ein
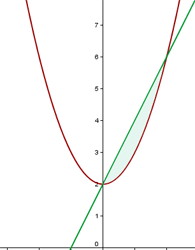
2 Wir berechnen die Steigung der Geraden und ihre entsprechende Gleichung
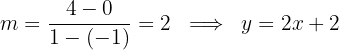
3 Wir berechnen die Integrationsgrenzen. Hierfür ermitteln wir die Punkte, an denen sich die Graphen schneiden
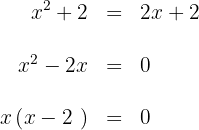
somit sind  und
und  die Integrationsgrenzen.
die Integrationsgrenzen.
4 Die gesuchte Fläche ist durch das Integral der Differenz der beiden Graphen gegeben

5 Wir lösen das bestimmte Integral

Bestimme die Fläche, die durch die Geraden 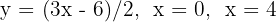 und die x-Achse begrenzt ist.
und die x-Achse begrenzt ist.
1 Wir stellen die gegebenen Geraden graphisch dar und zeichnen die gesuchte Fläche ein
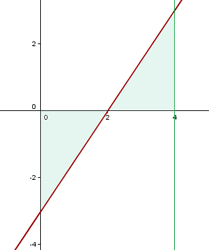
2 Die gesuchte Fläche ist durch den Bereich unterhalb der  -Achse und den Bereich oberhalb dieser Achse gegeben. Der Bereich unterhalb der Achse hat eine negative Fläche, so dass wir den Absolutwert betrachten
-Achse und den Bereich oberhalb dieser Achse gegeben. Der Bereich unterhalb der Achse hat eine negative Fläche, so dass wir den Absolutwert betrachten
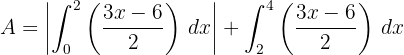
3 Wir lösen das bestimmte Integral
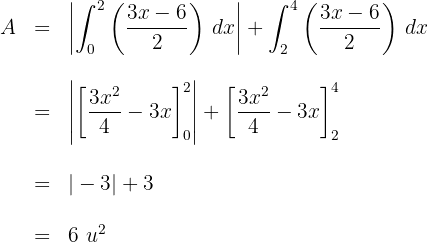
Berechne die Fläche, die durch den Graphen 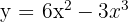 und die x-Achse begrenzt ist.
und die x-Achse begrenzt ist.
1 Wir stellen den gegebenen Graphen graphisch dar und zeichnen die gesuchte Fläche ein
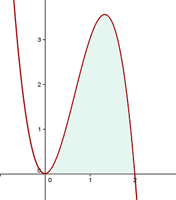
2 Wir berechnen die Integrationsgrenzen. Hierfür ermitteln wir die Punkte, an denen der Graph die x-Achse schneidet.

somit sind  und
und  die Integrationsgrenzen.
die Integrationsgrenzen.
3 Die gesuchte Fläche ist durch folgendes Integral gegeben

4 Wir lösen das bestimmte Integral
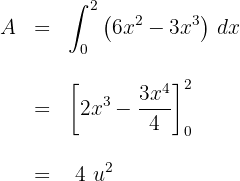
Bestimme den Flächeninhalt des Bereichs der Ebene, der durch die Graphen 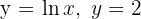 und die Koordinatenachsen begrenzt ist.
und die Koordinatenachsen begrenzt ist.
1 Wir stellen die gegebenen Graphen grafisch dar und zeichnen die gesuchte Fläche ein
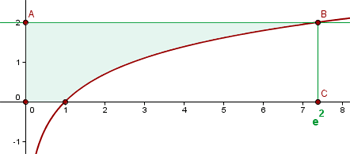
2 Die Fläche ist durch folgendes Integral gegeben

Aus der grafischen Darstellung ergibt sich, dass wenn wir in Bezug auf die Variable  integrieren, die Berechnung einfacher wird. Hierfür drücken wir den Graphen in Funktion von
integrieren, die Berechnung einfacher wird. Hierfür drücken wir den Graphen in Funktion von  aus:
aus:
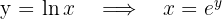
und die gesuchte Fläche ist
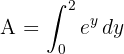
3 Wir lösen das bestimmte Integral
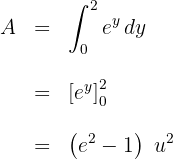
Berechne die Fläche des Bereichs der Ebene, der durch den Kreis 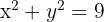 begrenzt ist.
begrenzt ist.
1 Wir stellen den gegebenen Graphen grafisch dar. Wir stellen fest, dass die gesuchte Fläche dem Vierfachen der im 1. Quadranten befindlichen Fläche entspricht
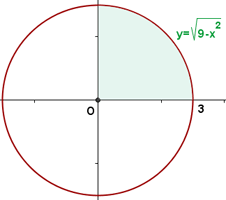
2 Wir drücken den Teil des Kreises, der im 1. Quadranten liegt, in Funktion von  aus
aus
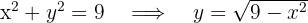
3 Die gesuchte Fläche ist gegeben durch
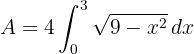
4 Wir lösen das bestimmte Integral. Hierfür wenden wir die trigonometrische Substitution 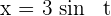 an, deren Differential
an, deren Differential 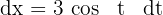 ist. Die Integrationsgrenzen sind:
ist. Die Integrationsgrenzen sind:
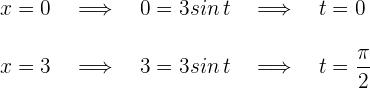
Wir ersetzen die Werte von 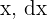 durch
durch 
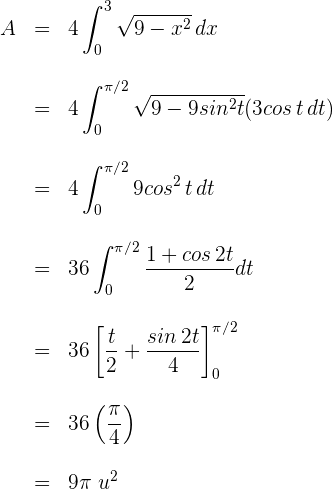
Ermittle die Fläche einer Ellipse mit den Halbachsen  und
und  .
.
1 Wir stellen die Ellipse, deren Mittelpunkt im Ursprung liegt, mit den gegebenen Halbachsen dar
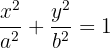
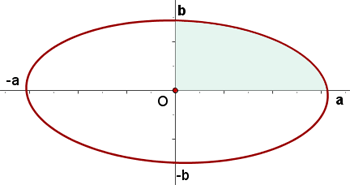
Wir stellen fest, dass die gesuchte Fläche dem Vierfachen der im ersten Quadranten befindlichen Fläche entspricht
2 Wir drücken den Teil der Ellipse, der im 1. Quadranten liegt, in Funktion von  aus
aus

3 Die gesuchte Fläche ist gegeben durch

4 Wir lösen das bestimmte Integral. Hiefür wenden wir die trigonometrische Substitution 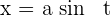 an, deren Differential
an, deren Differential  ist. Die Integrationsgrenzen sind:
ist. Die Integrationsgrenzen sind:
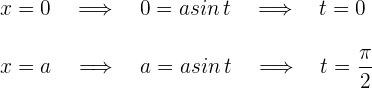
Wir ersetzen die Werte von 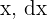 durch
durch 
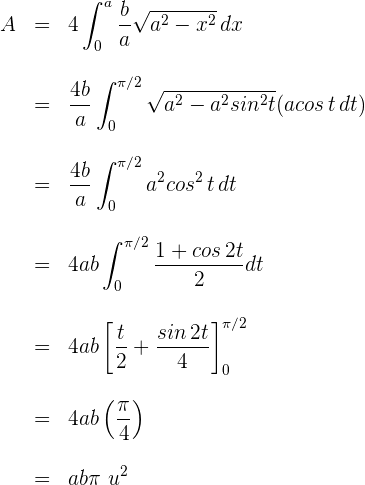
Berechne die Fläche des Bereichs der Ebene, der durch die Nullstellen des Graphen 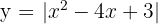 und die
und die  -Achse begrenzt ist.
-Achse begrenzt ist.
1 Wir stellen den Graphen analytisch und grafisch dar. Anschließend können wir die gesuchte Fläche einzeichnen

somit sind  und
und  die Nullstellen des Graphen
die Nullstellen des Graphen
3 Die gesuchte Fläche ist gegeben durch
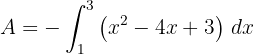
4 Wir lösen das bestimmte Integral
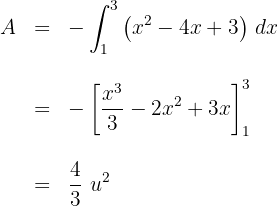
Bestimme die Fläche, die durch 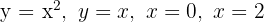 begrenzt ist.
begrenzt ist.
1 Wir stellen den Graphen analytisch und grafisch dar. Anschließend zeichnen wir die gesuchte Fläche ein
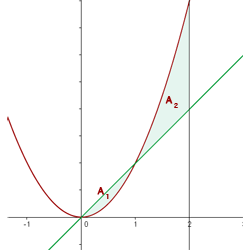
2 Wir berechnen den Schnittpunkt der Geraden mit der Parabel
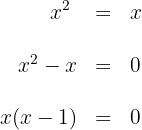
somit sind  und
und  die Koordinaten auf den Achsen, an denen sich die beiden Graphen schneiden
die Koordinaten auf den Achsen, an denen sich die beiden Graphen schneiden
3 Die gesuchte Fläche ist in zwei Teilen gegeben. Im ersten Teil liegt die Gerade oberhalb der Parabel und im zweiten Teil liegt die Parabel oberhalb der Geraden

Somit ist die gesuchte Fläche gegeben durch
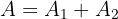
4 Wir lösen die bestimmten Integrale

Ermittle die Fläche der Ebene, die durch die Parabel 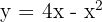 und die Tangenten des Graphen an den Schnittpunkten mit der
und die Tangenten des Graphen an den Schnittpunkten mit der  -Achse begrenzt ist.
-Achse begrenzt ist.
1 Wir ermitteln den Schnittpunkt mit der  -Achse
-Achse
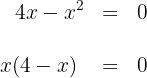
 und
und  sind also die Nullstellen und die Schnittpunkte lauten deshalb
sind also die Nullstellen und die Schnittpunkte lauten deshalb 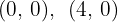 .
.
2 Wir ermitteln die Gleichung der Tangente bei 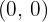

Wir bestimmen die Tangentengleichung bei 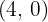

Die beiden Geraden schneiden sich bei 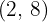
3 Wir stellen den Graphen mit den Tangenten grafisch dar und zeichnen die gesuchte Fläche ein
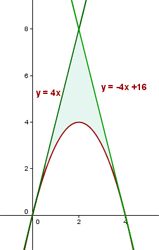
4 Die gesuchte Fläche ist in zwei Teilen gegeben. Im ersten Teil liegt die Gerade mit positiver Steigung oberhalb der Parabel und im zweiten Teil liegt die Gerade mit negativer Steigung oberhalb der Parabel
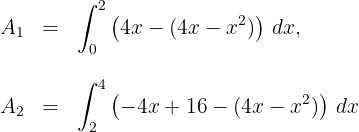
Die gesuchte Fläche ist somit gegeben durch
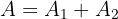
5 Wir lösen die bestimmten Integrale
Mit KI zusammenfassen:












