Kapitel

Definition der Integration rationaler Funktionen
Bie der Integration rationaler Funktionen geht es um die Bestimmung des Integrals  , wobei
, wobei  und
und 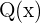 Polynome sind.
Polynome sind.
Zunächst nehmen wir an, dass der Grad von  kleiner ist als der von
kleiner ist als der von 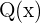 , da er sonst dividiert werden würde.
, da er sonst dividiert werden würde.

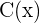 ist der Quotient und
ist der Quotient und  ist der Rest der Polynomdivision.
ist der Rest der Polynomdivision.
Sobald wir wissen, dass der Nenner einen höheren Grad als der Zähler hat, zerlegen wir den Nenner in Faktoren.
Abhängig von den Nullstellen des Nenners ergeben sich die folgenden Fälle:
Der Nenner hat nur einfache reelle Nullstellen
Nullstellen bedeuten, dass es Linearfaktoren gibt, die nicht wiederholt werden. Das heißt, 
Der Bruch 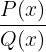 kann wie folgt geschrieben werden:
kann wie folgt geschrieben werden:
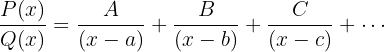
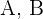 und
und  sind Zahlen, die man erhält, indem man addiert und die Koeffizienten identifiziert oder
sind Zahlen, die man erhält, indem man addiert und die Koeffizienten identifiziert oder  Werte zuweist.
Werte zuweist.
Beispiel
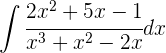
Da der Grad des Nenners kleiner ist als der Grad des Zählers, zerlegen wir zunächst den Nenner in Faktoren
Wir addieren:
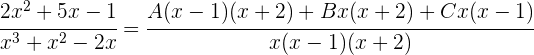
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:

Wir berechnen die Koeffizienten von 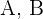 und
und  , und erhalten so die Werte von
, und erhalten so die Werte von  für die der Nenner 0 wird.
für die der Nenner 0 wird.
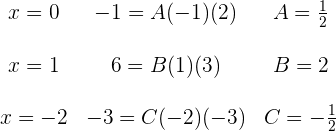
Wir berechnen die Integrale der Brüche:
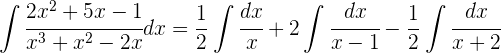
Wir substituieren  ,
, 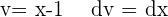 und
und , um schließlich das Integral anzuwenden:
, um schließlich das Integral anzuwenden: 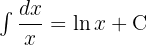
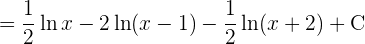
Eine andere Möglichkeit, die Koeffizienten zu ermitteln, besteht darin, die Rechenoperationen durchzuführen und die Koeffizienten gleichzusetzen.
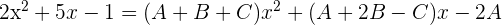
Wir setzen die Koeffizienten gleich:
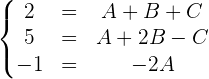
Wir lösen das System und bestimmen den Wert für 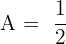 . Diesen setzen wir in die ersten beiden Gleichungen ein und erhalten:
. Diesen setzen wir in die ersten beiden Gleichungen ein und erhalten:
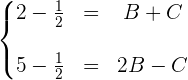
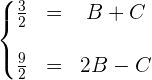
Wir erhalten die Werte  und
und 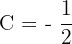 .
.
Der Nenner hat einfache reelle Nullstellen mit Wiederholung
In diesem Fall könnten wir Faktoren der folgenden Form haben:

Der Bruch 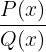 kann wie folgt geschrieben werden:
kann wie folgt geschrieben werden:
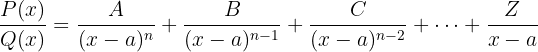
 und
und  sind Zahlen, die man erhält, indem man addiert und die Koeffizienten identifiziert oder
sind Zahlen, die man erhält, indem man addiert und die Koeffizienten identifiziert oder  Werte zuweist.
Werte zuweist.
Beispiel

Da der Grad des Nenners kleiner ist als der Grad des Zählers, zerlegen wir zunächst den Nenner in Faktoren
Wir addieren:

Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
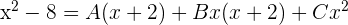
Calculamos los coeficientes de 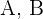 y
y  realizando las operaciones e igualando coeficientes.
realizando las operaciones e igualando coeficientes.

Igualamos coeficientes:
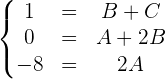
Resolviendo el sistema encontramos el valor de  . Wir setzen in die 2. Gleichung ein und erhalten:
. Wir setzen in die 2. Gleichung ein und erhalten:
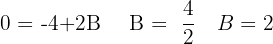
Para finalmente, encontrar el valor de C:
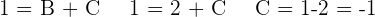 .
.
Wir berechnen die Integrale der Brüche:
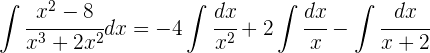
Das 1. Integral ist ein Integral mit Potenzen. Wir substituieren für das 2. und 3. Integral 1er integral es una integral de potencias y haciendo cambios de variables respectivamente para la 2da y 3er integral  und
und  , um schließlich die Integrale anzuwenden:
, um schließlich die Integrale anzuwenden: 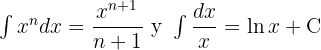
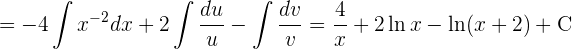
Der Nenner hat mehrfache und einfache Nullstellen
In diesem Fall haben wir Faktoren der Form:
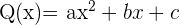
Der Bruch 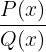 kann wie folgt geschrieben werden:
kann wie folgt geschrieben werden:
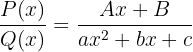
 und
und  sind zu ermittelnde Zahlen.
sind zu ermittelnde Zahlen.
Beispiel

Da der Grad des Nenners kleiner ist als der Grad des Zählers, zerlegen wir zunächst den Nenner in Faktoren

Wir addieren:
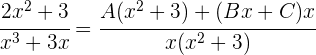
Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
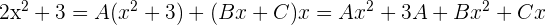
Wir berechnen die Koeffizienten von 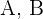 und
und  , indem wir die Berechnungen durchführen und die Koeffizienten gleichsetzen.
, indem wir die Berechnungen durchführen und die Koeffizienten gleichsetzen.
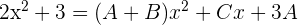
Wir setzen die Koeffizienten gleich:
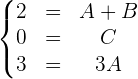
Wir lösen das System und ermitteln den Wert von 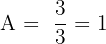 und
und 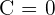 . Nun setzen wir den Wert von A in die 1. Gleichung ein und erhalten:
. Nun setzen wir den Wert von A in die 1. Gleichung ein und erhalten:

Wir berechnen die Integrale der Brüche:
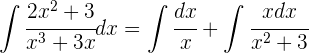
Wir substituieren  und
und 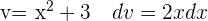 , um schließlich das Integral anzuwenden:
, um schließlich das Integral anzuwenden: 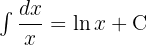
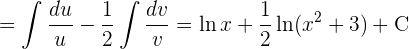
Mit KI zusammenfassen:












