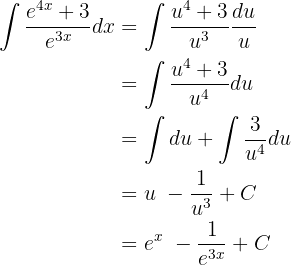Kapitel

Was ist ein Integral und wozu dient es?
Das Integral ist vor allem als Umkehrung der Ableitung bekannt, deren Hauptfunktion die Berechnung der Fläche unter einem Graphen ist, und steht in engem Zusammenhang mit dem Thema Infinitesimalrechnung.
Lustige Tatsache:
Ist dir schon einmal aufgefallen, dass wir beim Lösen eines Integrals immer einen konstanten Wert hinzufügen?
Zum Beispiel: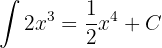
Wenn man darüber nachdenkt, macht das sehr viel Sinn, da die Ableitung einer beliebigen Konstanten  ist. Dies bedeutet, dass wenn wir eine Konstante ableiten, diese verschwindet. Logisch ist also, dass wenn wir die umgekehrten Schritte auf die Ableitung anwenden, das heißt, wenn wir den Wert
ist. Dies bedeutet, dass wenn wir eine Konstante ableiten, diese verschwindet. Logisch ist also, dass wenn wir die umgekehrten Schritte auf die Ableitung anwenden, das heißt, wenn wir den Wert  integrieren, wir als Ergebnis eine Konstante erhalten.
integrieren, wir als Ergebnis eine Konstante erhalten.
Über die Methoden zur Lösung von Integralen
Wie bei den Ableitungen gibt es auch bei den Integralen 2 allgemeine Vorgehensweisen:
1 Durch das Konzept des Grenzwerts
2 Durch Formeln für spezifische Fälle
Man könnte sagen, dass es für jeden Weg, eine Ableitung zu lösen, auch einen Weg gibt, ein Integral zu lösen.
Beispiel:
Gegeben ist die Funktion 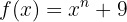
Ihre Ableitung ist 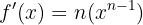 und das Integral wäre
und das Integral wäre 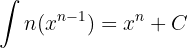
Vorgeschlagene Aufgaben zur Integration
Integriere folgende Funktion:
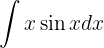
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen

und
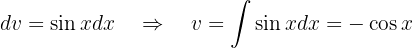
Diese Werte setzen wir in die Formel der partiellen Integration ein und erhalten
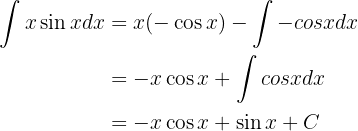
Integriere folgende Funktion
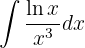
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen
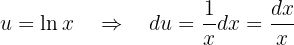
und
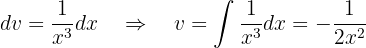
Diese Werte setzen wir in die Formel der partiellen Integration ein und erhalten
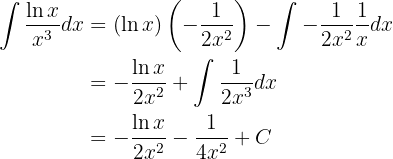
Integriere folgende Funktion
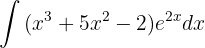
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen
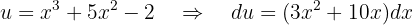
und

Diese Werte setzen wir in die Formel der partiellen Integration ein und erhalten
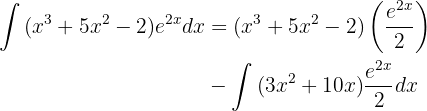
Wir wenden wieder die partielle Integration an, um zu integrieren

in diesem Fall sind  und
und 

und
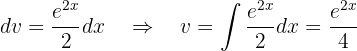
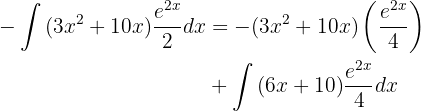
Zum Schluss wenden wir wieder die partielle Integration, um zu integrieren

in diesem Fall sind  und
und 
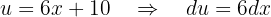
und
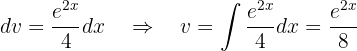
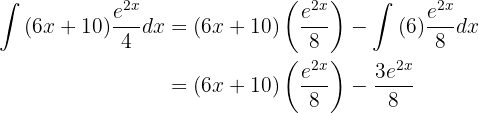
Wir setzen dies in unser 1. Integral ein und erhalten
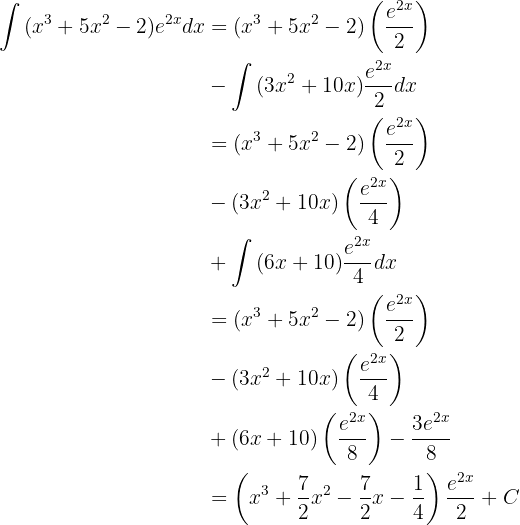
Integriere folgende Funktion
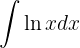
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen
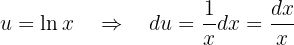
und
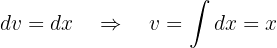
Wir setzen diese Werte in die Formel der partiellen Integration ein und erhalten
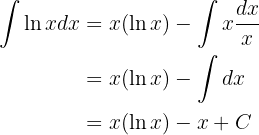
Integriere folgende Funktion
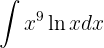
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen
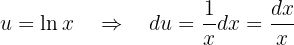
und
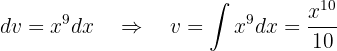
Wir setzen diese Werte in die Formel der partiellen Integration ein und erhalten
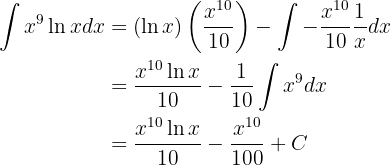
Integriere folgende Funktion
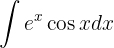
Wir integrieren diese Funktion partiell.
Das heißt:

Wir entscheiden, welcher Teil der Funktion  und welcher
und welcher  sein wird. Wir nehmen
sein wird. Wir nehmen

und
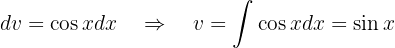
Wir setzen diese Werte in die Formel der partiellen Integration ein und erhalten
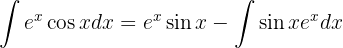
Wir wenden erneut die partielle Integration an, um zu integrieren
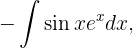
in diesem Fall sind  und
und 

und
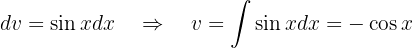
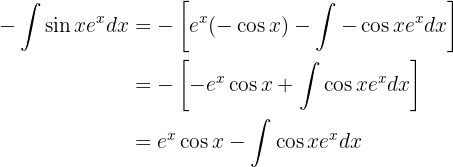
Wenn wir all das in unser 1. Integral einsetzen, erscheint das Integral, das wir auf der rechten und linken Seite berechnen möchten, mit negativem Vorzeichen. Wir müssen also nur das Integral bestimmen, das wir ermitteln möchten
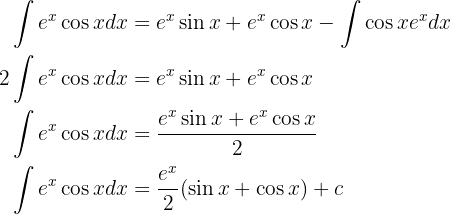
Integriere folgende Funktion
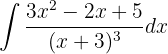
Um diese Funktion zu integrieren, müssen wir sie zunächst vereinfachen

Zur Vereinfachung auf einen leicht zu integrierenden Ausdruck wenden wir Partialbrüche an. Die Theorie der Partialbrüche wird nicht im Detail erklärt, aber es soll versucht werden, jeden Schritt genau zu beschreiben.
Da der Nenner ein Polynom der 1. Ordnung zur dritten Potenz ist, kann unser Ausdruck im Allgemeinen wie folgt geschrieben werden
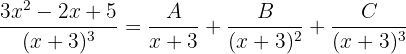
Für bestimmte reelle Zahlen  ,
,  und
und  muss man, um die Werte dieser Unbekannten zu bestimmen, diese addieren und dann die Koeffizienten der Terme gleichen Grades gleichsetzen, d. h.
muss man, um die Werte dieser Unbekannten zu bestimmen, diese addieren und dann die Koeffizienten der Terme gleichen Grades gleichsetzen, d. h.
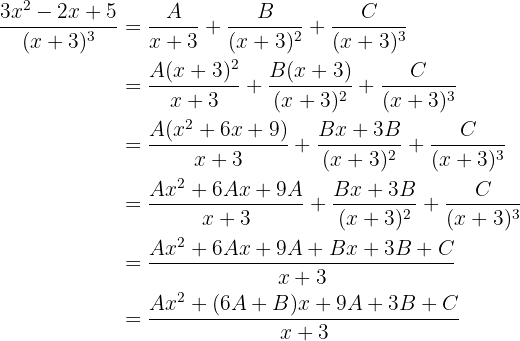
daraus folgt, dass
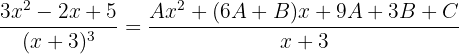
Die Zähler sind deshalb gleich
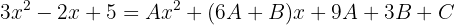
und die Koeffizienten der Terme gleichen Grades sind ebenfalls gleich. Das heißt

Die 1. Ungleichung ergibt direkt 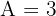 . Wir setzen den Wert für
. Wir setzen den Wert für  in die 2. Ungleichung ein und erhalten
in die 2. Ungleichung ein und erhalten
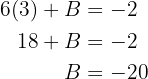
Wir setzen den Wert für 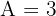 und
und  in die 3. Ungleichung ein und erhalten
in die 3. Ungleichung ein und erhalten
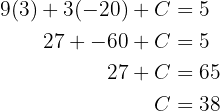
Unsere Funktion entspricht somit

Nun können wir mit der Integration fortfahren. Wir verwenden den Variablentausch wie folgt

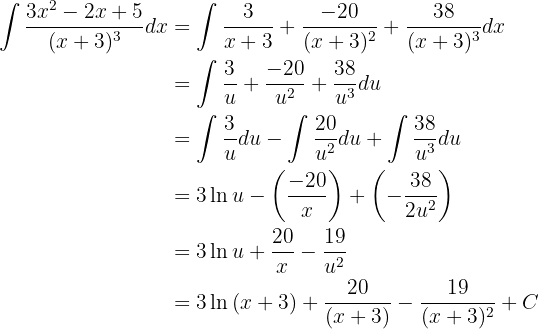
Integriere folgende Funktion

Wir integrieren mit der Methode des Variablentauschs. Wir nehmen
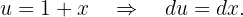
Wir stellen außerdem fest, dass  . Somit können wir in das ursprüngliche Integral einsetzen
. Somit können wir in das ursprüngliche Integral einsetzen
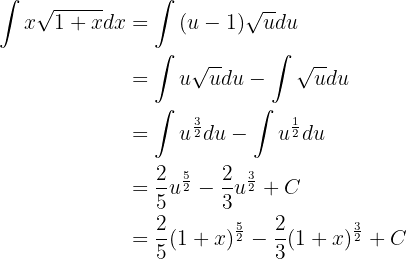
Integriere folgende Funktion
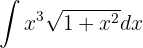
Wir integrieren mit der Methode des Variablentauschs. Wir nehmen
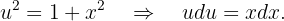
Wir stellen außerdem fest, dass  . Somit können wir in das ursprüngliche Integral einsetzen
. Somit können wir in das ursprüngliche Integral einsetzen
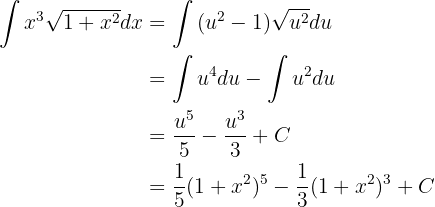
Integriere folgende Funktion
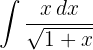
Wir integrieren mit der Methode des Variablentauschs. Wir nehmen
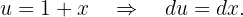
Wir stellen außerdem fest, dass  . Somit können wir in das ursprüngliche Integral einsetzen
. Somit können wir in das ursprüngliche Integral einsetzen
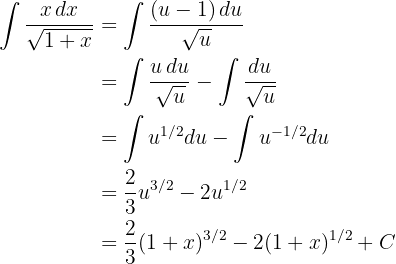
Integriere folgende Funktion
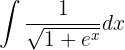
Wir integrieren mit der Methode des Variablentauschs. Wir nehmen

Nun bestimmen wir die Differentiale
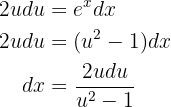
Somit können wir in das ursprüngliche Integral einsetzen
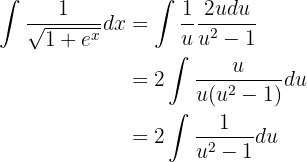
Wir wenden Partialbrüche an, um diesen Bruch zu vereinfachen und ihn als Summe von Brüchen auszudrücken, die leicht zu integrieren ist. Wir erhalten
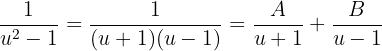
Wir berechnen die letzte Summe und erhalten
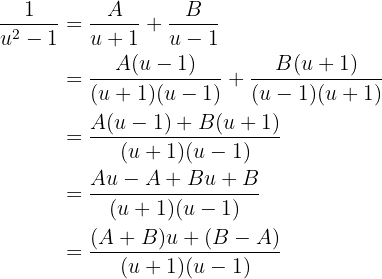
Indem wir die Zähler gleichsetzen, erhalten wir 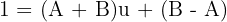 , woraus direkt folgt, dass
, woraus direkt folgt, dass

Wir stellen fest, dass aus der 1. Ungleichung direkt folgt, dass  und aus der 2. ergibt sich
und aus der 2. ergibt sich 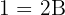 , weshalb
, weshalb

Und somit
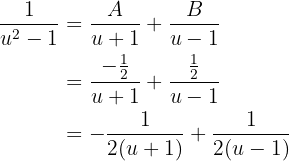
Dies setzen wir in das Integral ein

Daraus folgt, dass wenn wir den Wert von  durch
durch  ersetzen, also
ersetzen, also 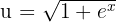 , Folgendes erhalten
, Folgendes erhalten
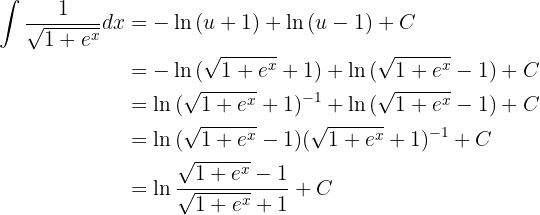
Integriere folgende Funktion
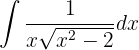
Wir integrieren mit der trigonometrischen Substitution und nehmen
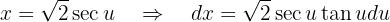
Diese Werte setzen wir in das Integral ein
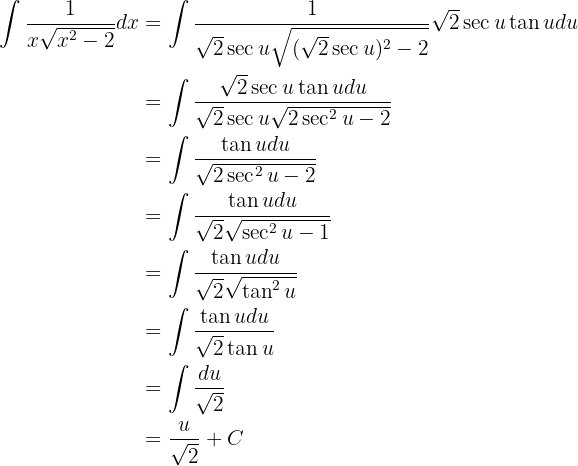
Wenn wir nun substituieren, nehmen wir  und können so
und können so  bestimmten
bestimmten
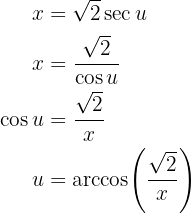
wir substituieren und erhalten
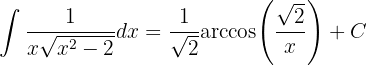
Integriere folgende Funktion
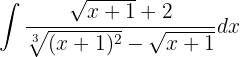
Wir integrieren mit der Methode des Variablentauschs und nehmen
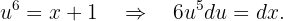
Wir setzen diese Werte in das Integral ein und erhalten
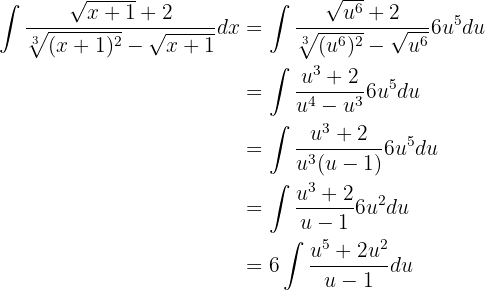
Nun können wir den Ausdruck innerhalb des Integrals mit der Partialbruchzerlegung vereinfachen. Wir erhalten
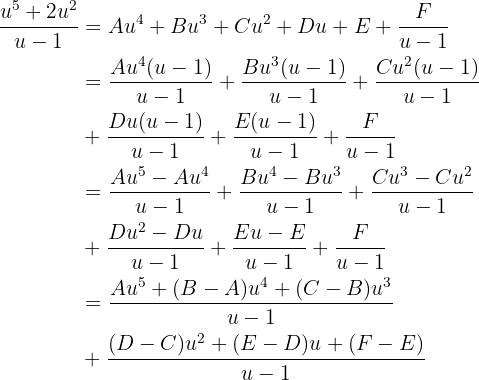
Dadurch erhalten wir folgendes Gleichungssystem
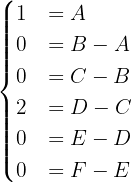
Daraus ergibt sich, dass 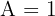 ,
,  ,
, 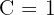 ,
,  ,
, 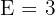 und
und 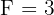 . Unser Ausdruck ist somit
. Unser Ausdruck ist somit
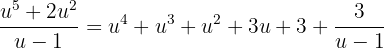
Wir setzen in das ursprüngliche Integral ein und erhalten
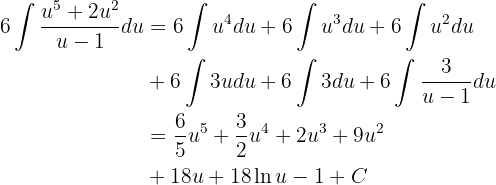
Nun müssen wir den Ausdruck nur noch in Bezug auf  schreiben. Wir nehmen
schreiben. Wir nehmen 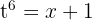 und erhalten somit
und erhalten somit 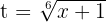 . Schließlich substituieren wir
. Schließlich substituieren wir
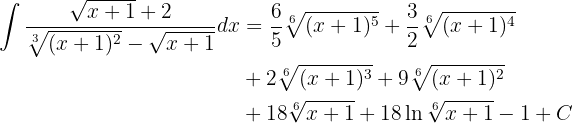
Integriere folgende Funktion
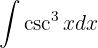
Wir integrieren mit der Methode des Variablentauschs und nehmen
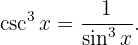
Unser Variablentausch ist
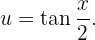
Daraus ergibt sich, dass
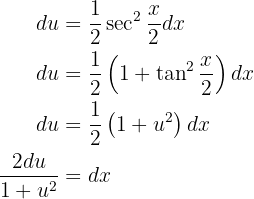
Da wir im Integral 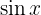 haben, müssen wir diese Funktion in Bezug auf
haben, müssen wir diese Funktion in Bezug auf 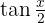 schreiben, um die Funktion in Bezug auf
schreiben, um die Funktion in Bezug auf  zu substituieren. Wir erinnern uns an folgende trigonomische Identität
zu substituieren. Wir erinnern uns an folgende trigonomische Identität
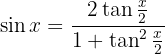
und somit
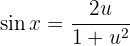
Wir setzen in das ursprüngliche Integral ein und erhalten
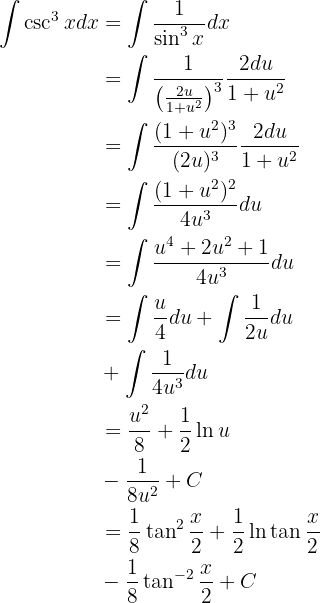
Integriere folgende Funktion
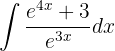
Wir integrieren mit der Methode des Variablentauschs und nehmen
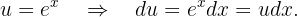
Aus dem Differential ergibt sich, dass  . Wir setzen nun in unser ursprüngliches Integral ein und erhalten
. Wir setzen nun in unser ursprüngliches Integral ein und erhalten