Ermittle das Volumen des Kegelstumpfes, der durch Rotation um  und die durch
und die durch 
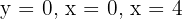 begrenzte Fläche entsteht.
begrenzte Fläche entsteht.
Ein Kegelstumpf wird durch einen Umfang in Abhängigkeit von einem Parameter bestimmt. In diesem Fall ist der Radius eines solchen Kreises durch  gegeben und der Parameter
gegeben und der Parameter  liegt zwischen
liegt zwischen  . Der Flächeninhalt eines Kreises ist
. Der Flächeninhalt eines Kreises ist  mal dem Radius zum Quadrat. Angesichts der Grenzen der Aussage und der Tatsache, dass wir das Volumen eines Stumpfes ermitteln möchten, müssen wir das Integral der Fläche eines Kreises mit dem Radius
mal dem Radius zum Quadrat. Angesichts der Grenzen der Aussage und der Tatsache, dass wir das Volumen eines Stumpfes ermitteln möchten, müssen wir das Integral der Fläche eines Kreises mit dem Radius  ermitteln, d. h.
ermitteln, d. h.
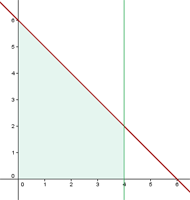
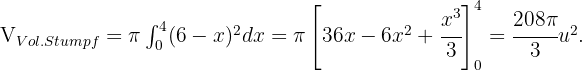
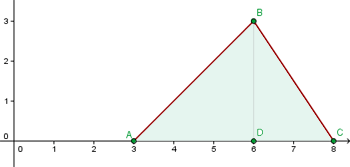
Berechne das Volumen eines Dreiecks mit den Eckpunkten  bei einer Drehung von
bei einer Drehung von 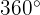 um die x-Achse.
um die x-Achse.
Zunächst müssen wir die Geraden bestimmen, die das Dreieck bilden. Die erste von ihnen ist durch den Punkt 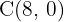 gegeben. Die beiden folgenden sind gegeben durch: Gleichung der Geraden, die durch
gegeben. Die beiden folgenden sind gegeben durch: Gleichung der Geraden, die durch 
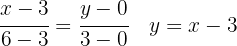 verläuft. Gleichung der Geraden, die durch
verläuft. Gleichung der Geraden, die durch 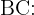
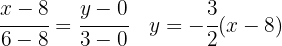 verläuft. Da wir dieses Dreieck drehen werden, wird das Volumen durch die Fläche eines Kreises bestimmt. Und wir müssen bedenken, dass diese Radien von den oben berechneten Geraden abhängen. Zuerst geht
verläuft. Da wir dieses Dreieck drehen werden, wird das Volumen durch die Fläche eines Kreises bestimmt. Und wir müssen bedenken, dass diese Radien von den oben berechneten Geraden abhängen. Zuerst geht  von
von  nach
nach  mit der Geraden
mit der Geraden  und dann von
und dann von  nach
nach  mit der Geraden
mit der Geraden  . Abschließend sei daran erinnert, dass die Fläche eines Kreises
. Abschließend sei daran erinnert, dass die Fläche eines Kreises  mal dem Radius zum Quadrat entspricht. Somit ist das Volumen:
mal dem Radius zum Quadrat entspricht. Somit ist das Volumen:
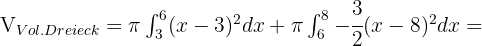
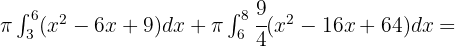



Berechne das Volumen des Kegelstumpfes, der durch das Trapez gebildet wird, das durch die Abszissenachse, die Gerade 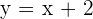 und die Koordinaten
und die Koordinaten  und
und 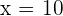 begrenzt wird, wenn es sich um die x-Achse dreht.
begrenzt wird, wenn es sich um die x-Achse dreht.
Wir haben einen Kegelstumpf, der durch Drehung des durch 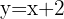 und
und 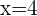 begrenzten Trapezes entsteht,
begrenzten Trapezes entsteht, 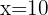 . Das Volumen dieses Trapezes erhält man durch das Integral des Flächeninhalts eines Kreises mit dem Radius
. Das Volumen dieses Trapezes erhält man durch das Integral des Flächeninhalts eines Kreises mit dem Radius 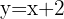 . Zur Erinnerung: Der Flächeninhalt eines Kreises ist
. Zur Erinnerung: Der Flächeninhalt eines Kreises ist  mal dem Radius zum Quadrat.
mal dem Radius zum Quadrat. 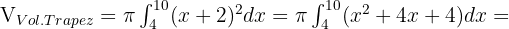
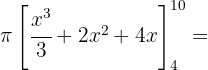
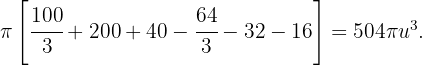
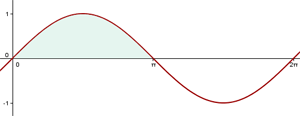
Berechne das Volumen, das von einer Halbwelle der Sinuskurve 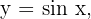 bei einer Drehung um die x-Achse erzeugt wird.
bei einer Drehung um die x-Achse erzeugt wird.
Wir möchten die Funktion 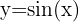 um die x-Achse drehen. Das Volumen dieser Figur ergibt sich aus der Addition der Volumen der Kreise mit dem Radius
um die x-Achse drehen. Das Volumen dieser Figur ergibt sich aus der Addition der Volumen der Kreise mit dem Radius 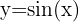 zwischen den Punkten
zwischen den Punkten  und
und  . Der Flächeninhalt eines Kreises ist
. Der Flächeninhalt eines Kreises ist  mal dem Radius zum Quadrat. Somit
mal dem Radius zum Quadrat. Somit 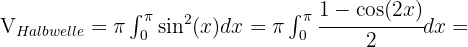
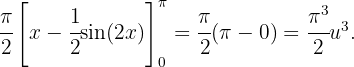
Berechne das Volumen, das durch die Drehung des durch die Graphen von 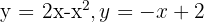 begrenzten Raums um die x-Achse entsteht.
begrenzten Raums um die x-Achse entsteht.
Um den Bereich zu finden, der durch die Graphen der Funktionen 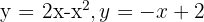 begrenzt wird, müssen wir zunächst die Schnittpunkte dieser Graphen finden, die die Integrationsgrenzen bestimmen.
begrenzt wird, müssen wir zunächst die Schnittpunkte dieser Graphen finden, die die Integrationsgrenzen bestimmen. 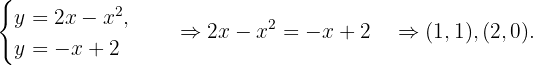 Die Fläche des Bereichs ist die Fläche einer Scheibe, die durch Subtraktion der Flächen zweier Kreise bestimmt wird, von denen der erste den Radius
Die Fläche des Bereichs ist die Fläche einer Scheibe, die durch Subtraktion der Flächen zweier Kreise bestimmt wird, von denen der erste den Radius  und der zweite Kreis den Radius
und der zweite Kreis den Radius
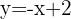 hat. Der Flächeninhalt eines Kreises ist
hat. Der Flächeninhalt eines Kreises ist  mal dem Radius
mal dem Radius
zum Quadrat. Somit
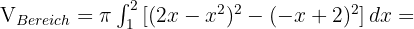
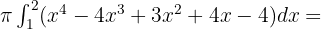

Berechne das Volumen des Rotationskörpers, der durch die Drehung um die x-Achse, den Bereich, der durch die Funktion  bestimmt wird, die Abszissenachse und die Geraden
bestimmt wird, die Abszissenachse und die Geraden  und
und  entsteht.
entsteht.
Man beachte, dass dieses Volumen durch das Integral ermittelt wird. Zunächst sind die Integrationsgrenzen  und
und  . Zweitens: Die Funktion, die wir integrieren wollen, ist die Fläche eines Kreises mit dem Radius
. Zweitens: Die Funktion, die wir integrieren wollen, ist die Fläche eines Kreises mit dem Radius  . Der Flächeninhalt eines Kreises ist
. Der Flächeninhalt eines Kreises ist  mal dem Radius zum Quadrat. Somit
mal dem Radius zum Quadrat. Somit 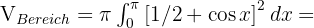
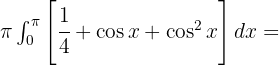
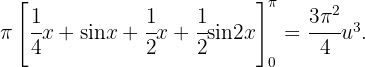
Berechne das Volumen des Körpers, der durch die Drehung des durch die Graphen von 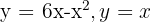 begrenzten Raums um die x-Achse entsteht.
begrenzten Raums um die x-Achse entsteht.
Zunächst bestimmen wir die Schnittpunkte dieser beiden Graphen, die 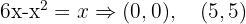 sind. Nun zeichnen wir den Bereich, den wir drehen möchten
sind. Nun zeichnen wir den Bereich, den wir drehen möchten
Die Parabel liegt oberhalb der Geraden im Integrationsintervall.
Man beachte, dass die Fläche dieser Region die Fläche einer Scheibe ist, die man erhält, wenn man die Fläche
Man beachte, dass die Fläche dieser Region die Fläche einer Scheibe ist, die man erhält, wenn man die Fläche zweier Kreise jeweils mit den Radien 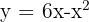 und
und  subtrahiert.
subtrahiert.
Der Flächeninhalt eines Kreises ist  mal dem Radius zum Quadrat, also
mal dem Radius zum Quadrat, also
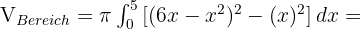
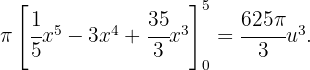
Berechne das Volumen des Kreises  bei einer Drehung um die x-Achse.
bei einer Drehung um die x-Achse.
Zuerst schreiben wir die Gleichung des Kreises um und erhalten dann seinen Radius und seinen Mittelpunkt 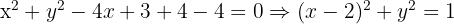 .
.
Der Mittelpunkt des Kreises ist  und der Radius
und der Radius 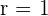 .
.
Schnittpunkte mit der x-Achse:
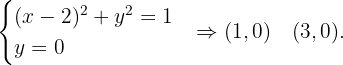
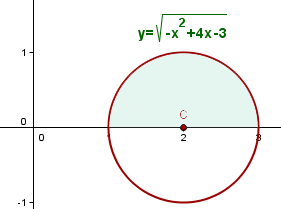
Mit diesen Informationen können wir das Volumen des Bereichs berechnen, das wie folgt lautet: 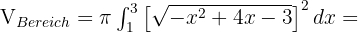
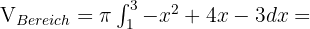
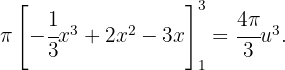
Berechne das Volumen der Figur, die durch die Drehung der Ellipse
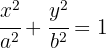
um die x-Achse entsteht.
Aus der Gleichung der Ellipse ergibt sich die Funktion, die den Bereich bestimmt, für den wir das Volumen ermitteln müssen: 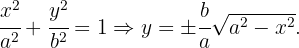
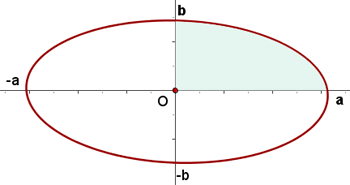
Da es sich bei der Ellipse um eine symmetrische Kurve handelt, ist das gesuchte Volumen 2 mal so groß wie das Volumen,
das durch den Bogen 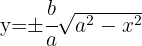 zwischen
zwischen  und
und  entsteht.
entsteht. 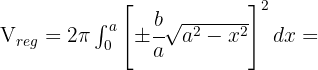
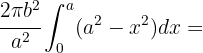
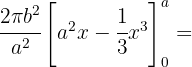
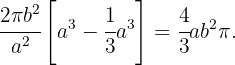
Mit KI zusammenfassen:


