Kapitel

Löse die folgenden Integrale mit Potenzen:
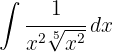
Um das Integral zu lösen, erhöhen wir den Nenner und vereinfachen die Potenzen. Dann wenden wir das unmittelbare Integral von Potenzen an, d. h.  .
.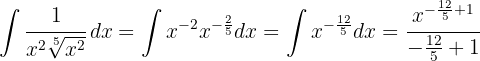
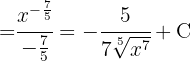
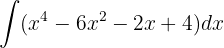
Wir beginnen mit der Trennung des Integrals und wenden die entsprechenden unmittelbaren Integrale an, d. h,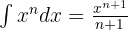 y
y 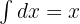 .
. 
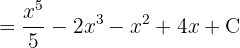

Wir trennen das Integral in zwei Teile, wandeln die Wurzel in eine Potenz um und wenden schließlich das Integral einer Potenz an 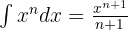
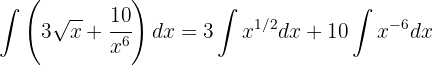
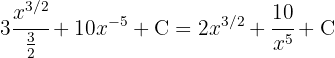
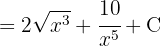

Wir beginnen mit der Trennung des Integrals und der Vereinfachung der Ausdrücke und wenden schließlich das Integral einer Potenz an 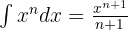

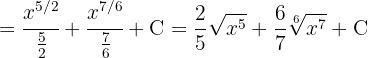

Wir beginnen mit der Trennung des Integrals und wenden das unmittelbare Integral einer Potenz an 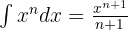
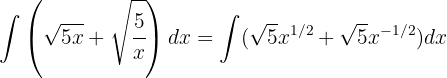


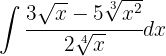
Wir trennen das Integral und vereinfachen die Ausdrücke 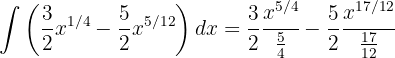
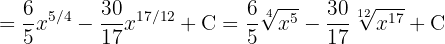
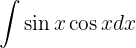
Um das folgende Integral zu lösen, substituieren wir 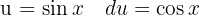

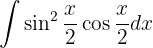
Um das folgende Integral zu lösen, substituieren wir 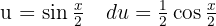

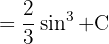
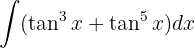
Wir faktorisieren den gemeinsamen Term 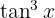 und wenden
und wenden 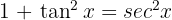 an
an
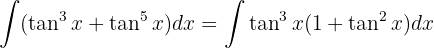
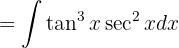 Wir substituieren
Wir substituieren 

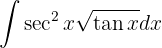
Um das folgende Integral zu lösen, substituieren wir 
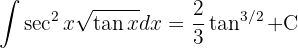
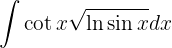
Um das folgende Integral zu lösen, substituieren wir 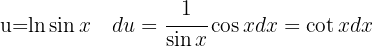 ,
,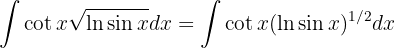
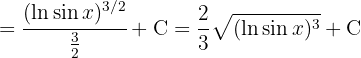
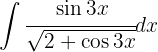
Um das folgende Integral zu lösen, substituieren wir  ,
,
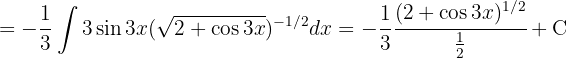
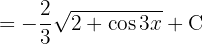

Um das folgende Integral zu lösen, substituieren wir  ,
,
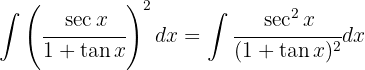

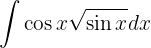
Um das folgende Integral zu lösen, substituieren wir  ,
,
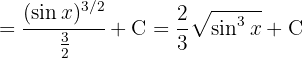
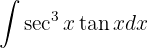
Um das folgende Integral zu lösen, substituieren wir 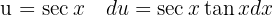 ,
,
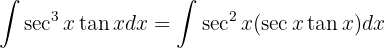

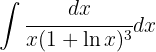
Um das folgende Integral zu lösen, substituieren wir  ,
,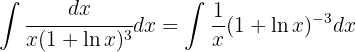
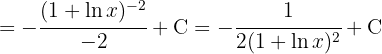

Wir schreiben die Wurzel in ihrer Exponentialform und vereinfachen 
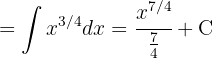


Wir schreiben die Wurzel in ihrer Exponentialform und vereinfachen 


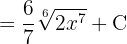
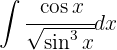
Wir substituieren 
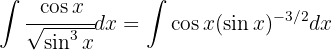


Wir können den Ausdruck wie folgt vereinfachen und substituieren schließlich 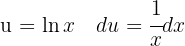

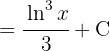

Wir substituieren 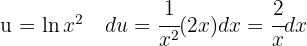
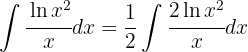


Wir substituieren 
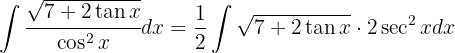
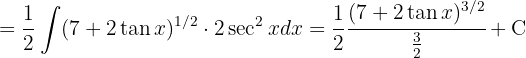
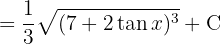
Berechne die Integrale mit Logarithmen:
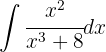
Wir substituieren 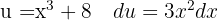 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 

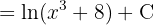
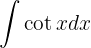
Wir wenden die Definition 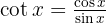 an und substituieren
an und substituieren 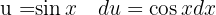 . Schließlich wenden wir das unmittelbare Integral an:
. Schließlich wenden wir das unmittelbare Integral an: 
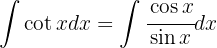
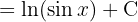

Wir wenden 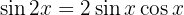 und
und 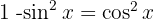 an, vereinfachen, substituieren
an, vereinfachen, substituieren 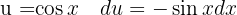 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
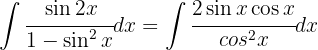

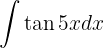
Wir wenden die Definition 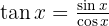 an und substituieren
an und substituieren  . Schließlich wenden wir das unmittelbare Integral an:
. Schließlich wenden wir das unmittelbare Integral an: 
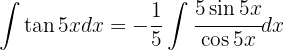
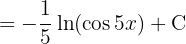
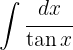
Wir wenden die Definition 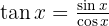 an und substituieren
an und substituieren 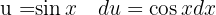 . Schließlich wenden wir das unmittelbare Integral an:
. Schließlich wenden wir das unmittelbare Integral an: 
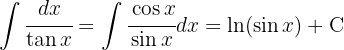

Wir substituieren 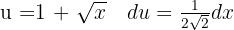 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
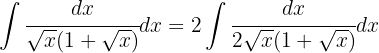
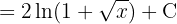
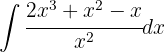
Wir trennen das Integral und wenden die entsprechenden unmittelbaren Integrale an: 
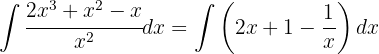
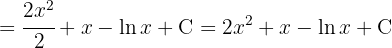
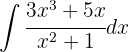
Wir trennen und vereinfachen das Integral, substituieren  und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
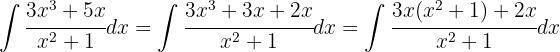

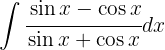
Wir substituieren 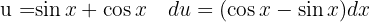 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
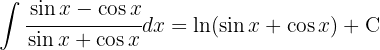

Wir substituieren  und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 


Wir beginnen mit der Definition 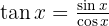 , substituieren
, substituieren 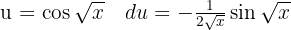 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 


Löse die folgenden Integrale mit Exponenten:
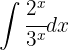
Um das folgende Integral zu lösen, faktorisieren wir den Exponenten und können so das unmittelbare Integral anwenden: 
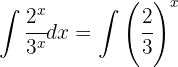
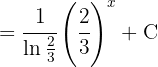
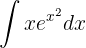
Wir substituieren 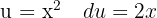 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
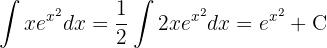
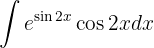
Wir substituieren 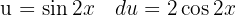 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
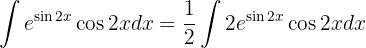
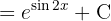
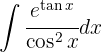
Um das folgende Integral zu lösen, beginnen wir mit der Definition 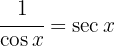 , substituieren
, substituieren 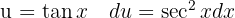 und wenden schließlich das unmittelbare Integral an
und wenden schließlich das unmittelbare Integral an 
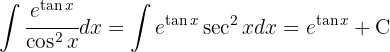

Um das Integral zu lösen, substituieren wir zunächst 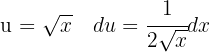 , um das unmittelbare Integral anzuwenden:
, um das unmittelbare Integral anzuwenden: 

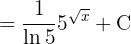
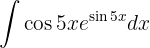
Um das Integral zu lösen, substituieren wir zunächst 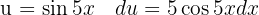 und wenden schließlich das umittelbare Integral an
und wenden schließlich das umittelbare Integral an 
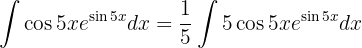
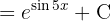

Um das Integral zu lösen, substituieren wir zunächst 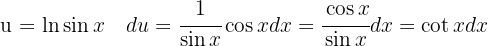 und wenden schließlich das umittelbare Integral an
und wenden schließlich das umittelbare Integral an 


Um das folgende Integral zu lösen, trennen wir das Integral, substituieren entsprechend  und
und  , und wenden schließlich das unmittelbare Integral
, und wenden schließlich das unmittelbare Integral  an
an
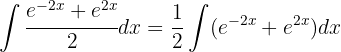
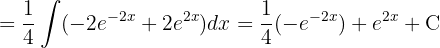
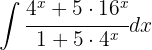
Um das folgende Integral zu lösen, vereinfachen wir zunächst den Ausdruck und wenden das unmittelbare Integral an: 
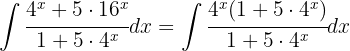
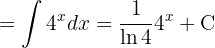
Berechne die folgenden trigonometrischen Integrale:

Um das folgende Integral zu lösen, trennen wir zunächst das Integral und wenden die unmittelbaren Integrale an:  y
y 
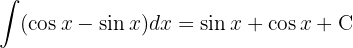

Um das folgende Integral zu lösen, trennen wir zunächst das Integral und wenden die unmittelbaren Integrale an: 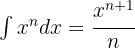 y
y 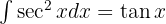
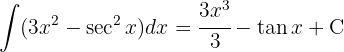
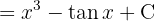
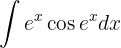
Um das folgende Integral zu lösen, beginnen wir mit der Substitution 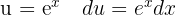 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 

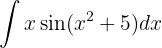
Um das folgende Integral zu lösen, beginnen wir mit der Substitution  und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
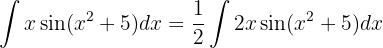
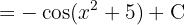

Um das folgende Integral zu lösen, beginnen wir mit der Substitution 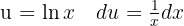 und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
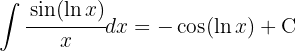
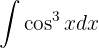
Um das Integral zu lösen, wenden wir 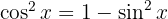 an, trennen die Integrale, substituieren
an, trennen die Integrale, substituieren  und wenden die unmittelbaren Integrale an:
und wenden die unmittelbaren Integrale an:  y
y 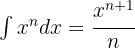

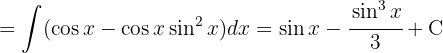

Um das Integral zu lösen, wenden wir  und
und 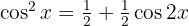 an
an 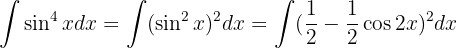
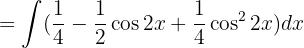
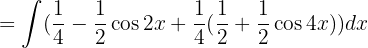
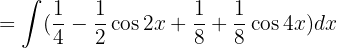

Wir trennen die Integrale und substituieren 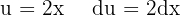 ,
,  und wenden das unmittelbare Integral an:
und wenden das unmittelbare Integral an: 
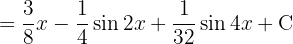
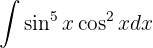
Wir schreiben das Integral wie folgt um:  Wir substituieren
Wir substituieren  und erhalten
und erhalten

Wir erweitern 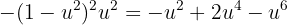
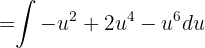

Durch Rücksubstitution erhalten wir


Wir schreiben das Integral wie folgt um: 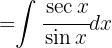
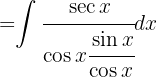

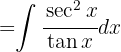
Wir substituieren 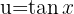 ,
, 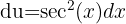 und erhalten
und erhalten
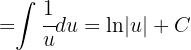
Wir substituieren erneut und erhalten
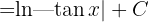
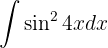
Wir schreiben das Integral wie folgt um: 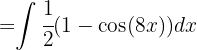

Diese letzten Integrale sind gleich
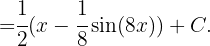
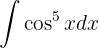
Wir schreiben das Integral wie folgt um:  Wir substituieren
Wir substituieren 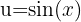 und erhalten
und erhalten 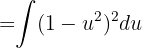
Nun erweitern wir 

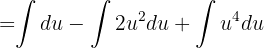
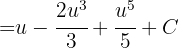
Durch Rücksubstitution erhalten wir
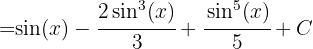

Wir substituieren  und
und  und erhalten
und erhalten 
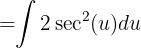
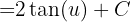
Durch Rücksubstitution erhalten wir

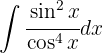
Wir schreiben das Integral wie folgt um:  Wir substituieren
Wir substituieren 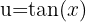 ,
, 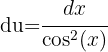 und erhalten
und erhalten
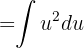
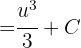
Durch Rücksubstitution erhalten wir
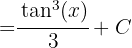
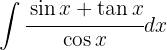
Wir substituieren 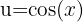 ,
, 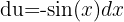 und erhalten
und erhalten 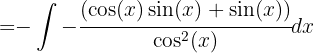
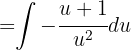
Wir erweitern

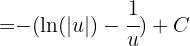
Durch Rücksubstitution erhalten wir
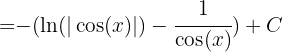
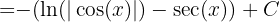
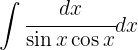
Wir schreiben das Integral wie folgt um: 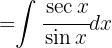
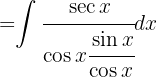

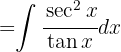
Wir substituieren 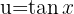 ,
, 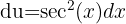 und erhalten
und erhalten
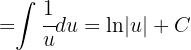
Wir substituieren erneut und erhalten
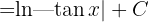
Löse die trigonometrischen Integrale:

Wir nutzen die folgende trigonometrische Identität:  Das Integral hat folgende Form
Das Integral hat folgende Form

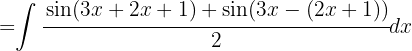
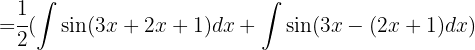
Da
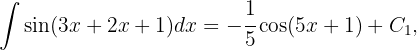
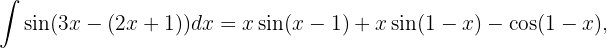
lautet das Ergebnis
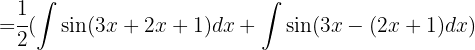
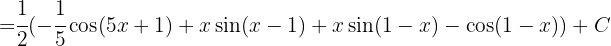

Wir schreiben das Integral wie folgt um: 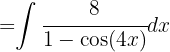

Wir substituieren  ,
,  und erhalten
und erhalten
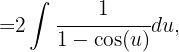
Da
 ,
,
ist das ursprüngliche Integral gleich
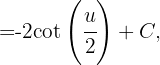
Durch Rücksubstitution erhalten wir
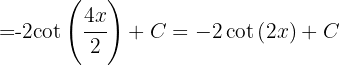
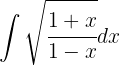
Zunächst substituieren wir 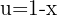 ,
, 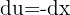 ,
,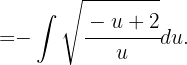 Wir integrieren partiell und erhalten
Wir integrieren partiell und erhalten
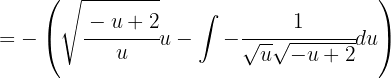
Da
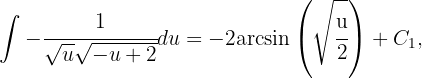
somit
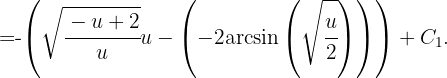
Durch Rücksubstitution erhalten wir
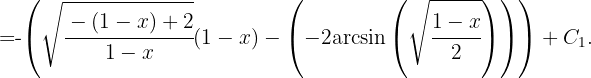


Wir schreiben den Integranden wie folgt um: 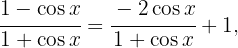 , somit
, somit


Da

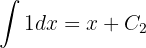
Das ursprüngliche Integral ist gleich
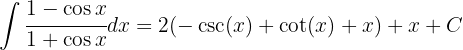
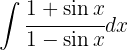
Wir schreiben den Integranden wie folgt um: 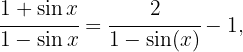 , somit
, somit
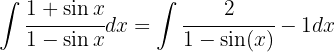
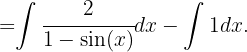
Da

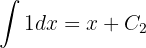
Das ursprüngliche Integral ist gleich

Berechne die Integrale:

Wir wenden folgende trigonometrische Identität an: 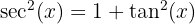 und schreiben das Integral um
und schreiben das Integral um
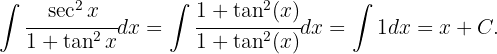
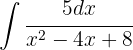
Wir schreiben das Integral wie folgt um: 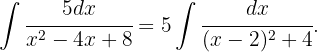 Nun substituieren wir
Nun substituieren wir 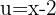 ,
, 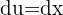 und erhalten
und erhalten
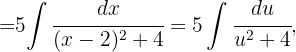
Nun wenden wir das folgende trigonometrische Integral an

Durch Rücksubstitution erhalten wir
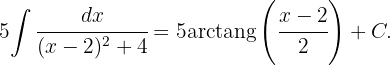

Wir erweitern den Integranden wie folgt: 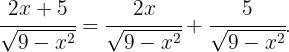 Somit
Somit
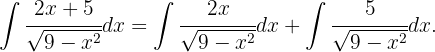
Da
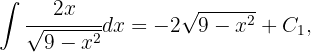
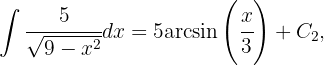
Das ursprüngliche Integral lautet
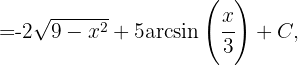

Wir schreiben das Integral wie folgt um:  Nun substituieren wir
Nun substituieren wir 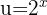 ,
, 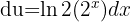 und erhalten
und erhalten

Nun wenden wir das trigonometrische Integral an
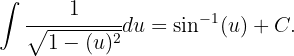
Durch Rücksubstitution erhalten wir
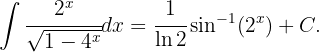
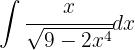
Wir substituieren zunächst 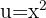 ,
, 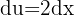 , entonces
, entonces Nun wenden wir das trigonometrische Integral mit
Nun wenden wir das trigonometrische Integral mit  und
und 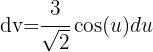 an. Wir erhalten
an. Wir erhalten 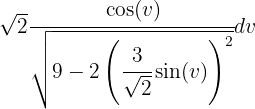
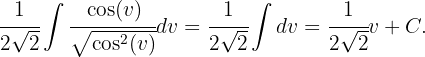
Durch Rücksubstitution erhalten wir
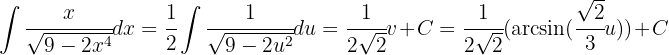


Wir substituieren zunächst 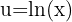 ,
,  und erhalten
und erhalten 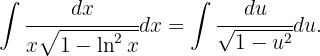 Da
Da

folgt daraus:
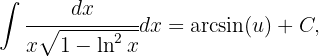
Durch Rücksubstitution erhalten wir
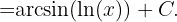
Problemstellungen zu Integralen
Bestimme eine Funktion  , deren Ableitung
, deren Ableitung 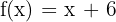 ist und die für
ist und die für  den Wert
den Wert 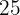 annimmt.
annimmt.
Gegeben ist  Wir nehmen den folgenden Wert für die Konstante
Wir nehmen den folgenden Wert für die Konstante  . Durch den Fundamentalsatz der Analysis erhalten wir
. Durch den Fundamentalsatz der Analysis erhalten wir
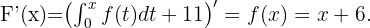
Wir integrieren in  und erhalten
und erhalten
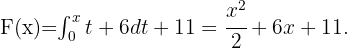
Wir werten für  und erhalten
und erhalten
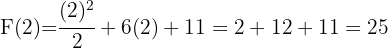
Welche der unendlich vielen Stammfunktionen der Funktion 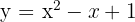 ist diejenige, die für
ist diejenige, die für  den Wert
den Wert  annimmt?
annimmt?
Gegeben ist 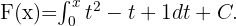 Wir nehmen den folgenden Wert für die Konstante
Wir nehmen den folgenden Wert für die Konstante  . Durch den Fundamentalsatz der Analysis erhalten wir
. Durch den Fundamentalsatz der Analysis erhalten wir
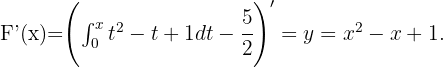
Wir integrieren in  und erhalten
und erhalten
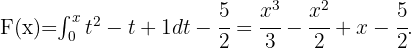
Schließlich werten wir für  aus und erhalten
aus und erhalten
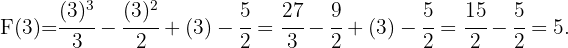
Ermittle eine Gerade, deren Steigung  ist, und die durch den Punkt
ist, und die durch den Punkt 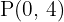 verläuft.
verläuft.
Wir wissen, dass die Punkt-Steigungsform einer Geraden wie folgt gegeben ist:  wobei
wobei  die Steigung der Geraden und
die Steigung der Geraden und  der Schnittpunkt mit der
der Schnittpunkt mit der  -Achse ist. Auch die Ableitung der Funktion, die die Gerade darstellt, ist die Steigung der Geraden. Somit
-Achse ist. Auch die Ableitung der Funktion, die die Gerade darstellt, ist die Steigung der Geraden. Somit
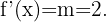
Außerdem wissen wir, dass  und somit
und somit
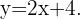
Schreibe eine Stammfunktion funktion von 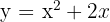 , deren Graph durch den Punkt
, deren Graph durch den Punkt 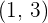 verläuft.
verläuft.
Bei diesem Problem müssen wir erneut den Fundamentalsatz der Analysis zur Lösung anwenden. Gegeben ist 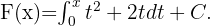 Wir nehmen den folgenden Wert für die Konstante
Wir nehmen den folgenden Wert für die Konstante  . Durch den Fundamentalsatz der Analysis erhalten wir nun
. Durch den Fundamentalsatz der Analysis erhalten wir nun

Wir integrieren in  und erhalten
und erhalten

Schließlich werten wir für  auf. Der Graph von
auf. Der Graph von  verläuft durch
verläuft durch 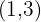 ,
,

Berechne die Gleichung des Graphen, der durch 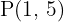 verläuft, und dessen Steigung an einem Punkt
verläuft, und dessen Steigung an einem Punkt 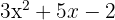 ist.
ist.
Wir erinnern uns, dass die Ableitung die Steigung der Funktion an einem bestimmten Punkt darstellt, so dass wir eine Stammfunktion der Funktion 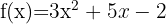 finden müssen. Gegeben ist
finden müssen. Gegeben ist  Das
Das  durch
durch 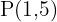 verlaufen muss, nehmen wir den folgenden Wert für die Konstante
verlaufen muss, nehmen wir den folgenden Wert für die Konstante 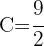 . Durch den Fundamentalsatz der Analysis erhalten wir nun
. Durch den Fundamentalsatz der Analysis erhalten wir nun
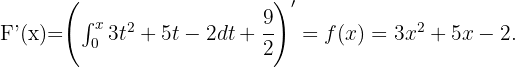
Wir integrieren in  und erhalten
und erhalten
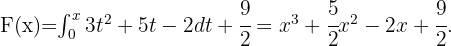
Schließlich werten wir für  aus und erhalten
aus und erhalten
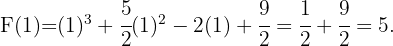
Die Antwort lautet
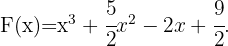
Ermittle die Stammfunktion der Funktion  , die für
, die für  null wird.
null wird.
Gegeben ist 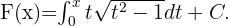 Wir nehmen den folgenden Wert für die Konstante
Wir nehmen den folgenden Wert für die Konstante  . Durch den Fundamentalsatz der Analysis erhalten wir nun
. Durch den Fundamentalsatz der Analysis erhalten wir nun

Wir integrieren in  und erhalten
und erhalten

Schließlich werten wir für  aus. Der Graph von
aus. Der Graph von  verläuft durch
verläuft durch 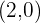 ,
,
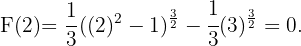
Die gesuchte Stammfunktion ist also wie folgt gegeben
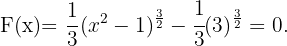
Mit KI zusammenfassen:












