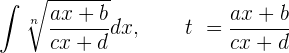Kapitel
Integrationsmethoden
Partielle Integration
Mit der Methode der partiellen Integration kann das Integral eines Produkts zweier Funktionen durch Anwendung der folgenden Formel berechnet werden:
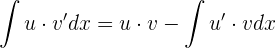
Bei gebrochen rationalen Integralen, bei denen Zähler und Nenner Polynome sind, geht man davon aus, dass der Grad des Zählers kleiner ist als der des Nenners, da er sonst dividiert werden würde.
Empfehlungen, die bei der Verwendung der partiellen Integration zu berücksichtigen sind:
- Logarithmusfunktionen werden als
gewählt.
- Trigonometrische Umkehrfunktionen (Arkussinus, Arkuskosinus, Arkustangens usw.) werden als gewählt.
- Polynome werden als gewählt.
- Exponentialfunktionen vom Typ Sinus und Kosinus werden als
gewählt.
- Trigonometrische Funktionen vom Typ Sinus und Kosinus werden als gewählt.
- Wenn wir partiell integrieren , haben wir ein Polynom vom Grad
. Wir nehmen es als und der Vorgang wird Male wiederholt. - Wenn wir ein Integral nur mit einem Logarithmus haben, integrieren wir partiell und nehmen:
. - Wenn wir ein Integral nur mit einer trigonometrischen Umkehrfunktion haben, integrieren wir partiell und nehmen: .
Integration durch Substitution oder Variablentausch
Die Methode der Integration durch Substitution oder Variablentausch beruht auf der Ableitung der Zusammensetzung von zwei Funktionen.
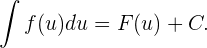
Wenn wir unseren Integranden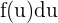 
als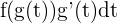 
ausdrücken können, wobei 
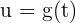, gilt:
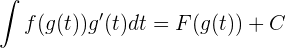
Um die Substitution durchzuführen, benennen wir einen Teil dessen, was integriert werden soll, mit einer neuen Variable 
, sodass sich ein einfacheres Integral ergibt.
Schritte für die Integration mit Substitution
1 Wir substituieren und differenzieren die zwei Terme:
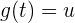
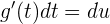
2 Wir ermitteln 
und setzen in das Integral und ein:
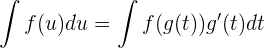
3Wenn das resultierende Integral einfacher ist, können wir integrieren:
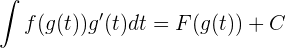
4 Wir kehren zur Ausgangsvariable zurück:
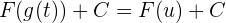
Häufig vorkommende Arten der Substitution
Bei rationalen Funktionen mit unterschiedlichen Wurzelexponenten, aber gleichem linearen Radikanden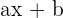 
, wird mit hoch das kleinste gemeinsame Vielfache der Wurzelexponenten substituiert.
Rationale Integrale
Rationale Integrale haben die Form
,
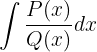wobei 
und 
Polynome sind.
Sobald wir wissen, dass der Nenner einen höheren Grad als der Zähler hat, zerlegen wir den Nenner in Faktoren.
Abhängig von den Nullstellen des Nenners gibt es die folgenden Arten von rationalen Integralen:
Fall 1: Rationale Integrale mit einfachen reellen Nullstellen
Der Bruch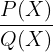 
kann wie folgt geschrieben werden:
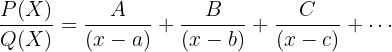
Die Koeffizienten 
, 
und 
sind Zahlen, die man erhält, indem man Koeffizienten addiert und bestimmt oder 
Werte zuweist.
Beispiel
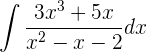
1 Da der Grad des Nenners nicht höher ist als der des Zählers, müssen wir zunächst eine Division durchführen, um diesen Bruch in die Summe eines Polynoms mit einem anderen Bruch umzuwandeln, dessen Nenner einen höheren Grad hat als der Zähler. Wenn wir die Polynome innerhalb des Integrals dividieren, ergibt sich
,
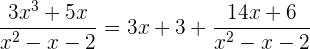2 weshalb wir unser Integral wie folgt schreiben können
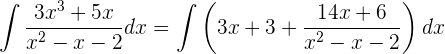
3 Der Nenner des Bruchs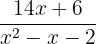 
hat einen höheren Grad als der Zähler. Wir können den Nenner faktorisieren 
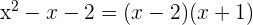und somit
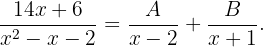
4 Wir addieren, um die Werte für und zu erhalten:
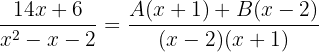
5 Da die beiden Brüche denselben Nenner haben, müssen auch die Zähler gleich sein:
6 Wir berechnen die Koeffizienten von , und . So erhalten wir die Werte für , für die der Nenner 0 wird.
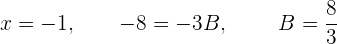
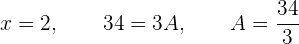
7 Schließlich können wir unser Integral wie folgt ausdrücken
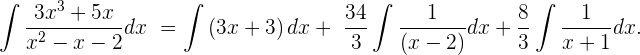
8 Wir stellen fest, dass es sich um Summen von Integralen handelt, die leichter zu lösen sind, wobei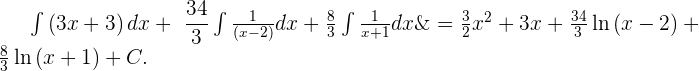 
9 Oder, in Bezug auf unser ursprüngliches Integral
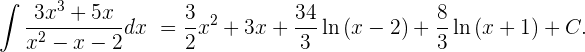
Fall 2: Rationale Integralle mit mehrfachen reellen Nullstellen
Der Bruch 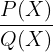, bei dem Mal den Faktor 
hat, kann wie folgt geschrieben werden:
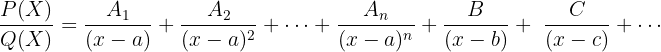
Beispiel
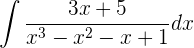
1 Wir stellen fest, dass der Nenner als Produkt geschrieben werden kann
2 Wir können den Bruch also wie folgt ausdrücken
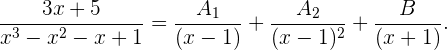
3 Wir addieren und erhalten
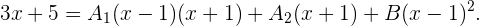
4 Um die Werte von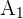 
, 
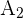und zu berechnen, weisen wir die Werte zu, für die der Nenner 0 wird:
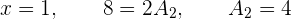
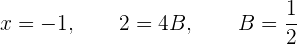
5 Wir können unser Integral wie folgt schreiben
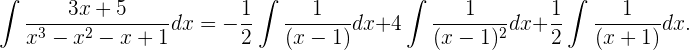
6 Dies ist eine Summe von einfacheren Integralen, deren Ergebnis wie folgt ist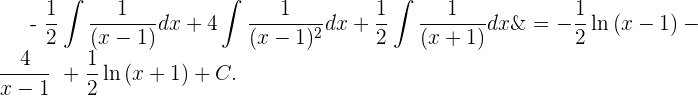 
7 Oder, in Bezug auf unser ursprüngliches Integral
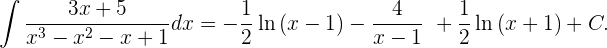
Fall 3: Rationale Integrale mit einfachen komplexen Nullstellen
Der Bruch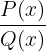 
, bei dem eine komplexe Nullstelle (also eine Nullstelle, die nicht in einfachen reellen Faktoren ausgedrückt werden kann) hat, kann wie folgt geschrieben werden:
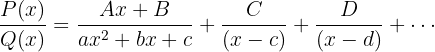
Dieses Integral wird in die Summe aus Integralen vom Typ "Logarithmus" und "trigonometrische Umkehrfunktion" zerlegt.
Beispiel
1 Wir können den Nenner als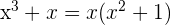 
faktorisieren. Wir können 
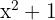nicht weiter in das Produkt der reellen einfachen Faktoren zerlegen, also belassen wir es bei einem Faktor vom Grad 2. Somit
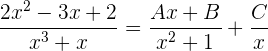
2 Wir addieren und erhalten
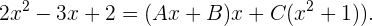
3 Wir ermitteln die Koeffizienten, indem wir die entsprechenden Rechenschritte durchführen und die Koeffizienten gleichsetzen:
4 Wir erhalten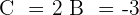 
5 Außerdem
6 Und somit
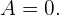
7 Wir schreiben unser Integral wie folgt
8 Dieses Integral ist nun einfacher und das Ergebnis ist
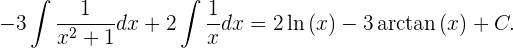
9 Oder, in Bezug auf unser ursprüngliches Integral
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
