Kapitel

Herleitung der Formel
Um ein Integral der Form
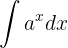
berechnen zu können, müssen wir beachten, dass die Ableitung einer Exponentialfunktion wie folgt gegeben ist

Daher wird das Integral von 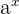 wie folgt berechnet:
wie folgt berechnet:

Somit kommen wir zu dem Schluss, dass die Integralformel für 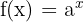 lautet:
lautet:

Für den speziellen Fall, dass  (Eulersche Zahl) ist, haben wir
(Eulersche Zahl) ist, haben wir
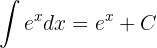
Schließlich gilt für eine Funktion  die folgende Substitutionsformel:
die folgende Substitutionsformel:

Und wenn die Basis  ist, haben wir
ist, haben wir

Wir stellen fest, dass 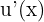 mit dem Differential multipliziert werden muss.
mit dem Differential multipliziert werden muss.
Beispiele
Berechne das folgende Integral
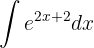
Wir stellen fest, dass die Basis der Exponentialfunktion  ist. Somit müssen wir
ist. Somit müssen wir 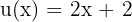 berechnen. Da
berechnen. Da 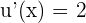 , müssen wir das Differential mit 2 multiplizieren:
, müssen wir das Differential mit 2 multiplizieren:
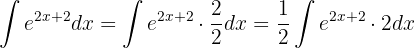
Damit können wir bereits das Integral berechnen:
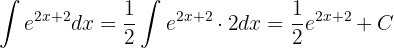
Berechne das folgende Integral
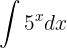
Wir stellen fest, dass die Basis 5 ist. Außerdem ist das Argument der Exponentialfunktion ganz einfach  . Somit können wir die Formel direkt mit
. Somit können wir die Formel direkt mit  anwenden:
anwenden:
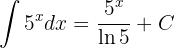
Berechne das folgende Integral des Produkts der Exponentialfunktionen:
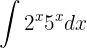
Wir beachten, dass  da sie denselben Exponenten haben. Das Integral wird also wie folgt berechnet
da sie denselben Exponenten haben. Das Integral wird also wie folgt berechnet
Es ist wichtig zu beachten, dass man zwar mithilfe der Methode der partiellen Integration zum gleichen Ergebnis gelangen könnte, das Verfahren jedoch mühsamer wäre.
Berechne das folgende Integral
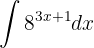
Wir stellen fest, dass 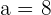 und
und  . Somit müssen wir
. Somit müssen wir  nehmen. Wir multiplizieren also das Differential mit 3 (gleichzeitig muss durch 3 geteilt werden, damit die Funktion dieselbe bleibt):
nehmen. Wir multiplizieren also das Differential mit 3 (gleichzeitig muss durch 3 geteilt werden, damit die Funktion dieselbe bleibt):
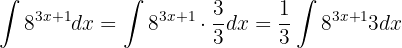
Das Integral lautet also
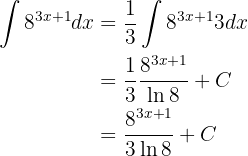
Berechne das folgende Integral
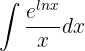
Es gibt zwei Möglichkeiten, diese Integralrechnung zu lösen. Am einfachsten ist es, 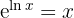 zu nehmen:
zu nehmen:
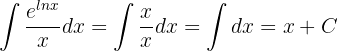
Die Definitionsmenge von 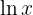 ist
ist 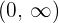 . Die Lösung ist daher ebenfalls auf diese Definitionsmenge beschränkt.
. Die Lösung ist daher ebenfalls auf diese Definitionsmenge beschränkt.
Da wir jedoch die Formel der Integralexponentialfunktion verwenden, können wir diese auch anwenden und sollten zum gleichen Ergebnis kommen. In diesem Fall beachten wir, dass  . Und somit ist
. Und somit ist  (was bereits mit dem Differential multipliziert wird), das heißt,
(was bereits mit dem Differential multipliziert wird), das heißt,
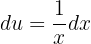
Und somit
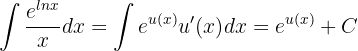
Aber da  , haben wir
, haben wir
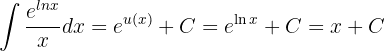 ,
,
da 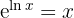 .
.
Berechne das folgende Integral

Wir stellen fest, dass  . Somit
. Somit
 ,
,
was bereits mit dem Differential multipliziert ist. Daher
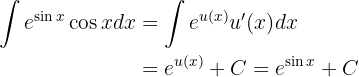
Berechne das folgende Integral

Wir stellen fest, dass 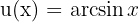 . Daher ist dieses Integral recht einfach, wenn wir uns daran erinnern, dass
. Daher ist dieses Integral recht einfach, wenn wir uns daran erinnern, dass
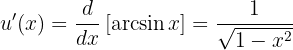
Das Integral lautet also
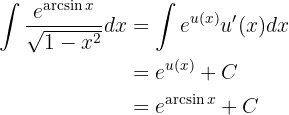
Mit KI zusammenfassen:












