Kapitel
Substitution
Die Methode der Substitution oder des Variablentauschs basiert auf der Ableitung der zusammengesetzten Funktion.
Um die Variable zu tauschen, benennen wir einen Teil dessen, was integriert werden soll, mit einer neuen Variable t, so dass ein einfacheres Integral entsteht.
Schritte der Integration durch Substitution
1 Der Variablentausch oder Substitution wird durchgeführt und es wird zwischen 2 Ausdrücken unterschieden:
2 Das Differential wird durch das Integral ersetzt:
3 Wenn das resultierende Integral einfacher ist, integrieren wir:
4 Rückkehr zur Ausgangsvariablen:
Beispiel: Löse das Integral mit der Substitution
1 Wir tauschen die Variable
Wir berechnen das Differential
2Wir setzen in das Integral ein und vereinfachen
3 Wir lösen das neue Integral
4 Wir kehren zur Ausgangsvariable zurück: 
Unsere gesuchte Lösung ist
Beispiele für die Substitution
Wir sehen uns im Folgenden einige Beispiele für die Methode der Substitution an
1 
2 
3 
4 
5 Bei Wurzelfunktionen mit unterschiedlichen Wurzelexponenten, die aber denselben linearen Radikanden 
haben, ist der Variablentausch 
hoch das kleinste gemeinsame Vielfache der Wurzelexponenten.
6 Wenn 
gerade ist:
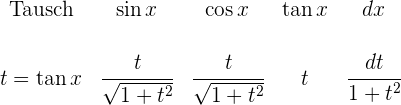
7 Wenn 
ungerade ist:
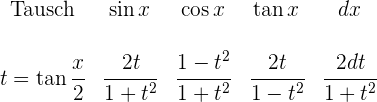
Aufgaben
Löse folgende Integrale mit der Methode der Substitution.
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und wenden zur Vereinfachung Winkelfunktionen an
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück und bestimmen hierfür
Wir berechnen den Sinus und den Kosinus für
Das Ergebnis mit der Variablen 
:
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und vereinfachen
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und vereinfachen
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und vereinfachen
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück
Die Lösung in Bezug auf die Ausgangsvariable lautet also
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und vereinfachen
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück
Die Lösung in Bezug auf die Ausgangsvariable lautet also
1 Wir substituieren und berechnen das Differential
2 Wir setzen in das Integral ein und vereinfachen
3 Wir lösen die resultierenden Integrale
4 Wir kehren zur Ausgangsvariable zurück
Die Lösung in Bezug auf die Ausgangsvariable lautet also
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
