Willkommen bei unserem Blog, der sich mit der faszinierenden und effektiven mathematischen Technik der "partiellen Integration" beschäftigt. Integrale sind ein grundlegender Bestandteil der Infinitesimalrechnung und können in vielen Fällen eine Herausforderung darstellen. Aber keine Angst! Wir sind hier, um das Geheimnis der partiellen Intgration zu lüften und sie leichter verständlich zu machen.
Von der Physik über das Ingenieurwesen bis hin zu verschiedenen Wissensgebieten tauchen immer wieder Funktionen auf, die mithilfe der partiellen Integration integriert werden müssen. In diesem Artikel stellen wir dir eine Reihe von Aufgaben mit Lösungen vor, die dir helfen werden, dieses wichtige mathematische Verfahren zu verstehen und zu perfektionieren.
Schließe dich uns an und werde Profi in der partiellen Integration!
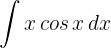
1 Wir wählen  aus und berechnen
aus und berechnen  sowie
sowie 

2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein

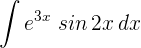
1 Wir wählen 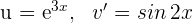 aus und berechnen
aus und berechnen  sowie
sowie 

2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
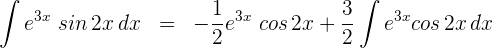
3 Das letzte erhaltene Integral wird durch die partielle Integration gelöst, daher wählen wir 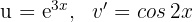 und berechnen
und berechnen  sowie
sowie 
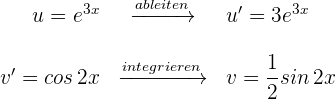
4 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und erhalten
in die Formel der partiellen Integration ein und erhalten
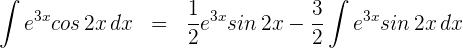
5 Wir setzen das in Schritt 4 erhaltene Ergebnis in das Ergebnis von Schritt 2 ein und lösen die sich daraus ergebende Gleichung
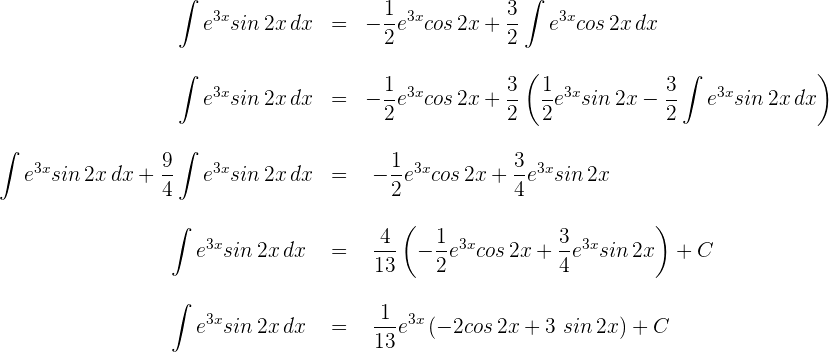
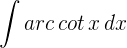
1 Wir wählen 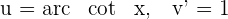 aus und berechnen
aus und berechnen  sowie
sowie 
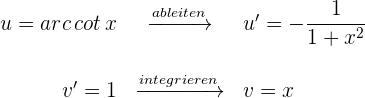
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
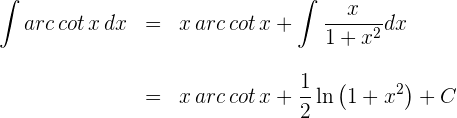
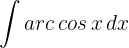
1 Wir wählen  aus und berechnen
aus und berechnen  sowie
sowie 
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein

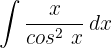
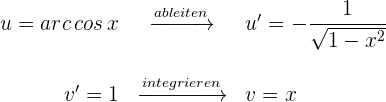
1 Wir wählen 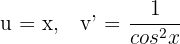 aus und berechnen
aus und berechnen  sowie
sowie 

2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und berücksichtigen dabei
in die Formel der partiellen Integration ein und berücksichtigen dabei 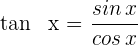
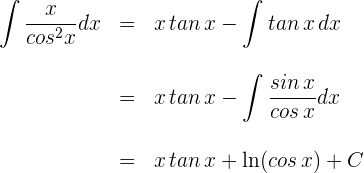
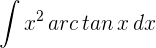
1 Wir wählen 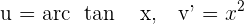 aus und berechnen
aus und berechnen  sowie
sowie 
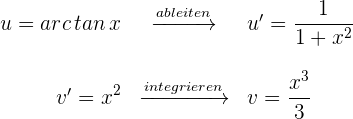
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
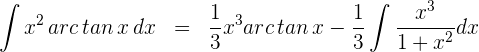
3 Wir führen die Division des neuen Integranden durch und erhalten

4 Wir setzen in das Integral ein und lösen


1 Wir wählen 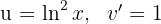 aus und berechnen
aus und berechnen  sowie
sowie 
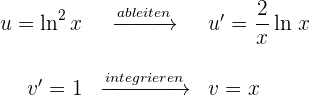
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein

3 Das letzte erhaltene Integral wird mittels der partiellen Integration gelöst. Deshalb wählen wir 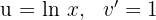 und berechnen
und berechnen  sowie
sowie 
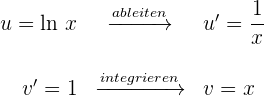
4 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und erhalten
in die Formel der partiellen Integration ein und erhalten

5 Wir setzen das in Schritt 4 erhaltene Ergebnis in das Ergebnis von Schritt 2 ein.


1 Wir wählen 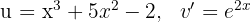 aus und berechnen
aus und berechnen  sowie
sowie 
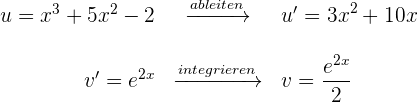
2 Wir setzen die Werte  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
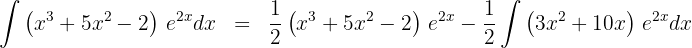
3 Das letzte erhaltene Integral wird mittels der partiellen Integration gelöst. Deshalb wählen wir 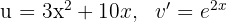 und berechnen
und berechnen  sowie
sowie 
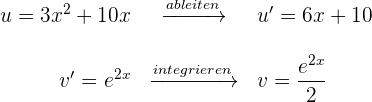
4 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und erhalten
in die Formel der partiellen Integration ein und erhalten
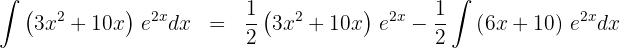
5 Das letzte erhaltene Integral wird mittels der partiellen Integration gelöst. Deshalb wählen wir 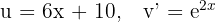 und berechnen
und berechnen  sowie
sowie 
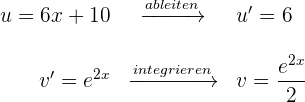
6 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und erhalten
in die Formel der partiellen Integration ein und erhalten
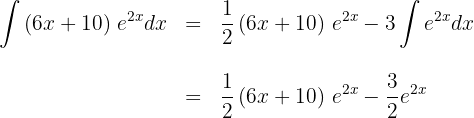
7 Wir setzen das Ergebnis von Schritt 6 in das Ergebnis von Schritt 4 ein

8 Wir setzen das Ergebnis von Schritt 7 in das Ergebnis von Schritt 2 ein
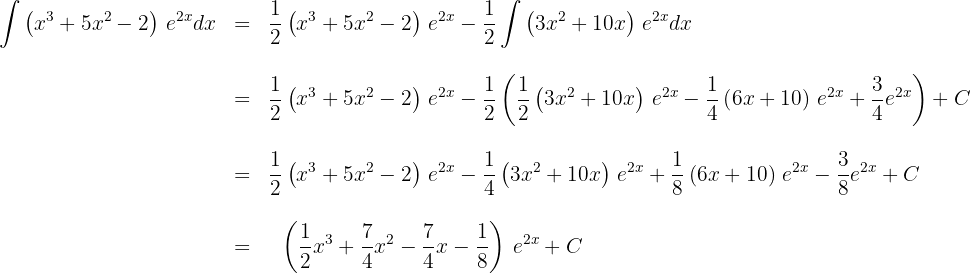
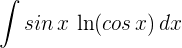
1 Wir wählen 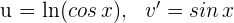 aus und berechnen
aus und berechnen  sowie
sowie 
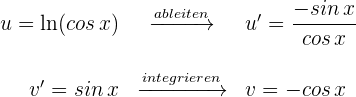
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
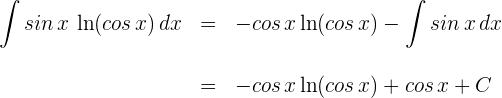
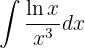
1 Wir wählen  aus und berechnen
aus und berechnen  sowie
sowie 
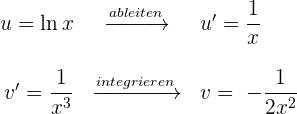
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
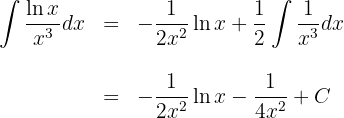
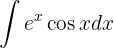
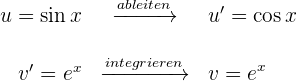
1 Wir wählen 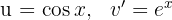 aus und berechnen
aus und berechnen  sowie
sowie 
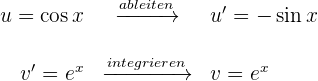
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
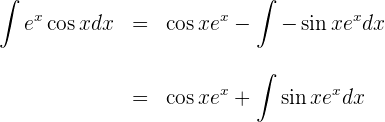
3 Das letzte erhaltene Integral wird mittels der partiellen Integration gelöst. Deshalb wählen wir 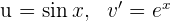 und berechnen
und berechnen  sowie
sowie 
4 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein und erhalten
in die Formel der partiellen Integration ein und erhalten
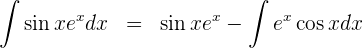
5 Wir setzen das Ergebnis von Schritt 4 in das Ergebnis von Schritt 2 ein und lösen die resultierende Gleichung
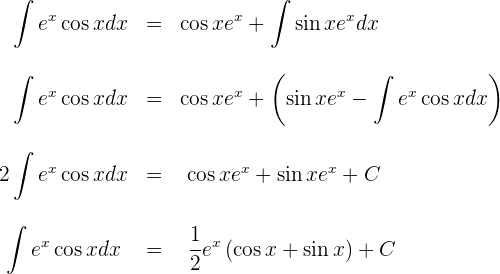
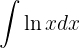
1 Wir wählen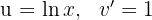 aus und berechnen
aus und berechnen  sowie
sowie 
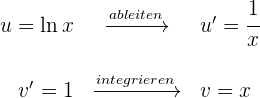
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
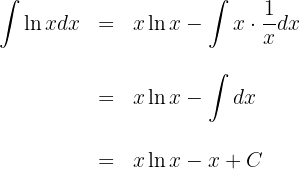
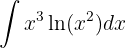
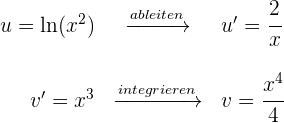
1 Wir wählen 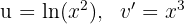 aus und berechnen
aus und berechnen  sowie
sowie 
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein

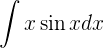
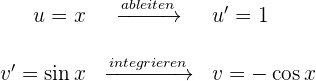
1 Wir wählen  aus und berechnen
aus und berechnen  sowie
sowie 
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
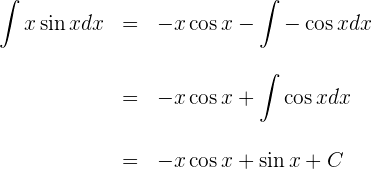

1 Wir wählen 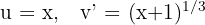 aus und berechnen
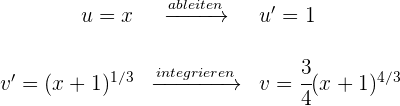
aus und berechnen  sowie
sowie 
2 Wir setzen die Werte für  und
und  in die Formel der partiellen Integration ein
in die Formel der partiellen Integration ein
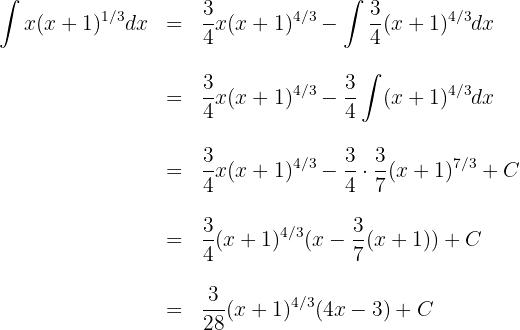
Mit KI zusammenfassen:



